从井字棋说起
很多人都玩过井字棋,下棋的时候怎么提高自己赢的概率呢?高手又是怎么下棋的呢?如何找到胜率更高的下法?
其实非常简单,不管是井字棋,还是象棋或者围棋,在下棋的时候,我们都会在脑海里进行模拟:
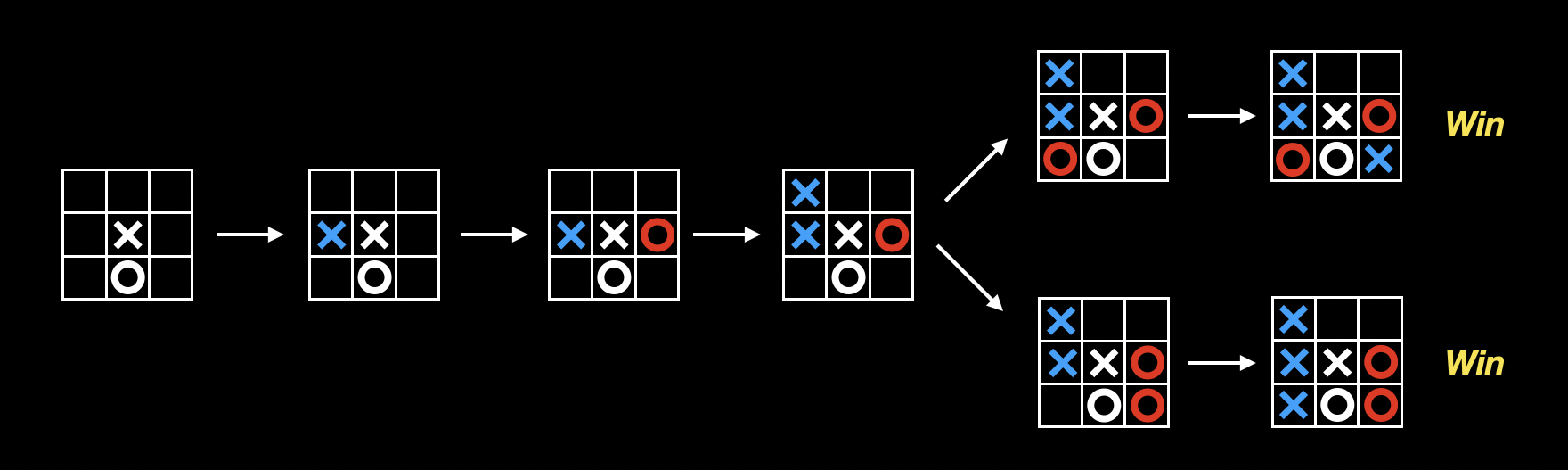
通过模拟,每走一步前,提前想好后面十步,以提高胜率。在井字棋中,甚至可以通过模拟来找到必胜走法(例如上图中的第一步)。
只要能穷举出所有可能的落子和棋局,我们就能算出每个棋局的胜率,从而选择胜率最高的下法:
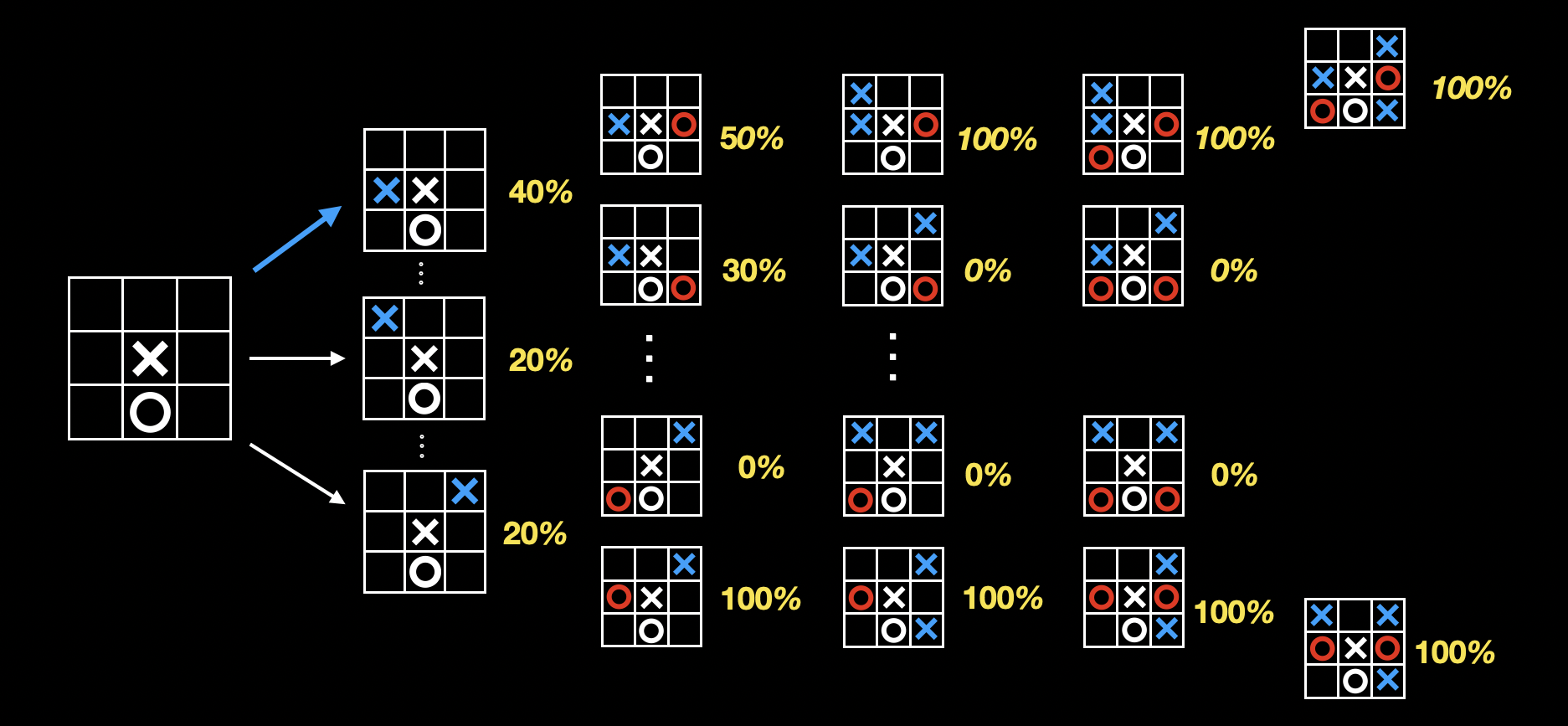
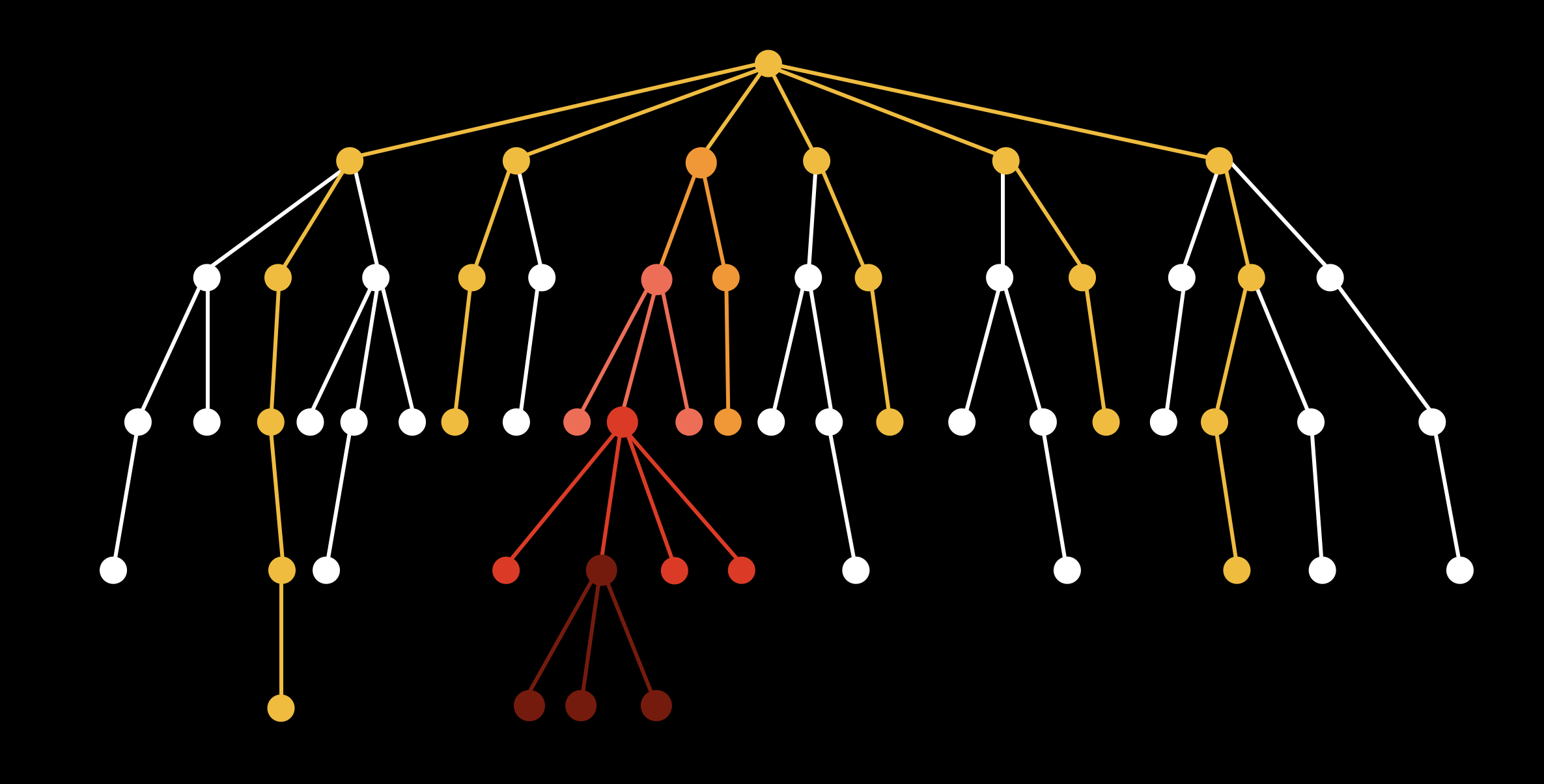
上图这棵从游戏初始状态开始延伸出所有状态节点的树,称为游戏树。游戏树的大小,反应了游戏的复杂度。
下棋是一个双方互相博弈的过程,我方可以选择当前胜算最高的落子,但对方的落子我方无法控制,因此这里需要介绍另一个算法:极小化极大搜索算法(Minimax Tree Search)。
极小化极大搜索
Minimax 的主要思路是,假定你和你的对手都是最聪明的,都选择走对各自来说最好的走法。算法很简单,首先我们通过穷举,计算出某一层节点我方胜算:
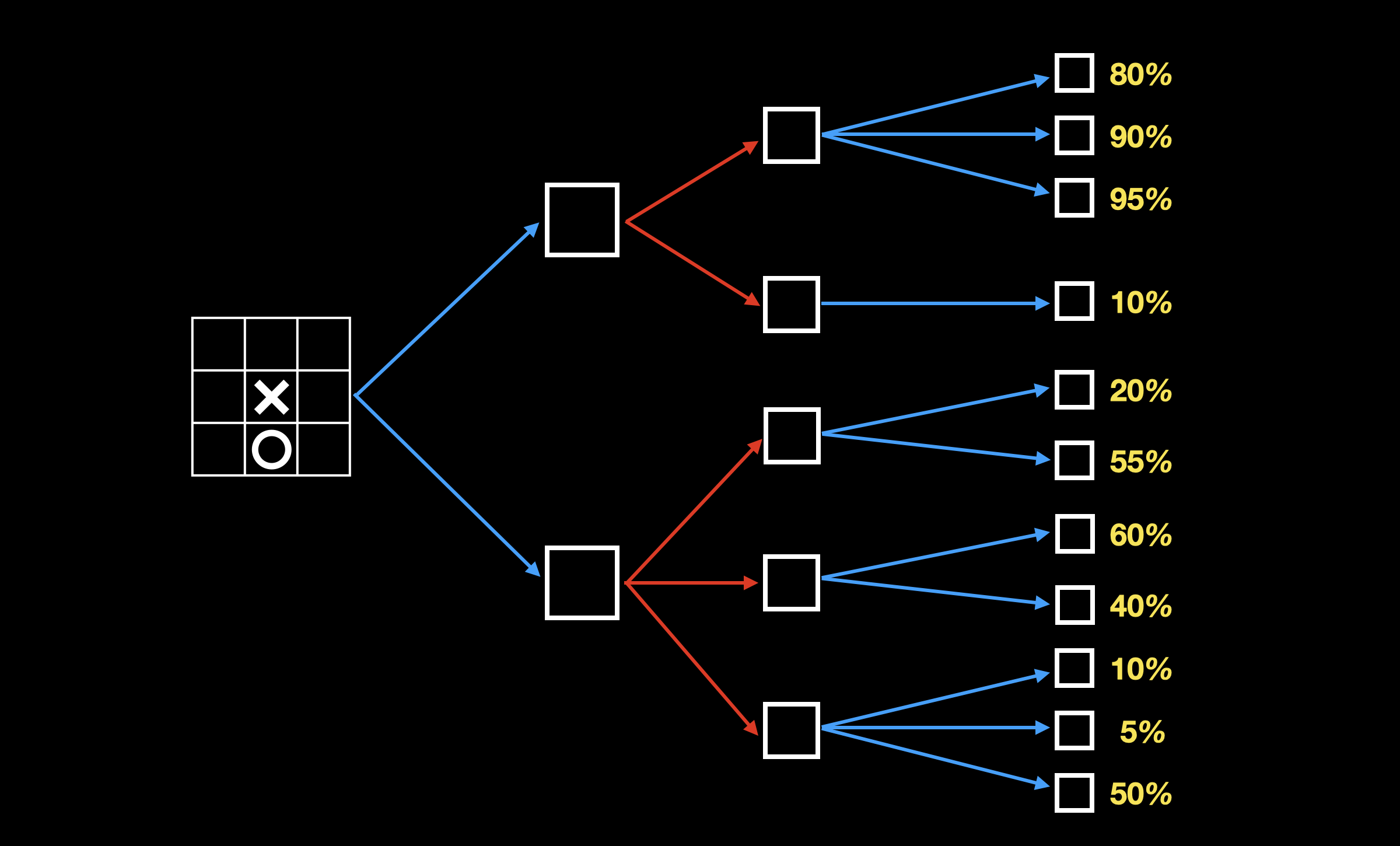
当我方选择落子时,选择我方胜算最高的分支(下图加粗):
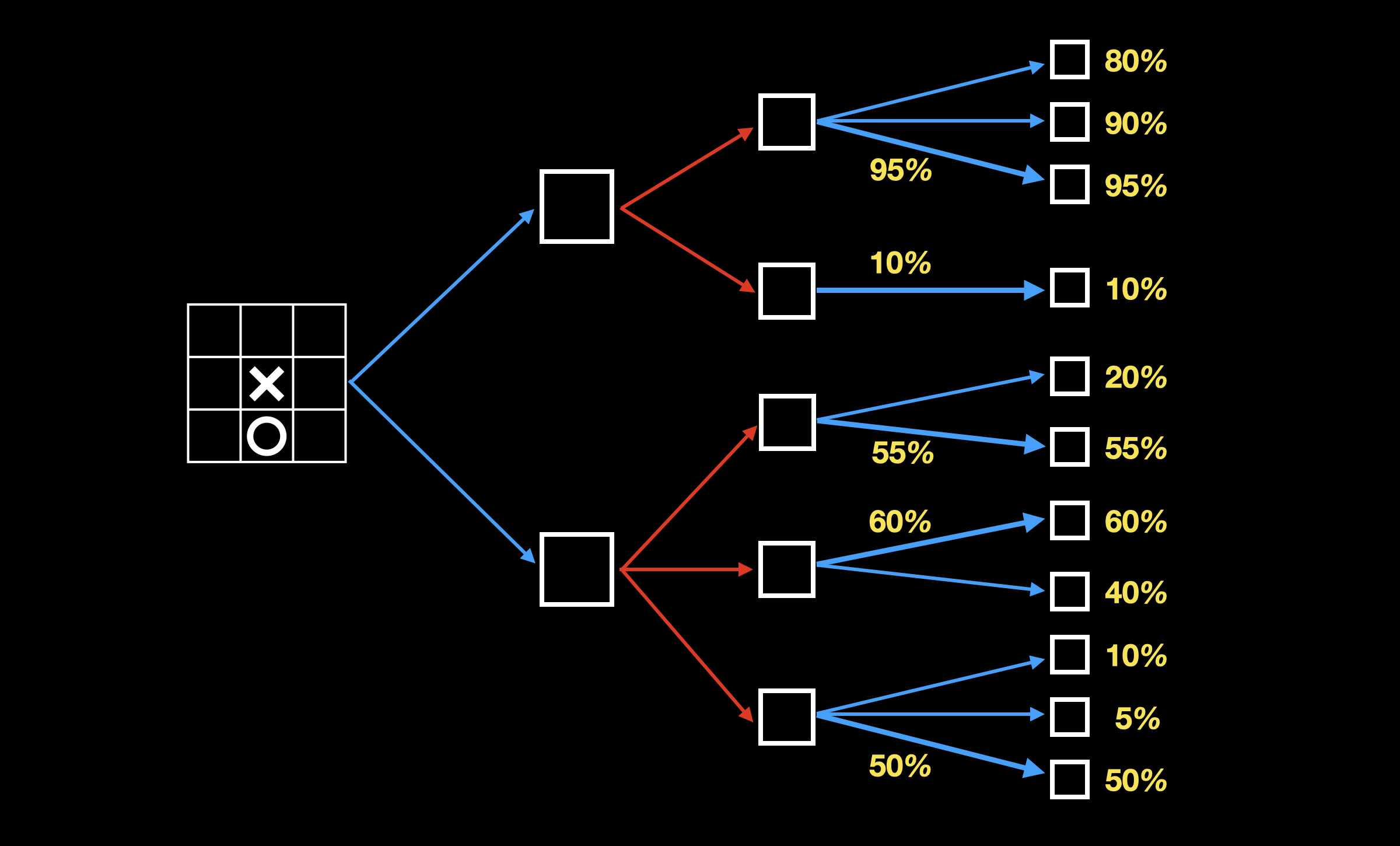
当对方选择落子时,选择我方胜算最低的分支(下图加粗):
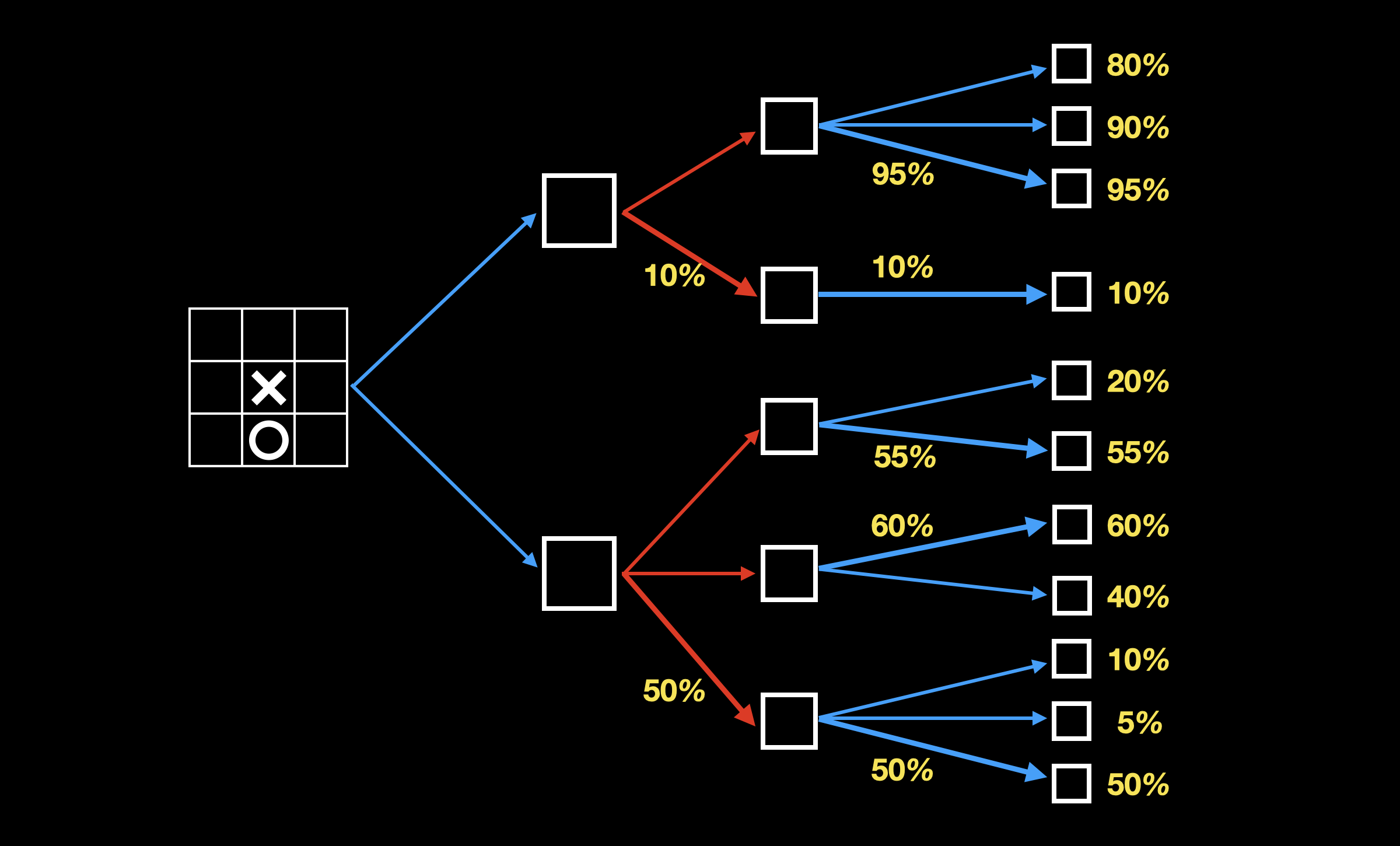
当我方再次选择落子时,选择我方胜算最高的分支(下图加粗):
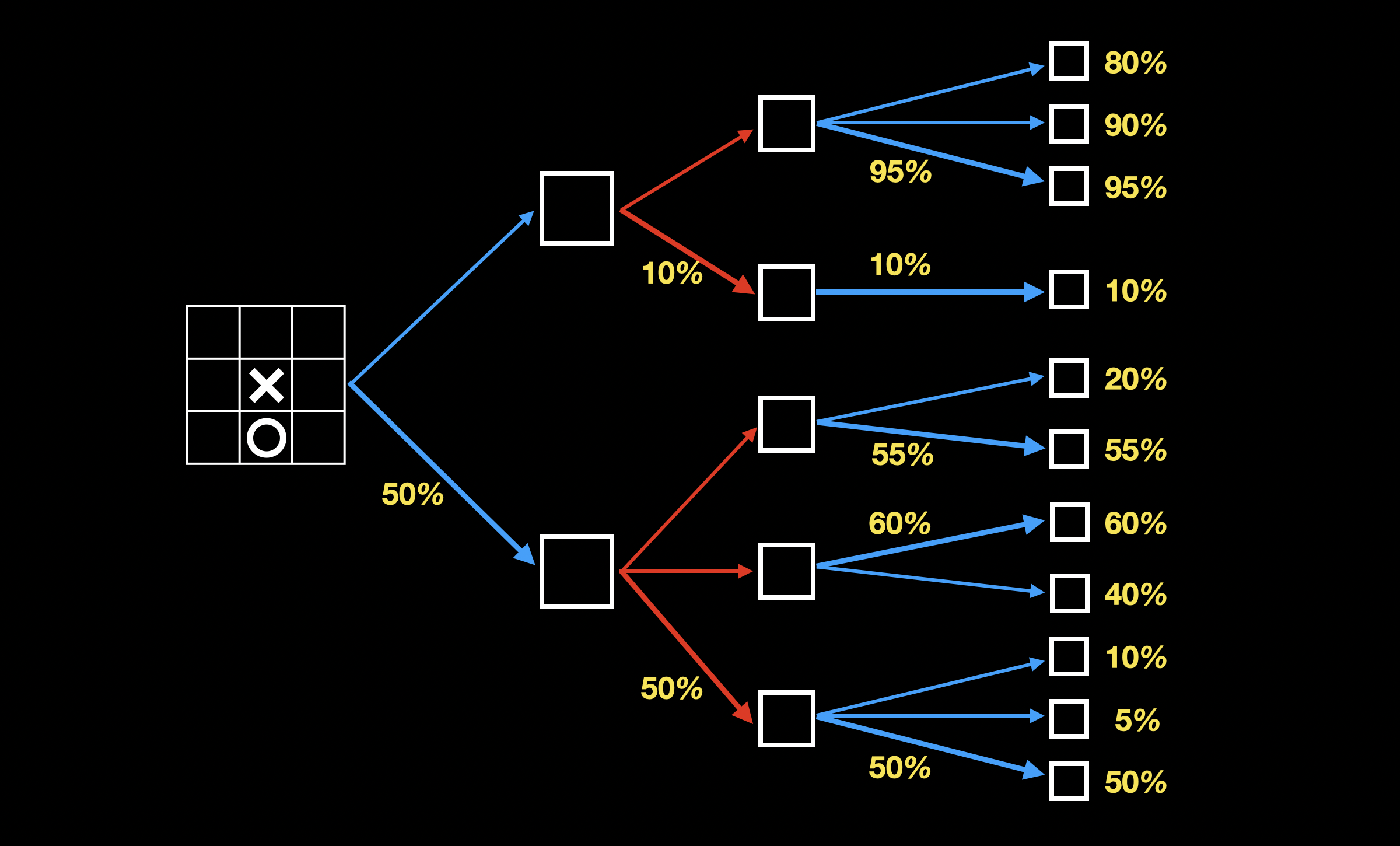
从叶子节点开始逐层往父节点推进,每一层都选择对自己最有利的走法,直到推进到根节点,即游戏的初始状态。通过 minimax 算法,构建完搜索树,我们找到了胜率最高的下棋方法。类似的,程序也能通过这个算法学会下棋。在 1997 年击败国际象棋世界冠军的“深蓝”,就基于 minimax 算法。为了减少树探索的深度,深蓝还引入了评估模块,通过不同棋子所处的不同位置来评估残局。
围棋
围棋不管从状态空间复杂度,还是游戏树大小上都远超过其他棋牌类游戏,无法穷举所有落子。并且对于残局的评估更加困难,因为围棋中每个棋子都相同,难以利用每个棋子的位置/数量/权重来评估当前局面。想攻克围棋 AI,就必须从想办法减少树探索的深度和广度。而蒙特卡洛树搜索,就是为了解决树探索空间巨大的问题。
蒙特卡洛树搜索
介绍蒙特卡洛树之前,先介绍蒙特卡洛方法。蒙特卡洛方法又称统计模拟法、随机抽样技术,是一类以概率和统计理论方法为基础的计算方法。简单的说就是通过多次采样来得到近似结果。
围棋的游戏树空间巨大,无法穷举,且难以通过简单的规则或公式来评估残局。蒙特卡洛树搜索采用多次采样来估测当前棋局和走法的好坏,从而“学习”如何下一盘好棋。
首先简单介绍下蒙特卡洛树搜索的流程:
- 第一阶段:我不知道该怎么下棋,我就随便下,直到下完一局,得到结果(胜或者负)
- 当我下了无数局后,通过统计,大概能知道,每个棋局状态我走哪一步胜算更高
- 根据得到的统计策略,我继续下无数局,下棋的时候优先选择我统计出来的胜算高的下法
- 随着下的局数越来越多,统计结果越来越接近真实的结果,也就找到最优的下法
大概知道原理后,接下来详细介绍下蒙特卡洛树搜索算法。蒙特卡洛树搜索分为四个阶段:选择(Selection)、扩展(Expansion)、评估(Evaluation)、回溯(Backup)。蒙特卡洛树中,每条边(表示行动,在下棋的场景下就是指落子)都保存一个 Q 值、N 值和 W 值。Q 值表示该行动的价值(走这步棋是好是坏),N 值表示采取该行动的次数(走这步棋的次数),W 值表示该行动的累积收益(走这一步棋后,总共输赢了多少局)。Q = W/N,初始值都为 0。这里我们以井字棋为例来讲解蒙特卡洛树算法。
选择
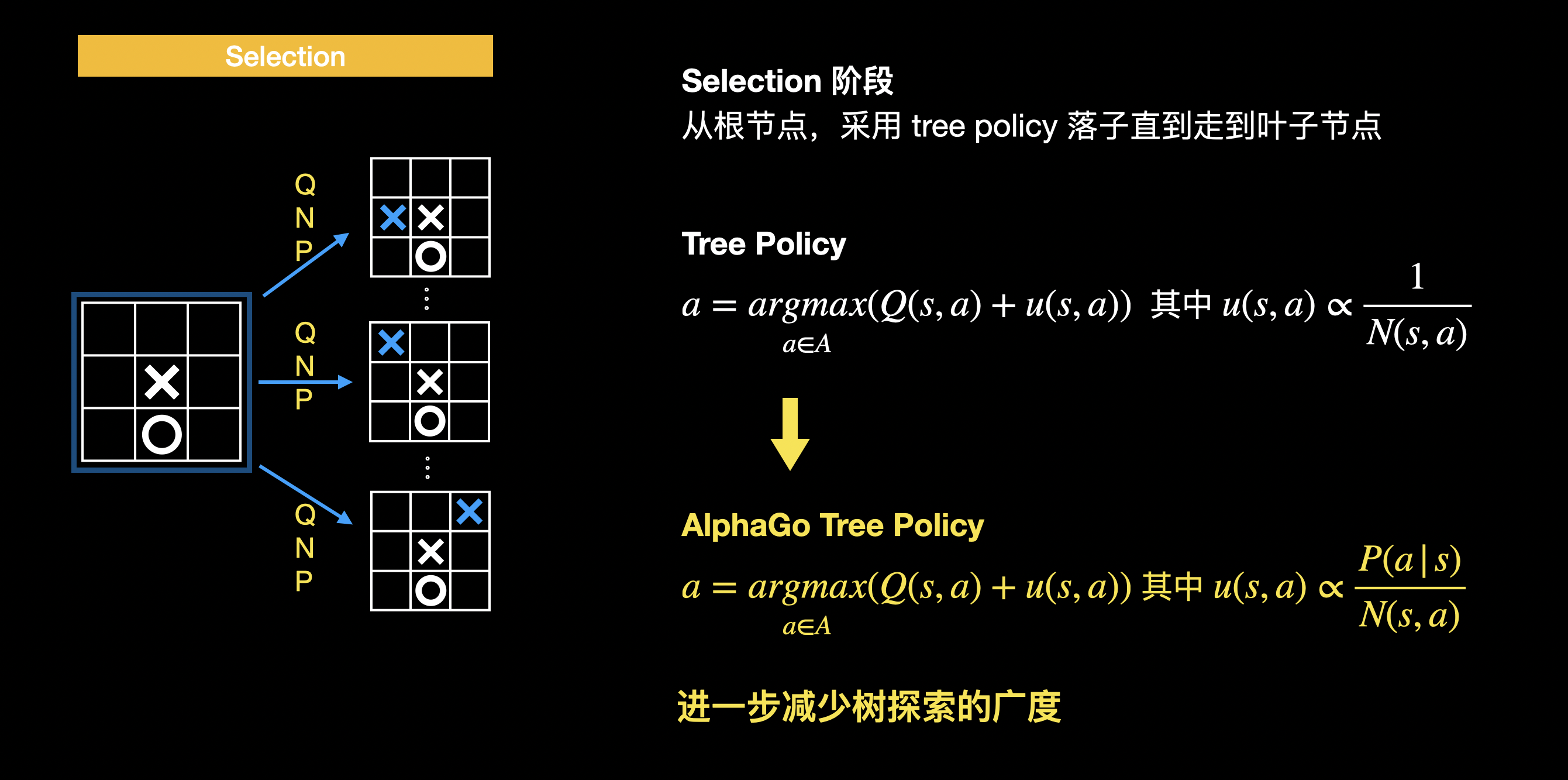
从根节点,通过 Tree Policy 进行落子,直到走到叶子节点:

因为 Q、N、W 初始值都是 0,因此一开始其实是随机落子。从 u 项可以看出 tree policy 会优先选择没走过的分支。 每次选择落子后,对应边的 N 值加 1 。随着模拟次数越来越多,u 项趋近于 0,这时 tree policy 会优先选择 Q 值最高(也即胜算最高)的落子。
评估
走到叶子节点时,通过评估叶子节点的价值(即当前棋局的胜算),来评估从开始到现在这系列落子是好是坏。评估的方法就是蒙特卡洛方法,通过随机模拟走完一次完整棋局(称为 rollout),得到胜负结果:
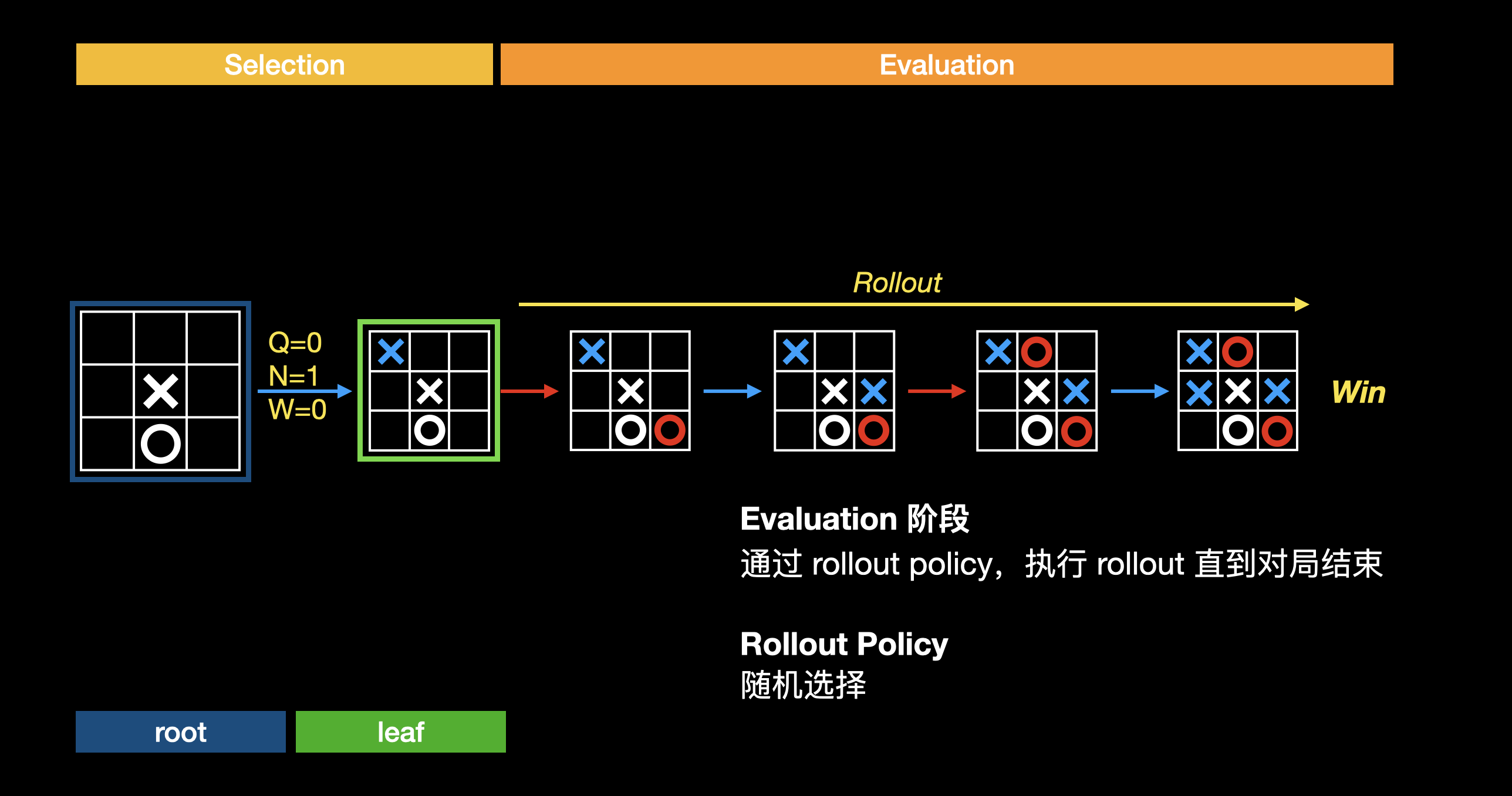
回溯
如果模拟完这局,我方胜利。意味着当前局面是有可能赢的,可以调高这系列走法的 Q 值。如果模拟结果是我方输了,则调低这一系列的走法的 Q 值。调整 Q 值的这个过程叫做回溯,将根节点走到当前叶子节点的路径上的所有边都根据输赢结果更新 Q 值:
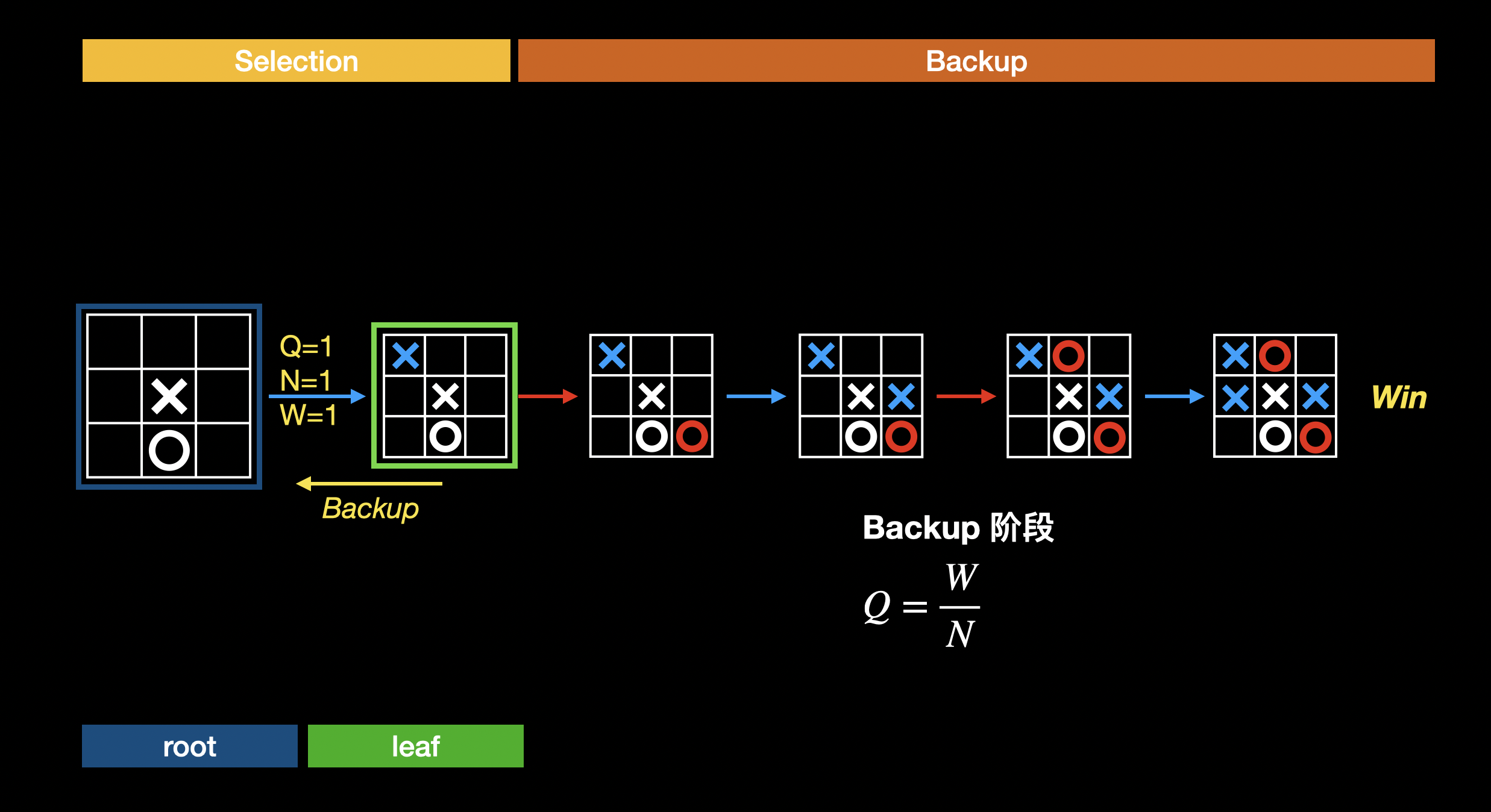
通过多次选择-评估-回溯的迭代,对叶子节点的评估(即对当前棋局的胜算评估)会越来越准确。相应的,Q 值也会逐渐接近真实的行动价值。
思考:回溯为什么只更新蒙特卡洛树节点的 Q 值?而不更新所有节点的 Q 值(包括在蒙特卡洛树之外的节点)?
答: 状态空间巨大。
扩展
目前为止,蒙特卡洛树和穷举似乎也没太多区别,通过无数次模拟去统计一个大致的胜率,树探索的广度和深度似乎并无太大区别。这其中关键在于蒙特卡洛树并不是完全随机模拟,而是会优先探索胜算更高的走法,从而减少树探索的广度(通过 Tree Policy)。因此如何去扩大蒙特卡洛树,使每一层都优先探索胜算更高的走法?这是通过扩展来实现的。当经过多次模拟,边访问次数 N 大于某个阈值时(N 越大,模拟的次数越多,意味着估算的 Q 值越精确),就可以对蒙特卡洛树进行扩展:
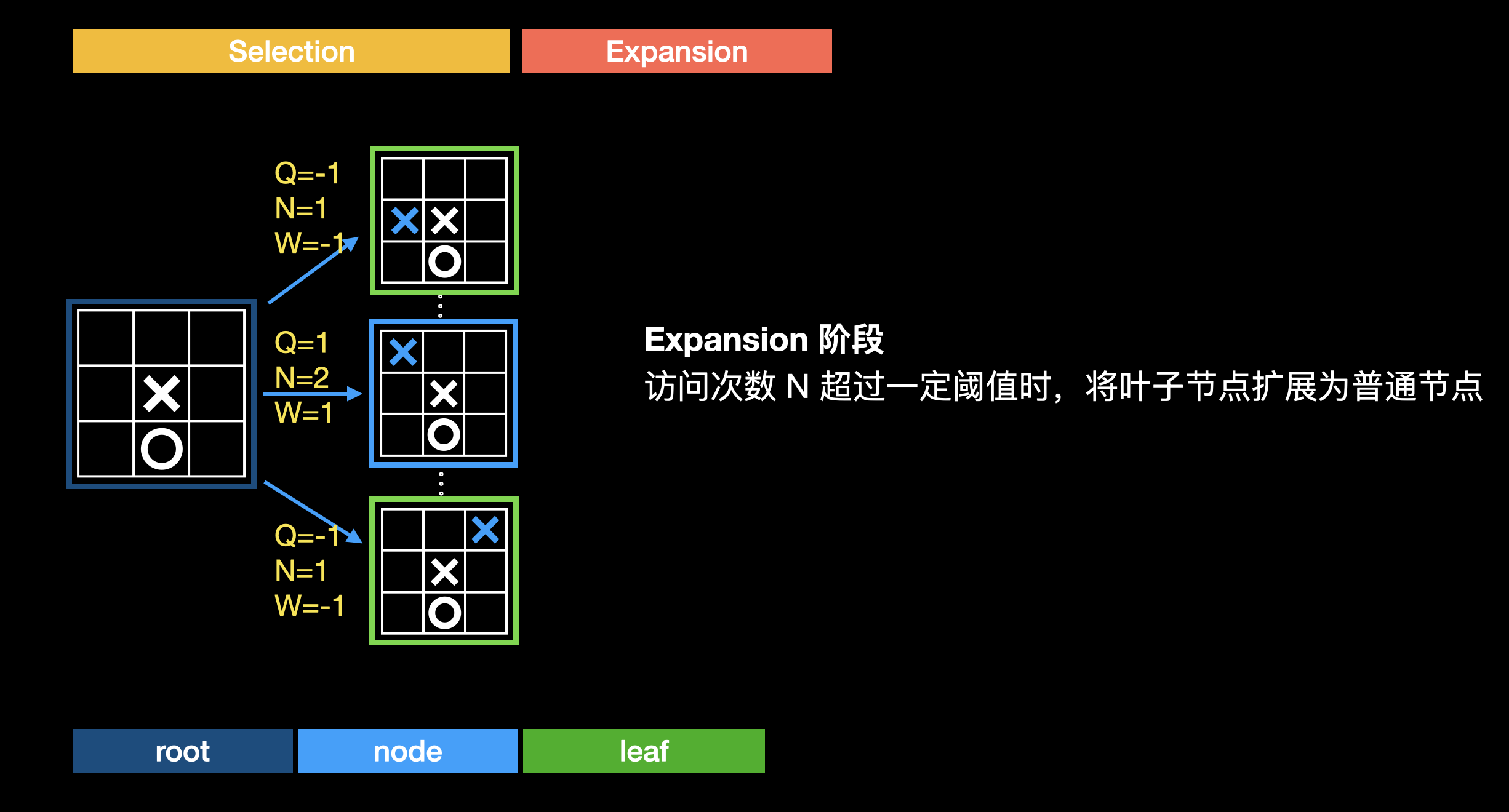
扩展使得蒙特卡洛树逐层扩大,进一步优先探索价值更高的分支,以减少探索的广度。
落子
选择→ (扩展)→ 评估 → 回溯称为一次迭代。当模拟完多次迭代后,意味着对行动价值的评估比较准确了,就可以进行真正的落子。注意,选择、扩展、评估和回溯都只是模拟的过程。落子有两种策略,一种是选择 Q 值最大的边,一种是选择 N 值最大的边。
落子之后,等待对方落子,蒙特卡洛树向下推进,从新的根节点开始,继续进行选择→ (扩展)→ 评估 → 回溯的迭代:
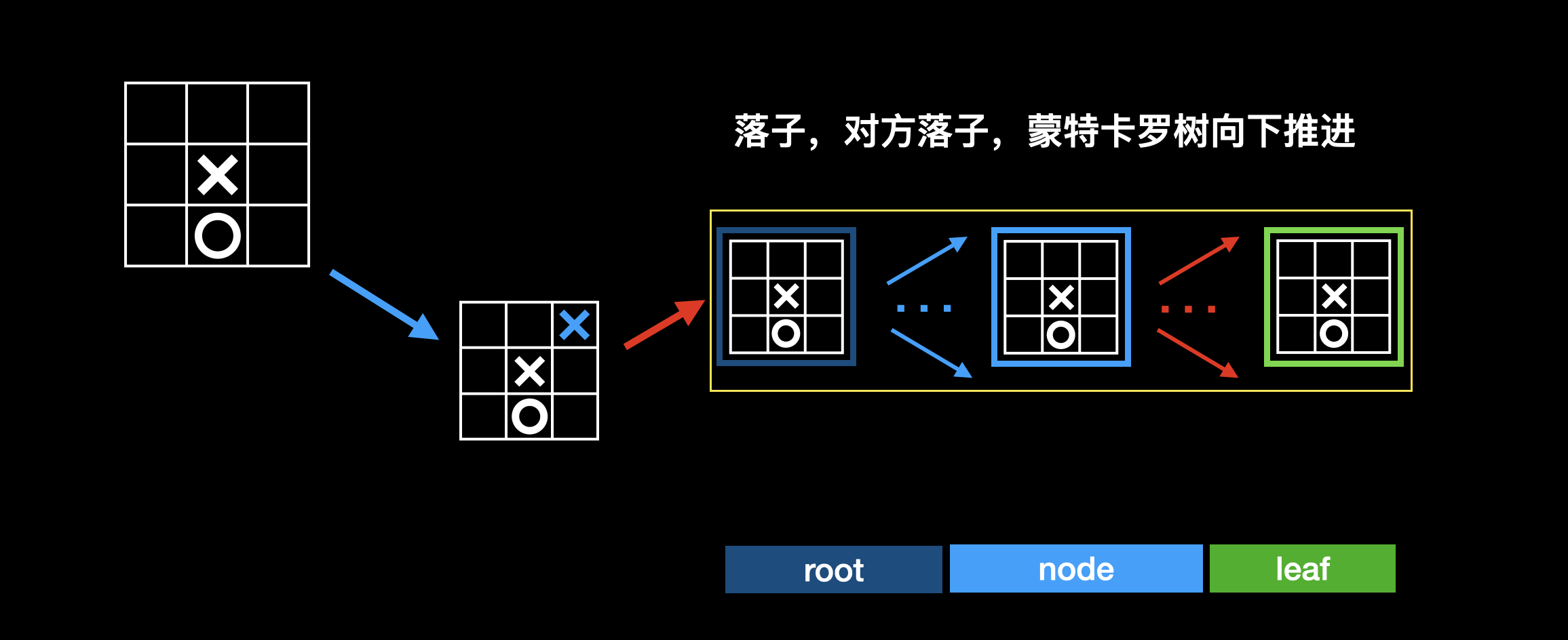
总结
蒙特卡洛树以当前棋局状态为根节点,通过多次模拟完整棋局来估算落子好坏,以选择最佳落子策略。迭代中优先探索价值更高的节点,以减少搜索的广度。同时评估叶子节点价值的时候,采用随机模拟的方式进行估算,也减少了深度搜索的次数(无需穷尽搜索所有子节点)。
思考
在选择阶段,Q 和 N 的初始值都是 0,因此只能进行随机落子。如果可以更有选择性的进行落子,就能进一步减少探索的广度。
在评估阶段,如果可以对残局直接进行价值评估,就可以省去 rollout 的过程,减少了树搜索的深度。另一方面,蒙特卡洛树搜索 rollout 的过程中其落子策略是完全随机的,如果可以进行更有依据的落子策略,多次模拟估算的价值也会更加准确。
而 AlphaGo,就是在蒙特卡洛树搜索的基础上,做了这些优化。
AlphaGo
AlphaGo 同样基于蒙特卡洛树搜索,不同的是,在选择阶段会模仿人类的落子策略:
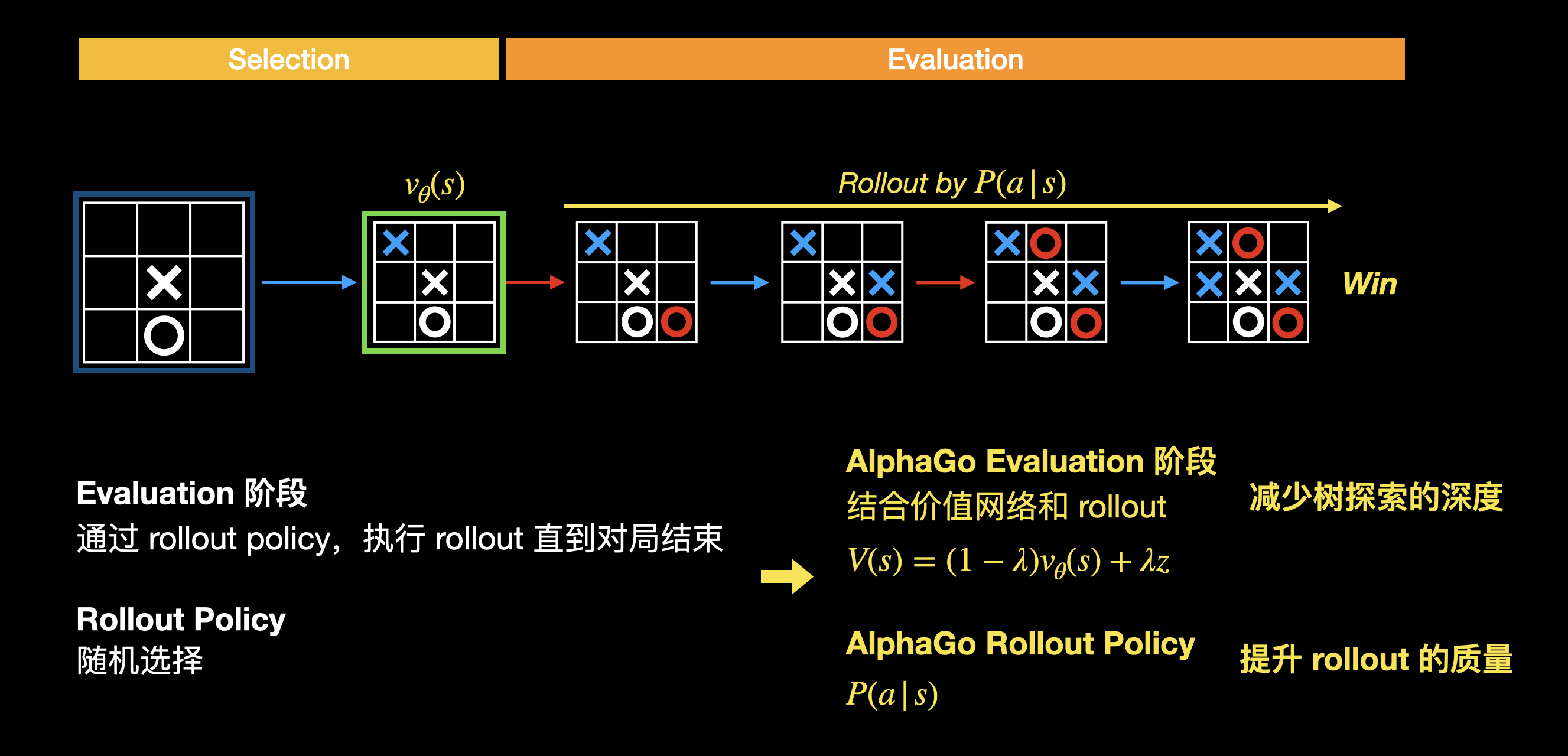
在评估阶段,会结合 rollout 和价值网络,来评估当前棋局的好坏。同样的,rollout 过程中的落子会模仿人类的落子策略:
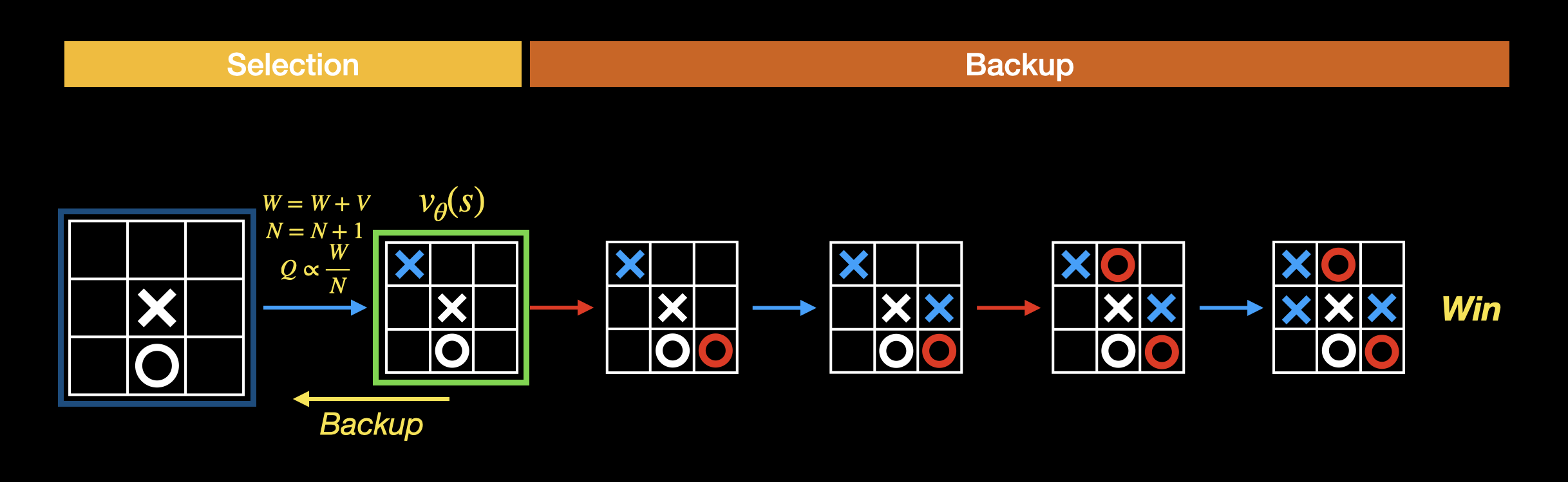
回溯阶段,采用结合 rollout 和价值网络的评估值进行回溯:
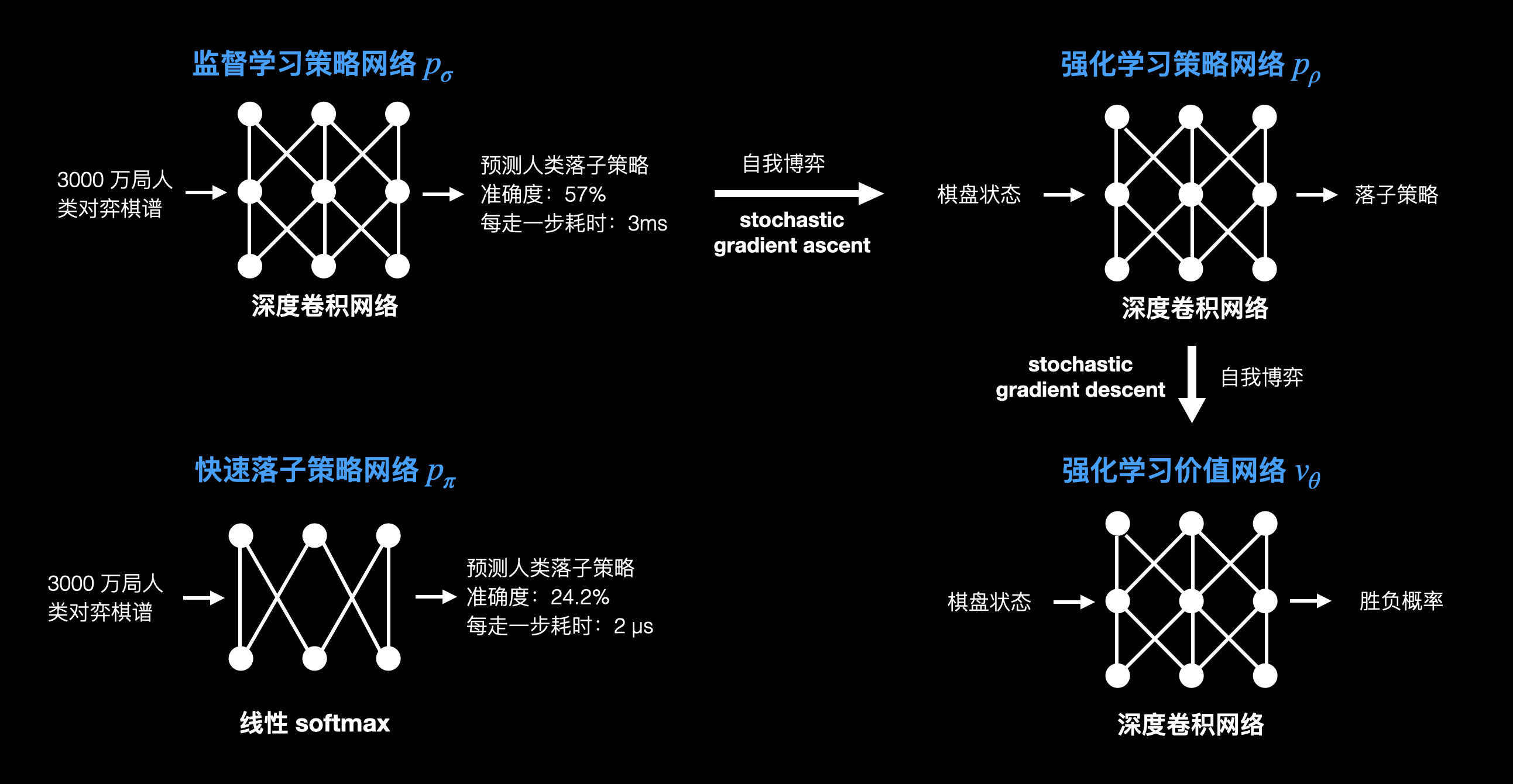
这就是 AlphaGo 对蒙特卡洛树搜索所做的优化。为了实现优化,首先,AlphaGo 需要学习人类的落子策略,即学习人类是如何下棋的。AlphaGo 训练了一个监督学习策略网络,输入为 3000 万人类对弈棋谱,训练模型为深度卷积网络,输出则是落子策略。另外 AlphaGo 还训练了一个速度更快,但准确度较低的快速落子策略网络。
训练出监督学习策略网络后,用该策略网络进行自我博弈,训练出一个强化学习策略网络。和监督学习策略网络不同的是,监督学习策略网络的目标是模仿人类落子,强化学习策略网络的目标是提高胜率。通过监督学习网络自我博弈训练出强化学习策略网络后,再用强化学习策略网络进行自我博弈,所产出的更高质量的自我博弈数据,被用来训练强化学习价值网络。强化学习价值网络的目标是预测棋局的价值,即当前棋局的胜算。
这四个网络的训练流程如下:
在训练出这四个网络之后,来看看 AlphaGo 版本的蒙特卡洛树搜索算法。
选择
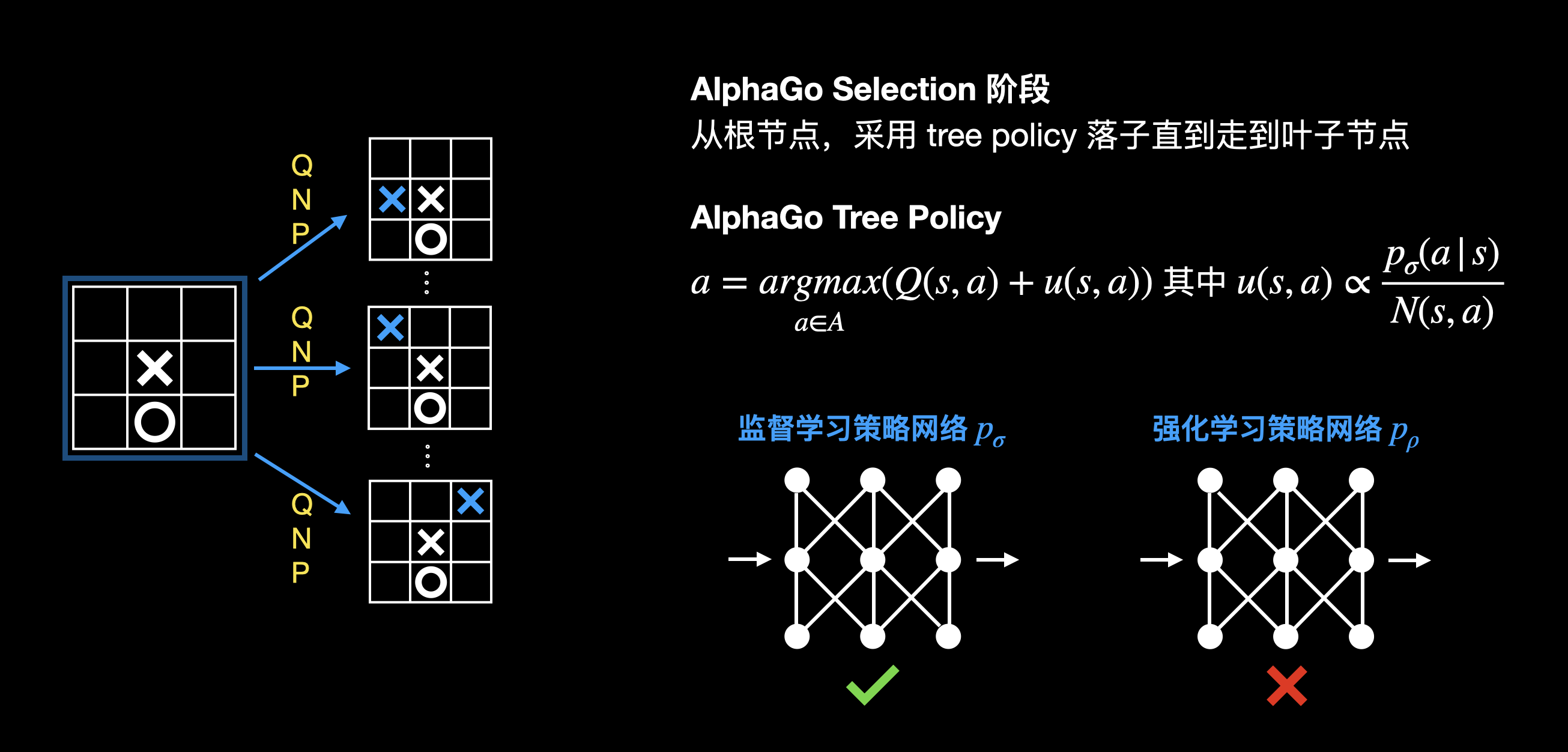
注意这里采用的是监督学习策略网络。为什么不用强化学习策略网络呢?论文提到是因为强化学习策略网络输出的落子策略相对单一(强化学习策略网络的目标是寻找最佳落子策略),效果没有监督学习网络的好(监督学习网络输出的落子策略比较发散)。
评估 & 回溯
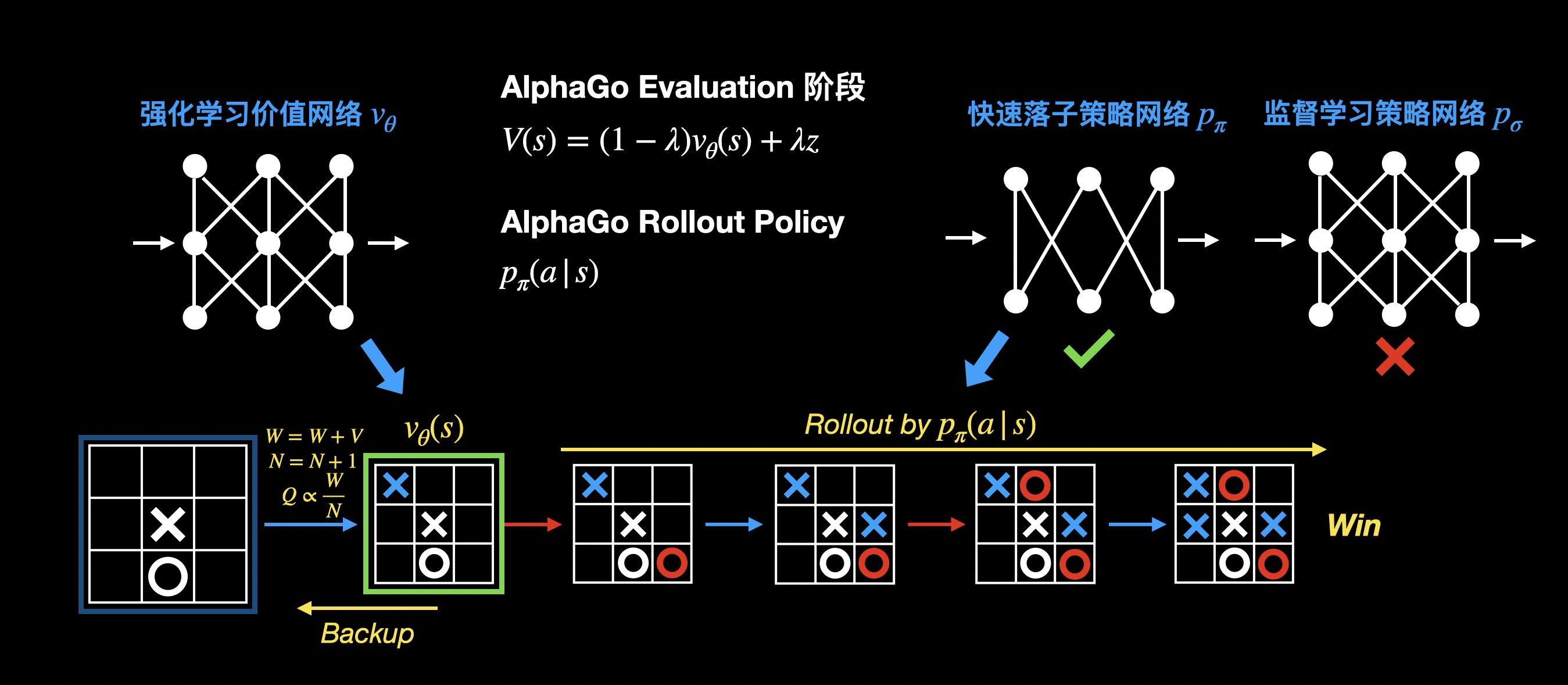
评估叶节点的价值时,结合了价值网络和 rollout 的结果。这里用的快速落子策略,是因为快速落子策略网络每步走棋速度更快,在等待价值网络评估结果前,可以进行更多次 rollout。
思考
可以看到 AlphaGo 的四个网络,在训练过程结束后就确定了。实际比赛中是采用固定的策略/价值网络模型结合蒙特卡洛树多次模拟的结果进行落子。蒙特卡洛树搜索依赖于策略和价值网络的指导,通过蒙特卡洛树搜索得到的落子策略,则强于策略网络给出的落子策略。同样的,蒙特卡洛树搜索多次 模拟得到的对棋局状态评估的准确度也比价值网络的评估更高。
如果可以用蒙特卡洛树搜索的结果,来优化策略和价值网络。然后基于优化后的策略价值网络,再次进行蒙特卡洛树搜索,以此不断循环,是不是可以得到一个更强的 AlphaGo 呢?
AlphaGo Zero
实际上,AlphaGo Zero 就是通过这种方式进行训练的:
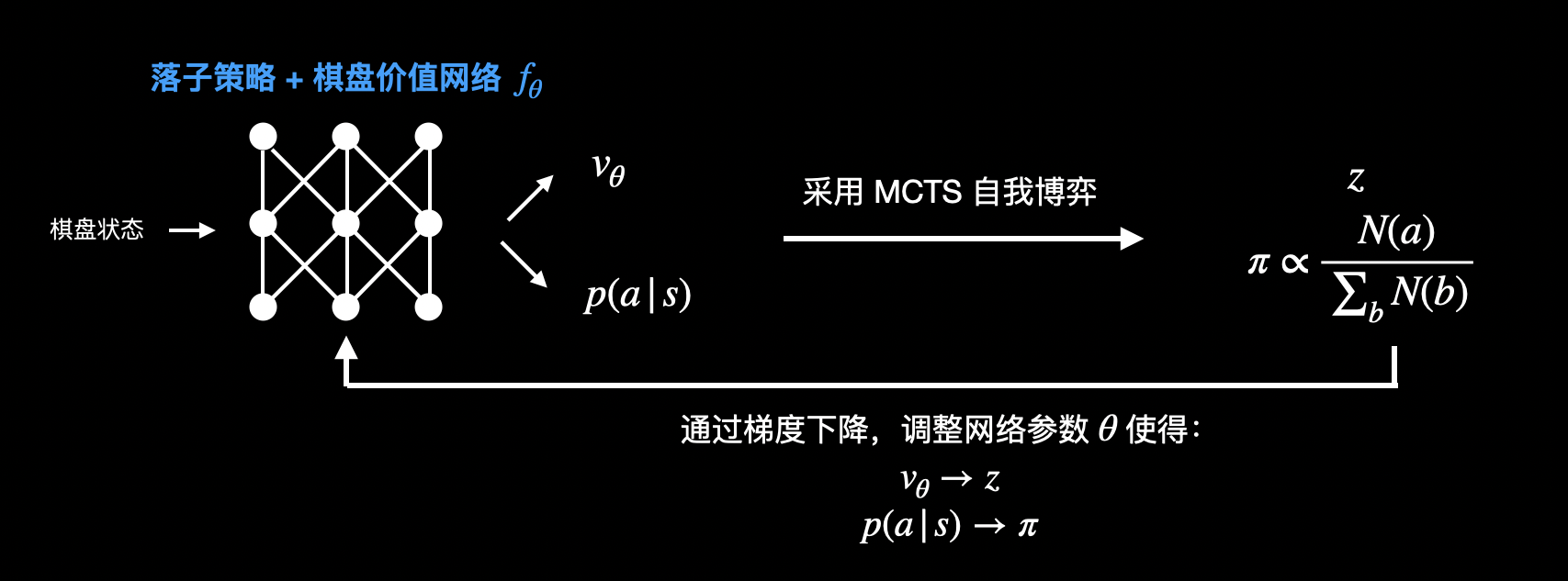
AlphaGo Zero 中只有一个网络,其同时输出落子策略和棋盘价值。并且 AlphaGo Zero 的蒙特卡洛树搜索,不会进行 rollout,直接采用价值网络输出来评估叶子节点的价值。因为 AlphaGo Zero 不需要人类的经验,自然没有人类经验可以作为 rollout 参考。另外 AlphaGo Zero 会不断根据蒙特卡洛树搜索去优化价值网络,所以可以直接使用价值网络来进行评估。
来看看 AlphaGo Zero 版本蒙特卡洛树搜索算法。
选择
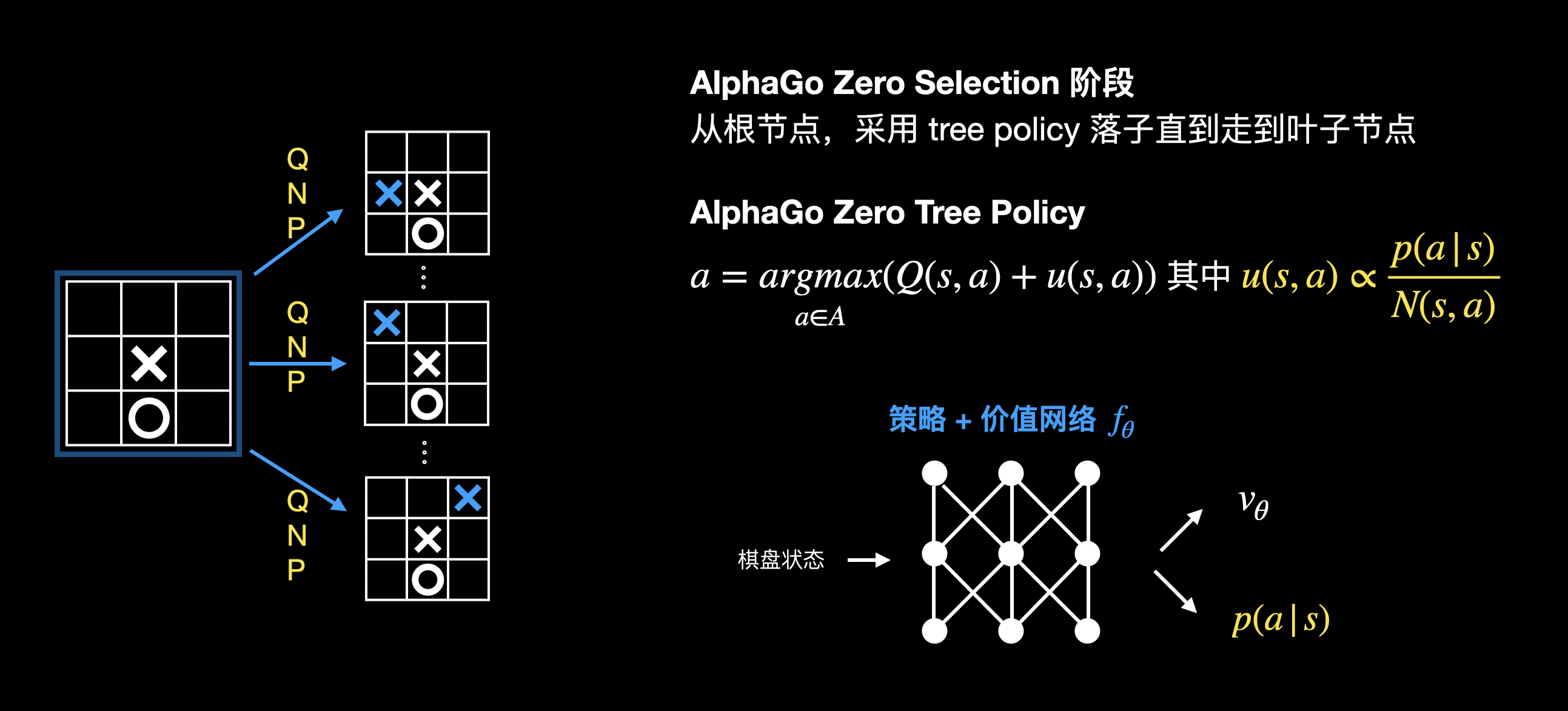
评估 & 回溯
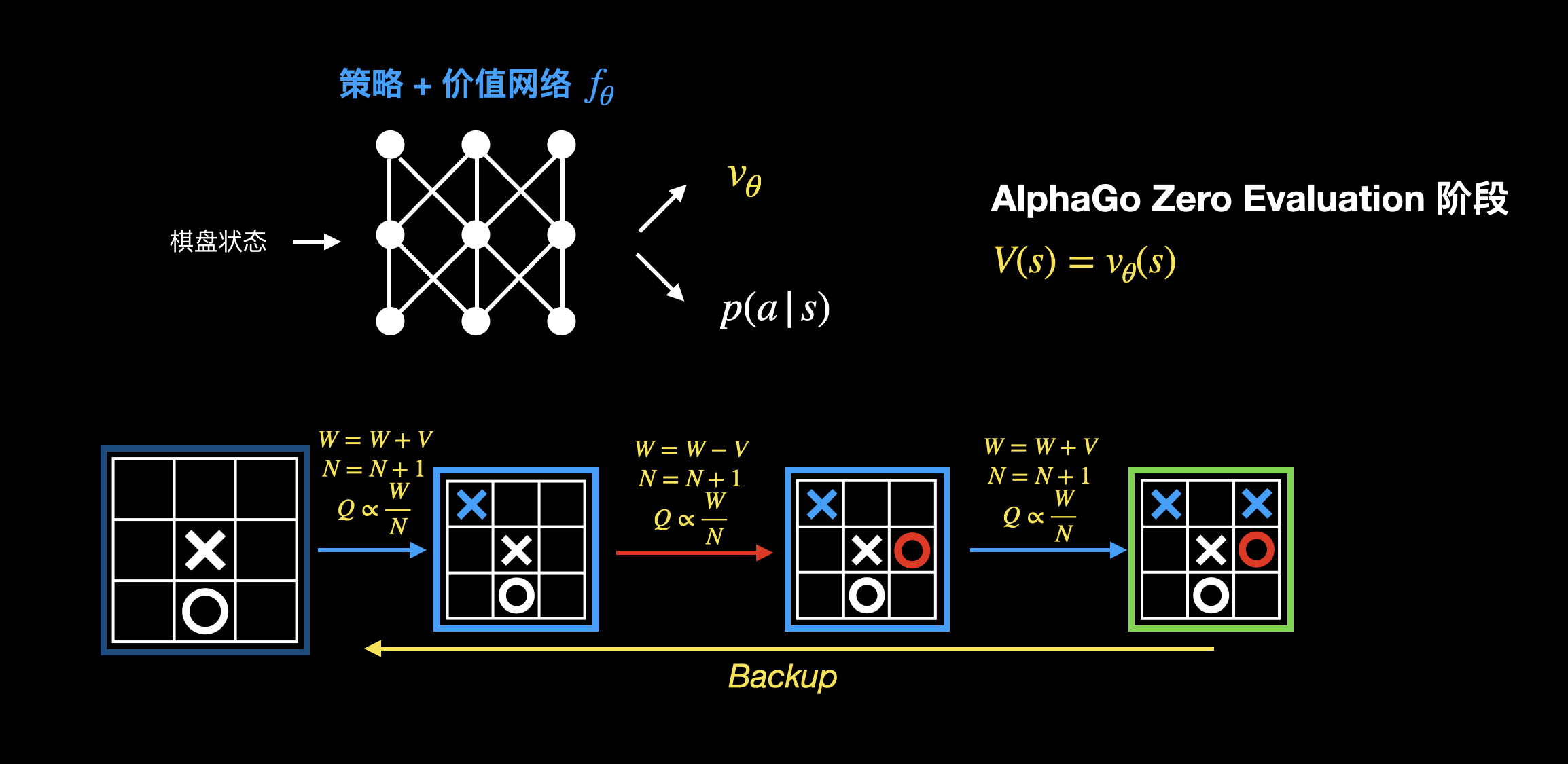
强化学习
至此,我们已经了解了 AlphaGo、AlphaGo Zero 是如何学习围棋。结合这些例子,我们来理解强化学习里的基本概念。
定义
强化学习属于机器学习的一种,通过试错的方式,训练代理以完成任务。
从这个定义我们可以看出,强化学习的关键在于试错。下图是强化学习的标准流程,代理在某个状态下,通过采取一个行动,得到相应的奖励,感知环境的变化从而进入下一个状态:
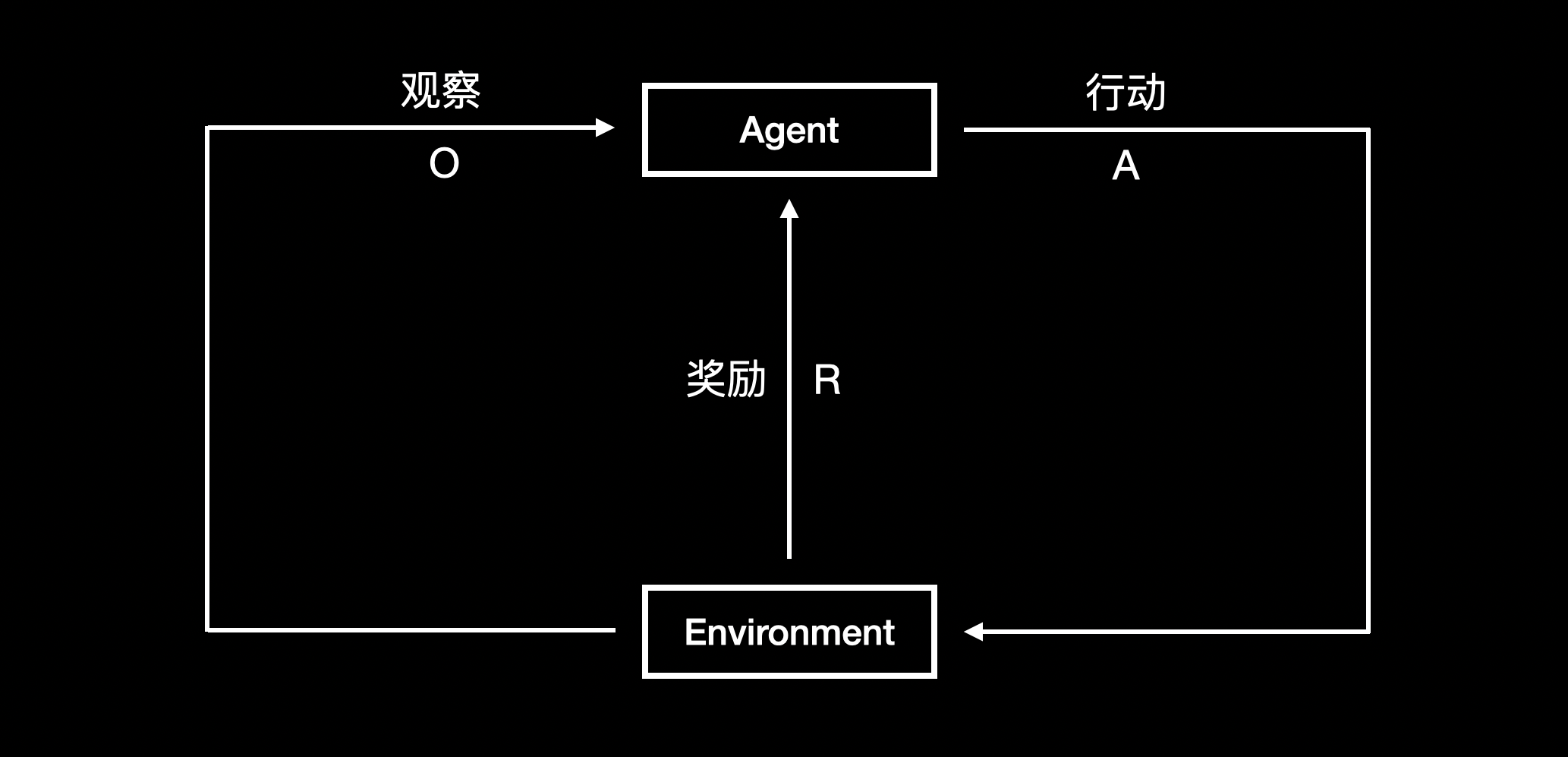
- 代理:即训练的对象,例如 AlphaGo。代理的目标是找到最佳行动策略以获得最大化预期回报
- 奖励:行动的好坏。强化学习中,反馈通常是延迟的。比如下棋,在终局之前每步落子的奖励都是 0,直到终局才有奖励
- 环境:接收代理的行动,返回对应的奖励和下一个状态
Model-Free vs Model-Based
有些强化学习会对环境进行建模,模拟环境输出奖励和下一个状态。根据是否对环境进行建模,强化学习分为 Model-Free 和 Model-Based 两个类别:
- Model-Free RL:不需要建模,从真实采样经验中直接学习价值函数/策略。但有些场景下真实数据获取成本高(例如无人机)
- Model-Based RL:从真实采样经验中先学习出环境的模型,用学到的模型规划行动。优点在于采样成本小,数据利用率高。缺点则是建模和真实的环境可能存在较大的偏差
下图是 Model-Based RL 的基础流程:
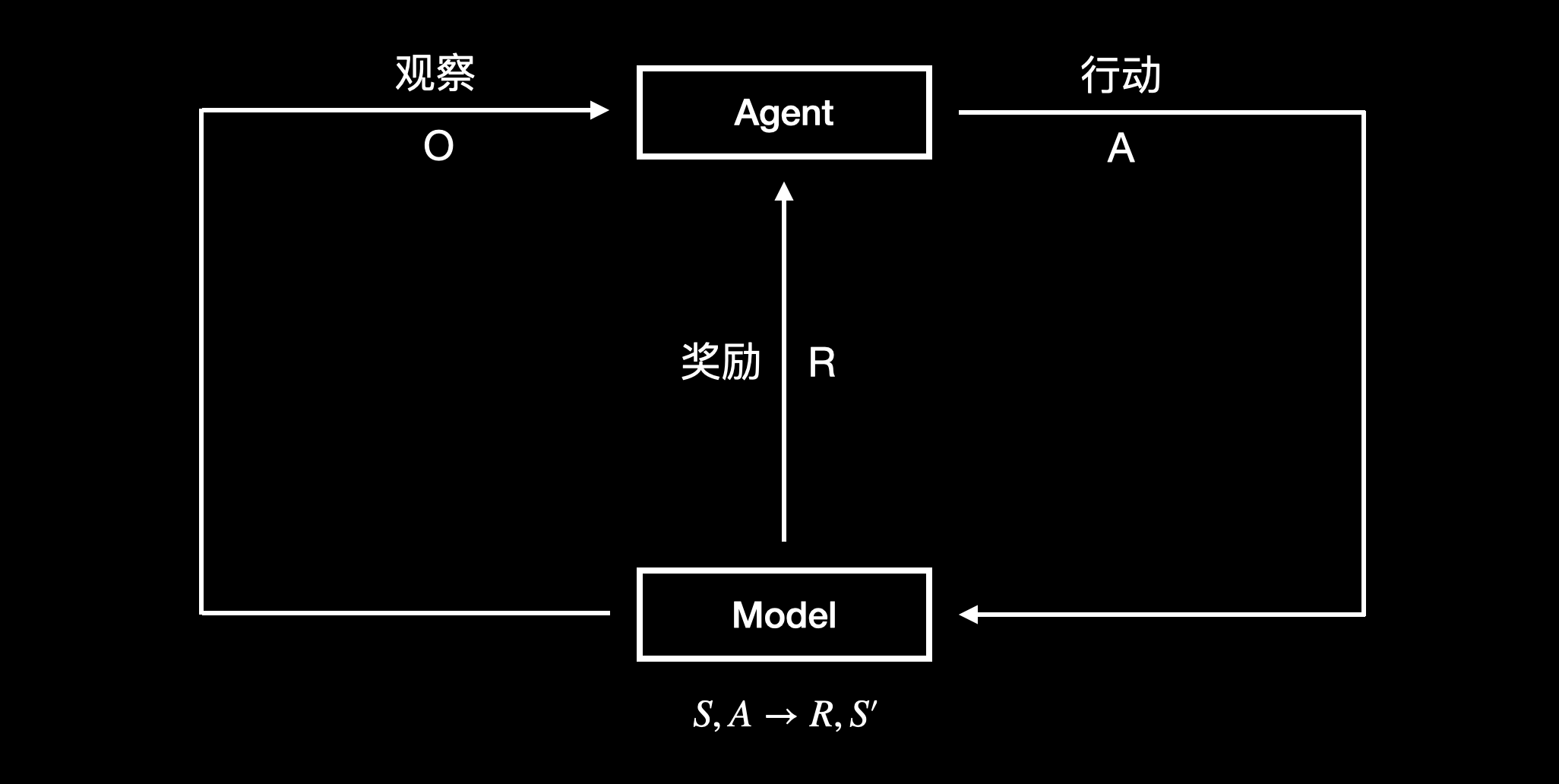
AlphaGo/AlphaGo Zero 属于 Model-Based RL。AlphaGo/AlphaGo Zero 在真正采取行动之前,会先在环境模型中进行无数遍模拟,这个步骤称为规划(planning),即代理在已知的环境模型中学习如何行动以获取最大收益。
Value-Based vs Policy-Based
强化学习的目标是找到最佳行动策略以达到最大收益。根据策略更新方式的不同,通常有两种类别:Value-Based 和 Policy-Based:
- Value-Based
- 直接学习价值函数,间接得到策略
- 收敛性差
- 只适用于离散动作空间
- Policy-Based
- 直接学习策略
- 收敛性好,但容易收敛到局部最优
- 适用于连续动作空间
- Actor Critic
- Value-Based 和 Policy-Based 的结合