线性回归
回归(regression)是能为一个或多个自变量与因变量之间关系建模的一类方法。 在机器学习领域中的大多数任务通常都与预测(prediction)有关。 当我们想预测一个或多个连续数值时,就会涉及到回归问题(如果是有限数量的离散数值,则属于分类问题)。
在机器学习领域,通常使用的是高维数据集。当我们的输入包含 $ d $ 个特征时,将所有特征放到向量 $\mathbf{x} \in \mathbb{R}^d$ 中, 并将所有权重放到向量 $\mathbf{w} \in \mathbb{R}^d$ 中,用 $\hat{y}$ 表示预测结果,可得:
\[\hat{y} = \mathbf{w}^\top \mathbf{x} + b\]上式中向量 $x$ 对应于单个数据样本的特征。 可以用矩阵 $\mathbf{X} \in \mathbb{R}^{n \times d}$ 表示 $n$ 个样本的数据集。 其中,$\mathbf{X}$ 的每一行是一个样本,每一列是一种特征。
对于特征集合 $\mathbf{X}$,预测值 $\hat{\mathbf{y}} \in \mathbb{R}^n$ 可以通过矩阵-向量乘法表示为:
\[{\hat{\mathbf{y}}} = \mathbf{X} \mathbf{w} + b\]给定训练数据特征 $\mathbf{X}$ 和对应的已知标签 $\mathbf{y}$, 线性回归的目标是找到一组权重向量 $\mathbf{w}$ 和偏置 $b$。当给定从 $\mathbf{X}$ 的同分布中取样的新样本特征时, 这组权重向量和偏置能够使得新样本预测标签的误差尽可能小。
损失函数
在开始考虑如何用模型拟合数据之前,需要知道如何度量模型的拟合程度。损失函数能够量化目标的实际值与预测值之间的差距。 通常我们会选择非负数作为损失,且数值越小表示损失越小,完美预测时的损失为0。 回归问题中最常用的损失函数是均方误差函数。
均绝对误差函数 Mean Absolute Error Function
Mean Absolute Error Function (MAE) 通常也称为 L1 损失函数。当样本 $i$ 的预测值为 $\hat{y}^{(i)}$,其相应的真实标签为 $y^{(i)}$ 时, 均绝对误差可以定义为以下公式:
\[L(\mathbf{w}, b) =\frac{1}{n}\sum_{i=1}^n l^{(i)}(\mathbf{w}, b) =\frac{ \sum_{i=1}^n|\hat{y}^{(i)}-y^{(i)}|}{n}\]均方误差函数 Mean Square Error Function
Mean Square Error Function (MSE) 通常也称为 L2 损失函数。当样本 $i$ 的预测值为 $\hat{y}^{(i)}$,其相应的真实标签为 $y^{(i)}$ 时, 平方误差可以定义为以下公式:
\[l^{(i)}(\mathbf{w}, b) = \frac{1}{2} \left(\hat{y}^{(i)} - y^{(i)}\right)^2\]为了度量模型在整个数据集上的质量,我们需计算在训练集 $n$ 个样本上的损失均值:
\[L(\mathbf{w}, b) =\frac{1}{n}\sum_{i=1}^n l^{(i)}(\mathbf{w}, b) =\frac{1}{n} \sum_{i=1}^n \frac{1}{2}\left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)^2\]Huber Loss
在 MSE 的计算中,异常点会因为平方而进一步放大,导致了异常点会对训练过程造成很大的影响。而 MAE 是取绝对值,异常点的影响不会被放大。MAE 的最优解是中位数形式的,MSE 的最优解是均值形式的,显然中位数对于异常点的影响会更小。
但 MAE 也存在一个问题,特别是对于神经网络来说,它的梯度在极值点处会有很大的跃变。为了解决这个问题,需要在解决极值点的过程中动态减小学习率。MSE 在极值点却有着良好的特性,即使是固定学习率下也能收敛。MSE 的梯度随着损失函数的减小而减小,这一特性使得它在最后的训练过程中能得到更精确的结果。
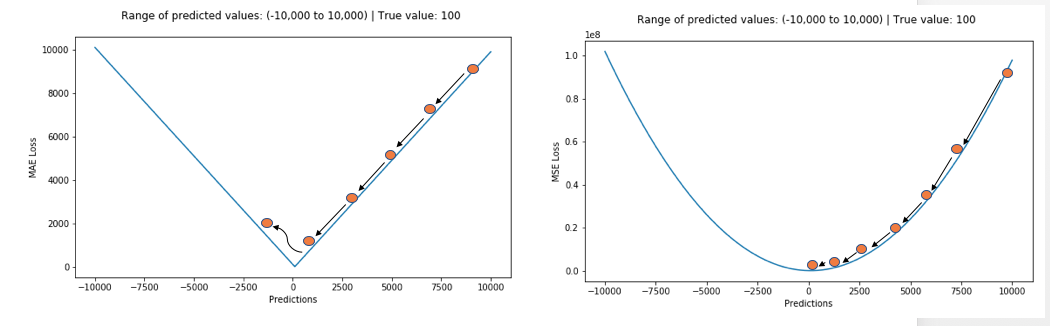
为了权衡二者的利弊,Huber 在1964年提出了 Huber loss,其形式如下:
\[L_{\delta}= \left\{\begin{matrix} \frac{1}{2}(y - \hat{y})^{2} & if \left | (y - \hat{y}) \right | < \delta\\ \delta ((y - \hat{y}) - \frac1 2 \delta) & otherwise \end{matrix}\right.\]当误差的绝对值小于 $ \delta $ 时采用 MSE,大于 $ \delta $ 时采用 MAE,而且该函数是连续且可微的。
思考:
- 如何证明是连续可微的?
- 为什么要求是连续可微的?
交叉熵损失函数 Cross Entropy Loss
在二分类的情况下,模型最后需要预测的结果只有两种情况,对于每个类别我们的预测得到的概率为 $p$ 和 $1-p$ ,样本 $i$ 的真实 label 为 $y_i$ 。此时表达式为:
\[L=\frac{1}{n}\sum\limits_il^{(i)}=\frac{1}{n}\sum\limits_i-{[y_i\log(p_i) + (1 - y_i)\log(1 - p_i)]}\]多分类的情况实际上就是对二分类的扩展:
\[L=\frac{1}{n}\sum\limits_il^{(i)}=-\frac{1}{n}\sum\limits_i\sum_{c=1}^My_{i,c}\log(p_{i,c})\]其中:
- $M$ 表示 label 的数量,即总类别数
- $y_{i,c}$ 表示如果样本 $i$ 的真实 label 为 $c$ 则取 $1$,否则取 $0$
- $p_{i,c}$ 表示观察样本 $i$ 的 label 为 $c$ 的预测概率
样例
| 预测 | 真实 | 正确性 |
|---|---|---|
| 0.3 0.3 0.4 | 0 0 1 (猪) | 正确 |
| 0.3 0.4 0.3 | 0 1 0 (狗) | 正确 |
| 0.1 0.2 0.7 | 1 0 0 (猫) | 错误 |
由:
\[l^{(1)}=-(0 \times log0.3 + 0 \times log0.3 + 1 \times log0.4) = 0.91\] \[l^{(2)}=-(0 \times log0.3 + 1 \times log0.4 + 0 \times log0.3) = 0.91\] \[l^{(3)}=-(1 \times log0.1 + 0 \times log0.2 + 1 \times log0.7) = 2.30\]可得:
\[L = \frac{0.91+0.91+2.30}{3} = 1.37\]损失函数数学推导
损失函数对比
- MSE 适用于回归问题,不适用于分类问题
- MSE 预测值和目标值的欧式距离。分类问题中 label 值的大小在欧氏空间中是没有意义的。所以分类问题不适合用 mse 作为损失函数。
- 分类问题属于逻辑回归,必须有激活函数这个非线性单元在,通常是 sigmoid(也可以是其他非线性激活函数) 逻辑回归为什么用Sigmoid。MSE + sigmoid 会有梯度消失的问题(见下一篇文章《线性回归到深度网络》),导致学习速率慢。另一方面,MSE 的导数是非凸函数,有多个极值点,求解最优解困难。
- 交叉熵适用于分类问题,不适用于回归问题
- 交叉熵是信息论的概念。交叉熵能够衡量同一个随机变量中的两个不同概率分布的差异程度,在机器学习中就表示为真实概率分布与预测概率分布之间的差异。交叉熵的值越小,模型预测效果就越好。
- 交叉熵损失函数只和分类正确的预测结果有关系,而 MSE 的损失函数还和错误的分类有关系,该分类函数除了让正确的分类尽量变大,还会让错误的分类变得平均,在分类问题中这个调整是没有必要的。但是对于回归问题来说,这样的考虑就显得很重要了。所以,回归问题熵使用交叉上并不合适。
- 思考:交叉熵是否也存在梯度消失的问题?
梯度下降 Gradient Descent
前面提到,损失函数是量化目标的实际值与预测值间的差距,损失函数越小意味着我们的预测越贴近真实值,因此我们的目标是最小化损失函数。而最常见的方法,就是梯度下降。
感官认识
把损失函数的值想象成一座山,寻找损失函数的最小值,可以理解寻找山的最低点。我们只需要沿着向下的斜坡一直走,就可以找到局部最低点:
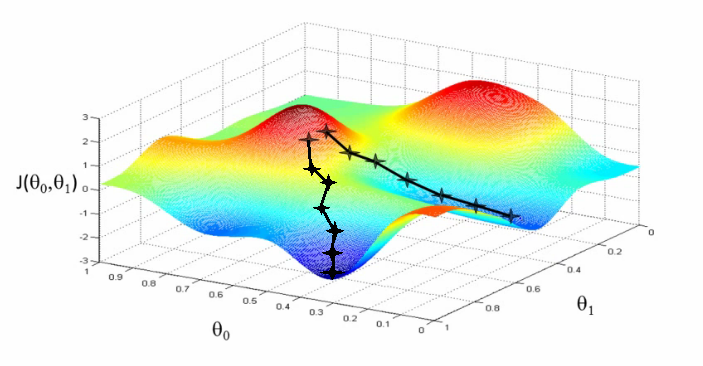
梯度下降就是这样一个思路,梯度可以理解为坡度,梯度下降可以理解为朝着下坡的方向前进。
梯度的定义
导数、偏导数以及方向导数
一元函数的情况下,导数就是函数的变化率,从几何意义上看,切点处的导数值就是切线的斜率。
偏导数是多元函数“退化”成一元函数时的导数,这里“退化”的意思是固定其他自变量的值,只保留一个自变量,则 $N$ 元函数有 $N$ 个偏导数。一个自变量对应一个坐标轴,偏导数为函数在每个位置处沿着自变量坐标轴方向上的导数(切线斜率)。
如果是方向不是沿着坐标轴方向,而是任意方向,则为方向导数。方向导数是函数在任意方向上的导数。具体地,定义 $xy$ 平面上一点 $(a,b)$ 以及单位向量 $\vec{u}=(cos\theta, sin\theta)$,在曲面 $z=f(x,y)$ 上,从点 $(a,b,f(a,b))$ 出发,沿 $\vec{u}=(cos\theta, sin\theta)$ 方向走 $t$ 单位长度后,函数值 $z$ 为$F(t)=f(a+tcosθ,b+tsinθ)$,则点 $(a,b)$ 处 $\vec{u}=(cos\theta, sin\theta)$ 方向的方向导数为:
\[\begin{align} & \quad \frac{d}{dt}f(a+tcos\theta, b+tsin\theta)\\ &= \mathop{lim}\limits_{t\rightarrow0}\frac{f(a+tcos\theta, b+tsin\theta)-f(a,b)}{t} \\ &=\mathop{lim}\limits_{t\rightarrow0}\frac{f(a+tcos\theta, b+tsin\theta)-f(a,b+tsin\theta)}{t}+\mathop{lim}\limits_{t\rightarrow0}\frac{f(a, b+tsin\theta)-f(a,b)}{t} \\ &= \frac{\partial}{\partial x}f(a,b)\frac{dx}{dt} + \frac{\partial}{\partial y}f(a,b)\frac{dy}{dt} \\ &= f_x(a, b)cos\theta + f_y(a,b)sin\theta \\ &= (f_x(a,b), f_y(a,b))\cdot(cos\theta, sin\theta) \end{align}\]其中,$f_x(a,b)$ 和 $f_y(a,b)$ 分别为函数在 $(a,b)$ 位置的偏导数。由上面的推导可知,方向导数是偏导数的线性组合,系数为该方向的单位向量。当该方向与坐标轴正方向一致时,方向导数即偏导数,换句话说,偏导数为坐标轴方向上的方向导数。
梯度
梯度,通常用数学符号 $\nabla$ 表示。 二元时为 $(\frac{∂z}{∂x},\frac{∂z}{∂y})$,多元时为 $(\frac{∂z}{∂x},\frac{∂z}{∂y},…)$。
继续上面方向导数的推导,$(a,b)$ 处 $\theta$ 方向上的方向导数为
\[\begin{align} & \quad (f_x(a,b), f_y(a,b))\cdot(cos\theta, sin\theta)\\ &=|(f_x(a,b), f_y(a,b))|\cdot|1|\cdot cos\phi \\ &= |\nabla f(a,b)|\cdot cos\phi \end{align}\]其中 $ \phi $ 为 $ \nabla f(a,b) $ 与 $ \vec{u} $ 的夹角。当 $ \phi = 0 $ 即 $ \vec{u} $ 与梯度 $ \nabla f(a,b) $ 同向时,方向导数取最大值,最大值为 $ |\nabla f(a,b)| $。当 $ \phi = \pi $ 即 $ \vec{u} $ 与梯度 $ \nabla f(a,b) $ 反向时,方向导数取最小值,为 $ -|\nabla f(a,b)|$。
至此引入梯度的几何意义:
- 给定位置的梯度方向,为函数在该位置处方向导数最大的方向,也是函数值上升最快的方向,反方向为下降最快的方向
- 当前位置的梯度长度(模),为最大方向导数的值
总结
- 偏导数构成的向量为梯度
- 方向导数为梯度在该方向上的线性合成,系数为该方向的单位向量
- 梯度方向为方向导数最大的方向,梯度的模为最大的方向导数
梯度下降
前面提到梯度方向即函数值上升最快的方向,如果我们要寻找损失函数的最小值,那只需要朝着损失函数的梯度的反方向前进即可。定义损失函数 $L(\mathbf{w}, b)$,其梯度为:
\[\nabla L(\mathbf{w},b) = (\frac{\partial L(\mathbf{w},b)}{\partial \mathbf{w}}, \frac{\partial L(\mathbf{w},b)}{\partial b})\]想找到损失函数的局部最小值,需要沿着梯度的反方向更新参数值,直到收敛:
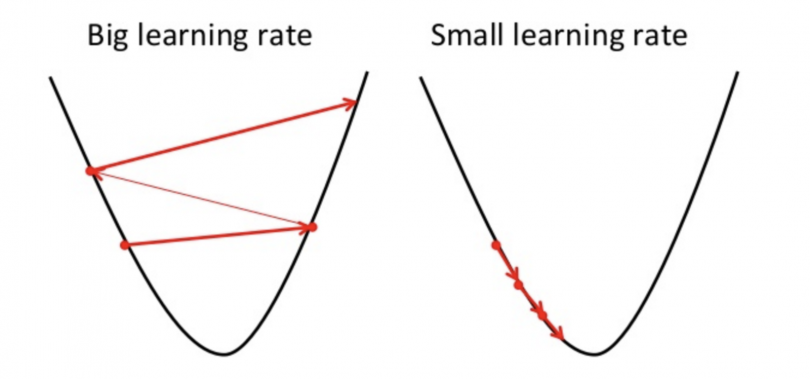
\[\begin{align} repeat \ \ until \ \ convergence \ \ \{ \\ & \mathbf{w} \leftarrow \mathbf{w} - \alpha\frac{\partial L(\mathbf{w},b)}{\partial \mathbf{w}} \\ & b \leftarrow b - \alpha\frac{\partial L(\mathbf{w},b)}{\partial b} \\ \} \end{align}\]其中 $\alpha$ 表示更新步长,也称为学习率。步长如果太小,则迭代速度太慢,步长如果过大,则可能出现不收敛,如下图:
梯度下降算法
批量梯度下降法 Batch Gradient Descent
Batch Gradient Descent(BGD)使用全部的样本进行梯度计算并更新参数。
- 优点:稳定,可收敛。
- 缺点:计算量大耗时大,内存占用大,稳定意味着容易陷入局部最优。
随机梯度下降法 Stochastic Gradient Descent
Stochastic Gradient Descent(SGD)区别在与每次随机选取一个样本计算梯度并更新参数。
- 优点:快,不容易陷入局部最优。
- 缺点:噪音较 BGD 要多,使得 SGD 并不是每次迭代都向着整体最优化方向。
小批量梯度下降法 Mini-batch Gradient Descent
Mini-batch Gradient Descent(MBGD)是批量梯度下降法和随机梯度下降法的折衷,每次随机选一批样本计算梯度并更新参数。MBGD 是最常在实践中使用的梯度下降算法。
梯度下降法和其他无约束优化算法的比较
在机器学习中的无约束优化算法,除了梯度下降以外,还有最小二乘法,此外还有牛顿法和拟牛顿法。
梯度下降法和最小二乘法相比,梯度下降法需要选择步长,而最小二乘法不需要。梯度下降法是迭代求解,最小二乘法是计算解析解。如果样本量不算很大,且存在解析解,最小二乘法比起梯度下降法要有优势,计算速度很快。但是如果样本量很大,用最小二乘法由于需要求一个超级大的逆矩阵,这时就很难或者很慢才能求解解析解了,使用迭代的梯度下降法比较有优势。
梯度下降法和牛顿法/拟牛顿法相比,两者都是迭代求解,不过梯度下降法是梯度求解,而牛顿法/拟牛顿法是用二阶的海森矩阵的逆矩阵或伪逆矩阵求解。相对而言,使用牛顿法/拟牛顿法收敛更快。但是每次迭代的时间比梯度下降法长。