概率 Probability vs. 推断 Inference
在概率论中,通常我们会告知某个事件发生的概率是多少。比如一枚硬币正面朝上的概率是 0.5,在这个前提下,再继续计算复杂事件发生的概率,例如:投 10 次硬币,出现正面朝上的概率是多大?
\[\binom{10}{4}\times(0.5^4)\times(0.5^{10-4}) = 0.205\]而在统计学中,相反,我们不知道某事件发生的概率,而是通过观察得到数据,比如观察投 10 次硬币,观察到有 4 次硬币朝上。通过观察的数据来计算出符合观察结果的“最佳”概率估计。似然法 (likelihood) 就是我們进行概率估算的最佳手段。
似然函数和极大似然
在概率论和统计学中,二项分布是 $n$ 个独立的成功/失败试验中成功的次数的离散概率分布,其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验。一般如果随机变量 $X$ 服从参数为 $n$ 和 $p$ 的二项分布,我们记为 $X\sim B(n,p)$。$n$ 次试验中正好得到 $k$ 次成功的概率由概率质量函数给出:
\[P(X=k)=\binom{n}{k}p^k(1-p)^{n-k}\]以上述抛硬币为例,我們假定硬币朝上与否是一个服从二项分布的随机变量,$X\sim B(10,\pi)$。我们观察到,10 次实验中有 4 次硬币朝上,即 $k=4$:
\[P(X=4)=\binom{10}{4}p^4(1-p)^{10-4}\]此时硬币朝上的概率 $p$ 未知,而我们想要知道,$p$ 取多少时,$P(X=4)$ 的值会最大?即单次抛硬币朝上的概率 $p$ 为多少时,10 次实验中出现 4 次硬币朝上的概率最大?
因此问题可以转化为,定义一个关于概率 $p$ 的函数:
\[L(p|X=4)=\binom{10}{4}p^4(1-p)^{10-4}\]找到对应的 $p$ 值使得该函数的值最大,这个函数也称为似然函数。
对数似然函数
似然函数的最大值,也可以通过求似然函数的对数函数的最大值获得。
证明:当方程 $L(p)$ 的對數方程 $\text{log}L(p)$ 是最大值时,$L(p)$ 也是最大值。
如果 $L(p)$ 是连续可导,只有一个最大值,且可以二次求导。则当 $L(p)$ 取最大值时满足:
\[\frac{dL}{d\theta}=0, \ \frac{d^2L}{d\theta^2}<0\]令 $\ell=\text{log}L$,由 $\frac{d\ell}{dL}=\ell^\prime=\frac{1}{L}$ 可得:
\[\frac{d\ell}{d\theta}=\frac{d\ell}{dL}\cdot\frac{dL}{d\theta}=\frac{1}{L}\cdot\frac{dL}{d\theta}\]当 $\ell(p)$ 取最大值时:
\[\begin{align} \frac{d\ell}{d\theta} & =0\Leftrightarrow\frac{1}{L}\cdot\frac{dL}{d\theta}=0\\ & \because \frac{1}{L}\neq0 \\ & \therefore \frac{dL}{d\theta}=0 \end{align}\] \[\begin{align} \frac{d^2\ell}{d\theta^2} &= \frac{d}{d\theta}(\frac{d\ell}{dL}\cdot\frac{dL}{d\theta})\\ &= \frac{d\ell}{dL}\cdot\frac{d^2L}{d\theta^2} + \frac{dL}{d\theta}\cdot\frac{d}{d\theta}(\frac{d\ell}{dL}) \end{align}\]$\frac{d^2\ell}{d\theta^2}<0$ 且 $\frac{dL}{d\theta}=0$,因为 $L$ 表示概率 $L \ge 0$,所以 $\frac{d\ell}{dL} = \frac{1}{L} \ge 0$,可得 $\frac{d^2L}{d\theta^2}<0$ 。
因此如果 $\ell(p)$ 取最大值,可以推导出 $\frac{dL}{d\theta}=0$ 且 $\frac{d^2L}{d\theta^2}<0$ ,因此 $L(p)$ 也为最大值。
对数的好处是在于可以把乘除转化为加减。当有多个独立的观察时,总似然函数等于各个观察值的似然函数的乘积:
\[L(\theta|x_1,\cdots,x_n)=f(x_1,\cdots,x_n|\theta)=\prod_{i=1}^nf(x_i|\theta)\]如果用对数似然函数表示,则变成各个观察值的对数似然函数的和:
\[\ell(\theta|x_1,\cdots,x_n)=\sum_{i=1}^n\text{log}(f(x_i|\theta))\]极大似然和损失函数
最大似然函数可以推导出不同的损失函数。分类问题中(包括二分类和多分类),可推导出交叉熵损失函数;在回归问题中,可以推导出均方差损失。
均方差损失
假定我们有一个观测的数据集 $\mathbf{x} = (x_1, . . . , x_N )^T$ ,表示标量变量 $x$ 的 $N$ 次观测。我们假定各次观测是独立地从高斯分布中抽取的,分布的均值 $\mu$ 和方差 $\sigma^2$ 未知,希望根据数据集来确定这些参数。由于我们的数据集 $\mathbf{x}$ 是独立同分布的,因此给定 $\mu$ 和 $\sigma^2$,我们可以给出数据集的概率:
\[p(\mathbf{x}|\mu,\sigma^2)= \prod\limits_{n=1}^{N}\mathcal N(x_n|\mu, \sigma^2)\]当把上式看成 $\mu$ 和 $\sigma$ 的函数时,其就是高斯分布的似然函数。如下图:
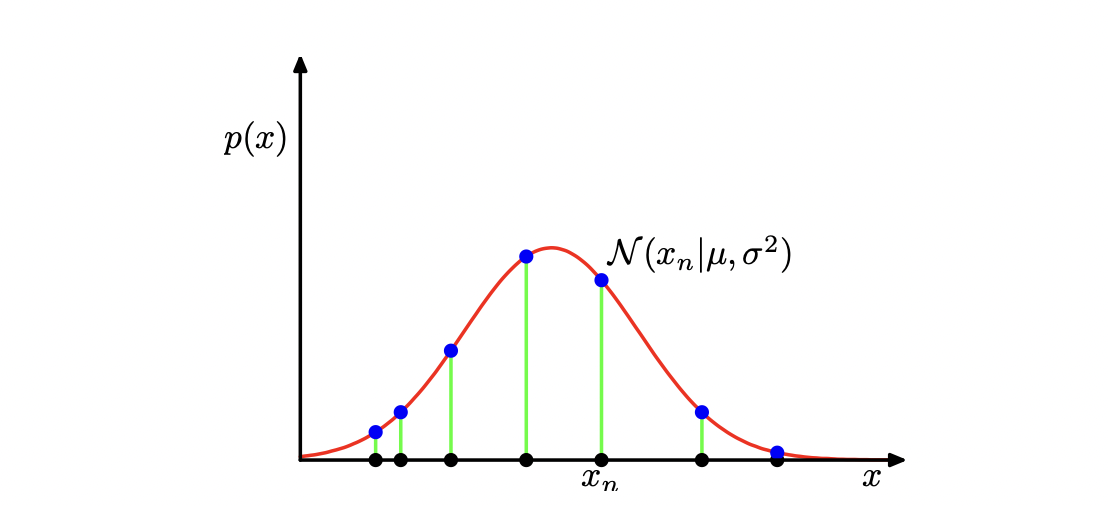
高斯概率分布的似然函数,由红色曲线表示。这里,黑点表示数据集 ${x_n}$的值,似然函数对应于蓝色值的乘积。最大化似然函数涉及到调节高斯分布的均值和方差,使得这个乘积最大。
前面提到,最大化某个函数的对数等价于最大化这个函数。
\[\ln p(\mathbf{x}|\mu, \sigma^2)=-\frac{1}{2\sigma^2}\sum\limits_{n=1}^N(x_n-\mu)^2 - \frac{N}{2}\ln \sigma^2-\frac{N}{2}\ln(2\pi)\]关于$\mu$,最大化该函数,可得最大似然解:
\[\mu_{ML}=\frac{1}{N}\sum\limits_{n=1}^Nx_n\]关于 $\sigma^2$,最大化该函数:
\[\sigma^2 = \mathop{\operatorname{arg\,max}}\limits_\sigma \sum\limits_{n=1}^N(-\frac{\ln\sigma^2}{2}-\frac{1}{2\sigma^2}(x_n-\mu)^2)\]单调递增,导数为 0 时为最大值,用 $\delta$ 表示 $\sigma^2$, 即:
\[\frac{\partial}{\partial\delta}\sum\limits_{n=1}^N(-\frac{\ln\delta}{2}-\frac{1}{2\delta}(x_n-\mu)^2)=0\] \[\sum\limits_{n=1}^N(-\frac{1}{2\delta}+\frac{1}{2}(x_n - \mu)^2\delta^{-2}) = 0\] \[\sum\limits_{n=1}^N(-\frac{1}{\delta}+(x_n - \mu)^2\delta^{-2}) = 0\] \[\sum\limits_{n=1}^N(-\delta+(x_n - \mu)^2) = 0\]可得当 $\delta = \frac{1}{N}\sum\limits_{n=1}^N(x_n - \mu)^2$ 时导数为 0,似然方程为最大值,最大似然解:
\[\sigma^2 = \frac{1}{N}\sum\limits_{n=1}^N(x_n - \mu)^2\]注:在高斯分布的情况下,$\mu$ 的解和 $\sigma^2$ 无关,因此可以首先求解 $\mu$ 再求解 $\sigma^2$。
因此,最大化似然函数等价于最小化均方差损失。
交叉熵损失
K 分类问题下,单个样本服从的分布如下:
\[p(y|x;p)=\prod\limits_{k=1}^Kp_k^{y_k}\]则 N 个样本下的似然函数为:
\[L(p(X))=\prod\limits_{n=1}^N\prod\limits_{k=1}^Kp_k^{y_k}\]最大化似然函数,即最小化负对数似然函数:
\[min -\sum\limits_{n=1}^N \sum\limits_{k=1}^K y_k log p_k\]上式也即是多分类下常用的交叉熵损失函数。因为是多分类问题,一个样本只属于一个分类,即只有一个 $y_k$ 等于 1。故上述函数可简化为:
\[min -\sum\limits_{n=1}^N log P(y_k=1)\]