查询、键和值 Query & Key-Value
注意力机制中,给定一个查询(query)和一组键值对(key-value pairs)作为输入,通过 Compatibility Function 计算出查询和每个键的关联度,再用计算出的关联度作为权重系数乘以每个键对应的值,得到的加权值(weight sum)作为输出。
An attention function can be described as mapping a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors. The output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key.
注意力汇聚
查询和键之间的交互形成了注意力汇聚, 注意力汇聚有选择地聚合了值以生成最终的输出。
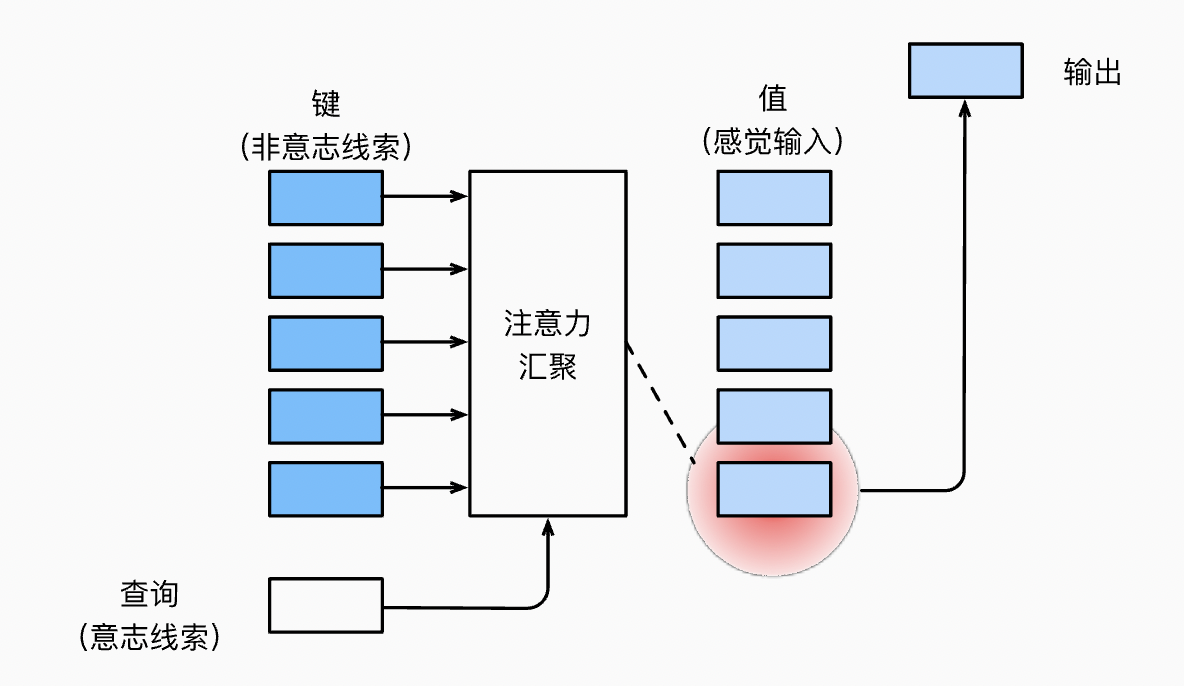
非参数注意力汇聚
所谓非参数注意力汇聚,就是指没有需要学习的参数。公式定义如下:
\[f(x) = \sum_{i=1}^n \frac{K(x - x_i)}{\sum_{j=1}^n K(x - x_j)} y_i\]其中 $K$ 是核。考虑用高斯核 $K(u) = \frac{1}{\sqrt{2\pi}} \exp(-\frac{u^2}{2})$ 作为核函数,代入可得:
\[\begin{aligned} f(x) &=\sum_{i=1}^n \alpha(x, x_i) y_i\\ &= \sum_{i=1}^n \frac{\exp\left(-\frac{1}{2}(x - x_i)^2\right)}{\sum_{j=1}^n \exp\left(-\frac{1}{2}(x - x_j)^2\right)} y_i \\&= \sum_{i=1}^n \mathrm{softmax}\left(-\frac{1}{2}(x - x_i)^2\right) y_i. \end{aligned}\]从上式可以看出,如果一个键 $x_i$ 越接近给定的查询 $x$, 那么分配给这个键对应值 $y_i$ 的注意力权重就越大, 也就“获得了更多的注意力”。
带参数注意力汇聚
可以很简单扩展为带参数的注意力汇聚:
\[\begin{aligned}f(x) &= \sum_{i=1}^n \alpha(x, x_i) y_i \\&= \sum_{i=1}^n \frac{\exp\left(-\frac{1}{2}((x - x_i)w)^2\right)}{\sum_{j=1}^n \exp\left(-\frac{1}{2}((x - x_j)w)^2\right)} y_i \\&= \sum_{i=1}^n \mathrm{softmax}\left(-\frac{1}{2}((x - x_i)w)^2\right) y_i.\end{aligned}\]注意力评分函数
高斯核的指数部分可以视为注意力评分函数(attention scoring function), 简称评分函数(scoring function), 然后把这个函数的输出结果输入到 softmax 函数中进行运算,得到与键对应的值的概率分布(即注意力权重)。 最后,注意力汇聚的输出就是基于这些注意力权重的值的加权和。
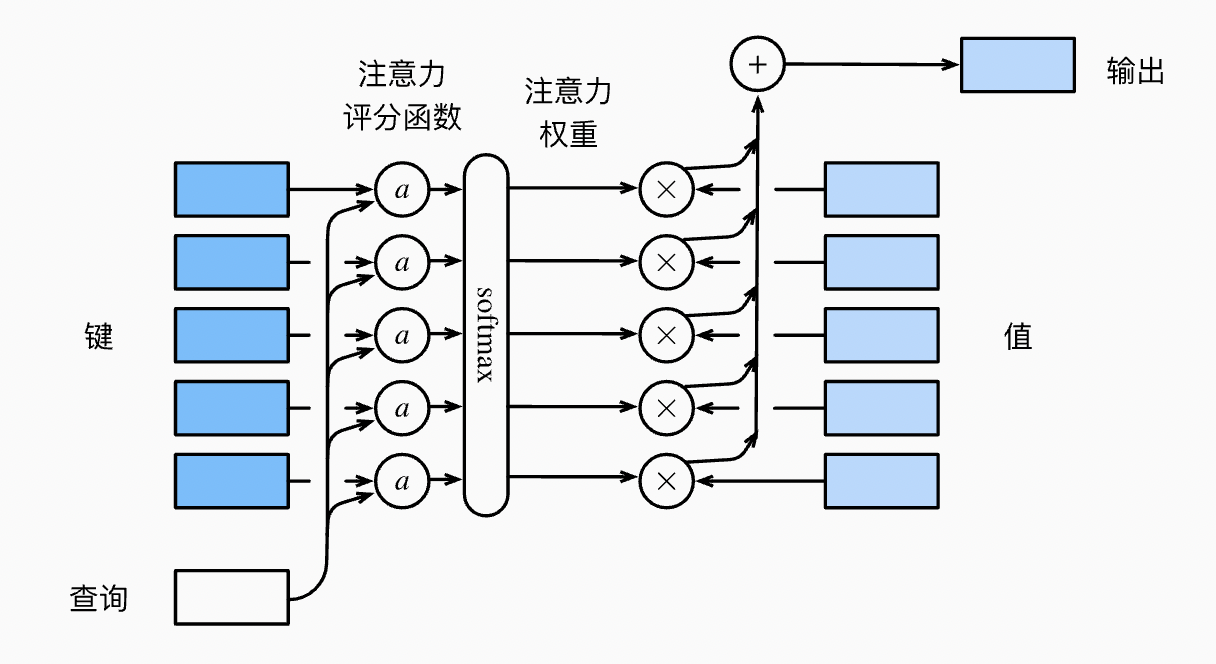
加性注意力
当查询和键是不同长度的矢量时, 可以使用加性注意力作为评分函数。 给定查询 $\mathbf{q} \in \mathbb{R}^q$ 和键 $\mathbf{k} \in \mathbb{R}^k$, 加性注意力(additive attention)的评分函数为:
\[a(\mathbf q, \mathbf k) = \mathbf w_v^\top \text{tanh}(\mathbf W_q\mathbf q + \mathbf W_k \mathbf k) \in \mathbb{R}\]其中可学习的参数是 $\mathbf W_q\in\mathbb R^{h\times q}$、$\mathbf W_k\in\mathbb R^{h\times k}$ 和 $\mathbf w_v\in\mathbb R^{h}$。其将查询和键连结起来后输入 MLP 中, MLP 包含一个隐藏层,其隐藏单元数是一个超参数 $h$。 通过使用 $tanh$ 作为激活函数。
缩放点积注意力
若查询和键具有相同的长度 $d$,则可以采用缩放点积注意力:
\[a(\mathbf q, \mathbf k) = \mathbf{q}^\top \mathbf{k} /\sqrt{d}\]在实践中,我们通常从小批量的角度来考虑提高效率, 例如基于 $n$ 个查询和 $m$ 个键值对计算注意力, 其中查询和键的长度为 $d$,值的长度为 $v$。 查询 $\mathbf Q\in\mathbb R^{n\times d}$、 键 $\mathbf K\in\mathbb R^{m\times d}$ 和 值 $\mathbf V\in\mathbb R^{m\times v}$ 的缩放点积注意力是:
\[\mathrm{softmax}\left(\frac{\mathbf Q \mathbf K^\top }{\sqrt{d}}\right) \mathbf V \in \mathbb{R}^{n\times v}\]