对虚数、复数的理解,分享两篇不错的文章:
本文是摘抄这两篇文章的笔记。
虚数
Visual Understanding of Negative and Complex Numbers
表达式 $x^2 = 9$ 可以拆解为 $1 \cdot x \cdot x = 9$。可以将 $x$ 的求解转换为: 求解变换 $x$,当其应用两次时,1 变为 9。
答案分别是 “$x = 3$” 和 “$x = -3$”,即可以通过”缩放3倍”或”缩放3倍并翻转”来实现这个变换。
考虑 $i^2 = -1$,同样拆解为 $1 \cdot i \cdot i = -1$。求解 $i$ 即找出变换 $i$,当其应用两次的时候,1 变成 -1。
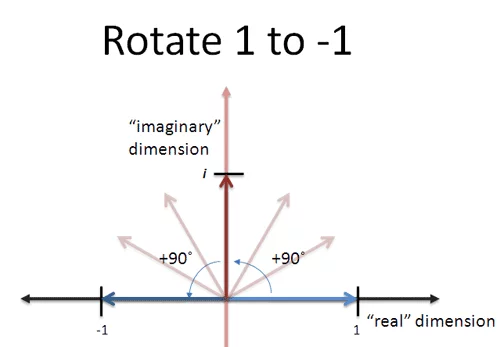
如上图,如果 $i$ 是旋转操作,每次逆时针旋转 90°,旋转两次,1 就会变成 -1。
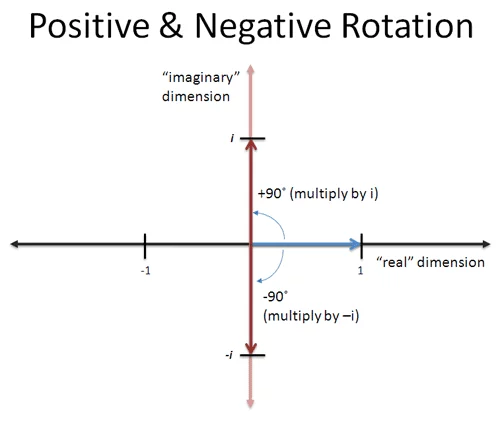
同理,顺时针旋转两次 90°,1 也会变成 -1。
我们可以这么来理解虚数 $i$:
- $i$ 用来衡量数字的“虚数维度”
- 乘以 $i$ 是逆时针旋转 90°,乘以 $-i$ 是顺时针旋转 90°
- 两次旋转无论是顺时针还是逆时针,结果都是 $-1$:它将我们带回到正负数的“常规”维度中
从这个角度理解,数字是二维的。
Understanding Complex Numbers
考虑下图:
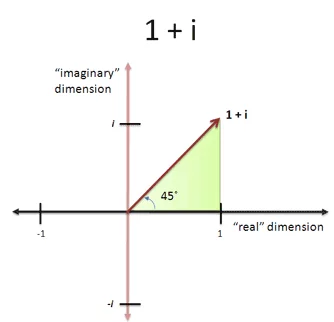
旋转 45°,实数和虚数部分相等:$1 + i$。
实际上,我们可以选择任意实数和虚数的组合,并构成一个三角形。这个角度成为了“旋转角度”。复数是同时具有实部和虚部的数的术语。它们的写法是 $a + bi$,其中:
- $a$ 是实部
- $b$ 是虚部
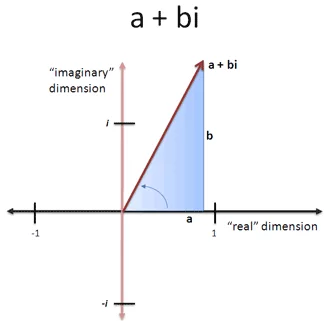
复数的大小即斜边于零的距离:
\[\text{Size of}\ a + bi=\sqrt{a^2+b^2}\]A Real Example: Rotations
乘以一个复数,即是按照其角度进行旋转。
假设我在一艘船上,每向北航行 4 个单位,就向东航行 3 个单位。我想将航向逆时针旋转 45°,新的航向是什么?
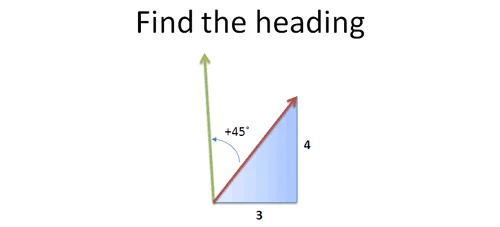
有了复数之后,不需要再用 sine、cosine 去计算,有更简单的计算方法:
当前的航向是 $3 + 4i$,想要将其旋转 45°。45° 可以表示为 $1 + i$,所以我们可以将这两个复数相乘其乘:
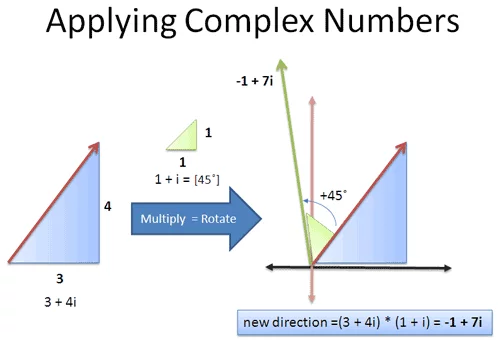
欧拉公式
欧拉公式 $e^{ix} = \cos x + i \sin x$ 的推导:
将 $i$ 代入泰勒级数:
\[e^x=\sum^{\infty}_{n=0}\frac{x^n}{n!}=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{x!} + ...\]得到:
\[e^{ix}=1+ix+\frac{(ix)^2}{2!}+\frac{(ix)^3}{3!}+\frac{(ix)^4}{x!} + ...\]因为 $i^2=-1$,级数简化成:
\[e^{ix}=1+ix-\frac{x^2}{2!}-\frac{ix^3}{3!}+\frac{x^4}{x!} + ...\]把含有 $i$ 和不含 $i$ 的项分开,得到:
\[e^{ix}=(1-\frac{x^2}{2!}+\frac{x^4}{x!})+i(x-\frac{x^3}{3!}+\frac{x^5}{x!})...\]左边是 $\cos$ 的泰勒级数,右边是 $\sin$ 的泰勒级数,因此 $e^{ix} = \cos x + i \sin x$。
把欧拉公式放到图上便会形成一个圆形:
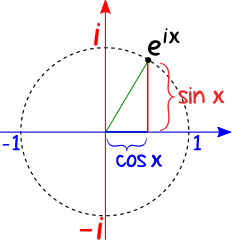
可以把任何点(例如 $3 + 4i$)变成 $re^{ix}$ 的格式(只需找到 $x$ 的值和圆形的半径 $r$)。以 $3 + 4i$ 为例,需要转换笛卡尔坐标为极坐标:
\[r = \sqrt{3^2+4^2} = 5\] \[x = \tan^{-1}(4/3) = 0.927\]