对 Transformer 中使用的位置编码的解读,分享两篇不错的文章:
- Why Are Sines and Cosines Used For Positional Encoding?
- Transformer Architecture: The Positional Encoding
本文为读书笔记。
Why Are Sines and Cosines Used For Positional Encoding?
Transformers and Self-Attention
对于每个输入向量 $\bf{x}$,计算三个新向量:查询向量 $\bf{q}$,键向量 $\bf{k}$ 和值向量 $\bf{v}$。然后计算 $\bf{x_{out}}$:
\[\bf{x_{out}} = (\bf{q}\cdot\bf{k_1})\bf{v_1}+(\bf{q}\cdot\bf{k}_2)\bf{v_2}+...+(\bf{q}\cdot\bf{k_n})\bf{v_n}\]这里的问题是没有考虑到输入的位置信息。两个向量在输入序列中的相对位置无论近远,点积始终相同。需要将位置信息纳入考虑。
Encoding Positions
假定 $\bf{x}_m$ 是位于位置 $m$ 的二维向量。我们可以将其表示为一个复数:
\[x_m = |x_m|e^{i\theta_m}\]定义 $f(x, m)$ 为位置编码函数,我们期待 $f$ 具有以下性质:
当将 $f$ 应用于两个向量以编码位置信息,并且计算这两个编码后的向量的点积时(注意力机制),我们希望结果取决于两个向量之间的距离,即 $m - n$,而不是取决于 $m$ 和 $n$ 本身,即:
\[f(x_m)\cdot f(x_n) = g(x_m,x_n,m-n) \tag{1}\]Exponentials
指数函数具有一个与我们所需类似的性质:
\[e^me^n=e^{m+n}\]沿着这个思路,但我们不希望直接用 $x_m$ 乘以 $e^m$,因为这会导致 $f$ 的大小随着位置 $m$ 的增加而迅速增长。我们尝试将其乘以 $e^{im\theta}$,因为它的大小是单位的(见虚数和复数),不会改变向量的幅度。因此 $f$ 定义如下:
\[f(x_m,m)=x_me^{im\theta}\]这里 $f$ 用乘法而不是更复杂的函数的原因是 Transformer 的网络结构中,$\bf{q}$、$\bf{k}$、$\bf{v}$ 向量都是输入向量的线性变换,如果 $f$ 也是其输入的线性变换,那么网络可能更容易学习。
由复数点积公式(见 https://proofwiki.org/wiki/Definition:Dot_Product/Complex):
\[x_m \cdot x_n = \Re[x_{m}x^\star_n]\]验证 $f$ 是否符合性质(1):
\[\begin{aligned}f(x_m)\cdot f(x_n) &= \Re{[x_mx_n^*e^{i(m-n)\theta}]}\\ &=\Re{[|x_m||x_n|e^{i(\theta_m-\theta_n+[m-n]\theta)}]}\\ &=|x_m||x_n|\cos(\theta_m-\theta_n+[m-n]\theta)\end{aligned}\]可见 $f$ 符合性质(1):编码后的结果仅仅是 $m-n$ 的函数,而不是单单取决于 $m$ 或 $n$。
From Exponentials to Sinusoidal Functions
现在我们有了一个候选的 $f$ 函数,如果 $\bf{x}$ 不是表示为复数,而是两个实数的向量呢?将一个复数乘以 $e^{i\theta}$ 等同于将其分量与一个旋转矩阵相乘:
\[\begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix}\]可以将这个思路扩展到更一般情况:将维度分成一对一对的,并对每对应用二维变换。
这里还有另一个问题。由于 $f$ 被定义为乘以一个周期函数,会导致不同距离的点具有相同的表示。如果将 $\theta$ 设定得非常大,网络可以轻松区分彼此更近的位置,但无法区分更远的位置;而如果将 $\theta$ 设定得非常小,则靠近的位置可能无法在 $f$ 中产生足够的变化使网络能够轻松区分它们。
处理这个问题的一种方法是为每对维度使用不同的 $\theta$ 值:一些维度编码较短距离的信息,而一些维度编码较长距离的信息。将所有这些综合起来,我们得到以下的变换形式:
\[f(\mathbf{x}, m) = \mathbf{x}\begin{pmatrix} \cos m\theta_1 & -\sin m\theta_1 & 0 & 0 & \cdots & 0 & 0 \\ \sin m\theta_1 & \cos m\theta_1 & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cos m\theta_2 & -\sin m\theta_2 & \cdots & 0 & 0 \\ 0 & 0 & \sin m\theta_2 & \cos m\theta_2 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & \cos m\theta_{d/2} & -\sin m\theta_{d/2} \\ 0 & 0 & 0 & 0 & \cdots & \sin m\theta_{d/2} & \cos m\theta_{d/2} \end{pmatrix}\]Transformer Architecture: The Positional Encoding
作者先对比了两种可能的方案:
- 方案一:给每个时间步分配一个[0,1]之间的数字。缺点是时间步的差异在不同长度的句子中的含义不一致。
- 方案二:线性地为每个时间步分配一个数字。如:第一个单词被赋予 “1”,第二个单词被赋予 “2”,依此类推。这种方法的问题是,数值可能变得非常大,且模型可能会遇到比训练中更长的句子,也可能不会遇到特定长度的样本,这会影响模型的泛化能力。
理想情况下,位置编码函数应满足以下几个条件:
- 对于每个时间步(单词在句子中的位置),应输出唯一的编码
- 在长度不同的句子中,任意两个时间步之间的距离应保持一致
- 我们的模型应能够轻松地泛化到更长的句子上,其数值应受到限制
- 位置编码必须是确定性的,即对于相同的时间步,始终产生相同的编码
作者以二进制为例:

观察不同位之间的变化速率。最低有效位在每个数字上交替变化,次低位在每两个数字上旋转,依此类推。
而浮点数使用二进制值会浪费空间。可以使正弦函数。与二进制中的交替位类似,正弦函数的值也会在不同的点上交替变化。调整正弦函数的频率能模拟二进制的频率变化。
作者还简短的证明了论文中的这段描述:
We chose this function because we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset $k$, $PE_{pos+k}$ can be represented as a linear function of $PE_{pos}$.
有兴趣可以读下原文,详细的证明见 Linear Relationships in the Transformer’s Positional Encoding。
线性转换的性质使模型能够轻松地学习相对位置的信息。
最后,作者还讨论了位置编码与 embedding 为什么是直接 sum 而不是进行 concat。
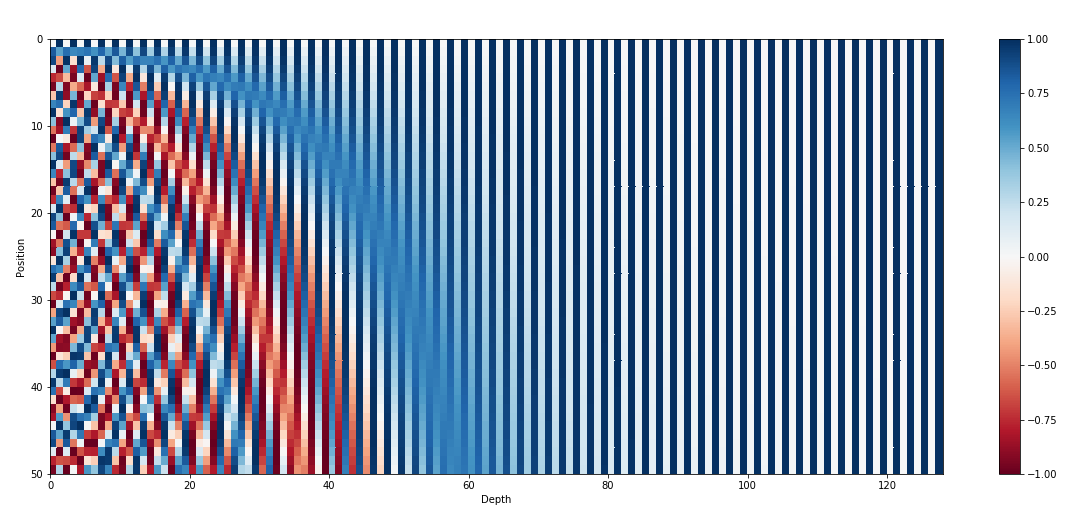
作者认为 embedding 只需要保留前面的维度存储位置信息就足够了(见上图)。如果使用 concat,维度更高,可能会稀释词嵌入中的语义信息。通过 sum 的方式,模型可以在组合嵌入的较低维度中保留单词的原始语义含义。