本文简单介绍 MoE 的发展历程和 DeepseekMoE 所做的优化。
Aaptive Mixtures of Local Experts
1991年,混合专家模型(MoE)的创始论文 Adaptive Mixtures of Local Experts 发布。论文提出一个由许多独立网络组成的系统,每个网络学习完整训练集的一个子集。这种学习过程可以将任务划分为适当的子任务,每个子任务都可以由一个非常简单的专家网络来解决。
使用反向传播来训练单个多层网络,在不同场合执行不同子任务,通常会出现强烈的干扰效应,导致学习缓慢且泛化能力差。如果事先知道一组训练案例可以自然地划分为对应不同子任务的子集,那么可以通过使用由几个不同的“专家”网络和一个决定每个训练案例应使用哪个专家的门控网络来减少干扰。这个思想之前已经有人实现过,其思想是使用门控网络将新的案例分配给一个或几个专家,如果输出不正确,权重的变化将局限于这些专家(和门控网络)。因此,对于专门处理完全不同案例的其他专家的权重不会产生干扰。一个专家的权重与其他专家的权重是解耦的,每个专家通常只被分配到可能输入向量空间的一个小局部区域。从这个意义上说,各个专家是局部化的。
但之前的系统使用了一个不鼓励局部化的误差函数:
\[E^c=||\mathbf{d}^c-\sum_{i}p_{i}^{c}\mathbf{o}_{i}^{c}||^{2}\]其中 $\mathbf{o}_i^c$ 是专家 $i$ 在案例 $c$ 上的输出向量,$p_i^c$ 是专家 $i$ 对组合输出向量的比例贡献,$\mathbf{d}^c$ 是案例 $c$ 中的期望输出向量。
这个误差函数将期望输出与局部专家输出的混合进行比较。当一个专家的权重发生变化时,剩余误差也会发生变化,因此所有其他专家的误差导数也会发生变化。这种专家之间的强耦合使它们能够良好地合作,但往往会导致每个案例使用到许多专家。一个更简单的解决方法是重新定义误差函数,以鼓励局部专家之间的竞争而不是合作。
设想门控网络随机决策使用哪个专家(见下图):
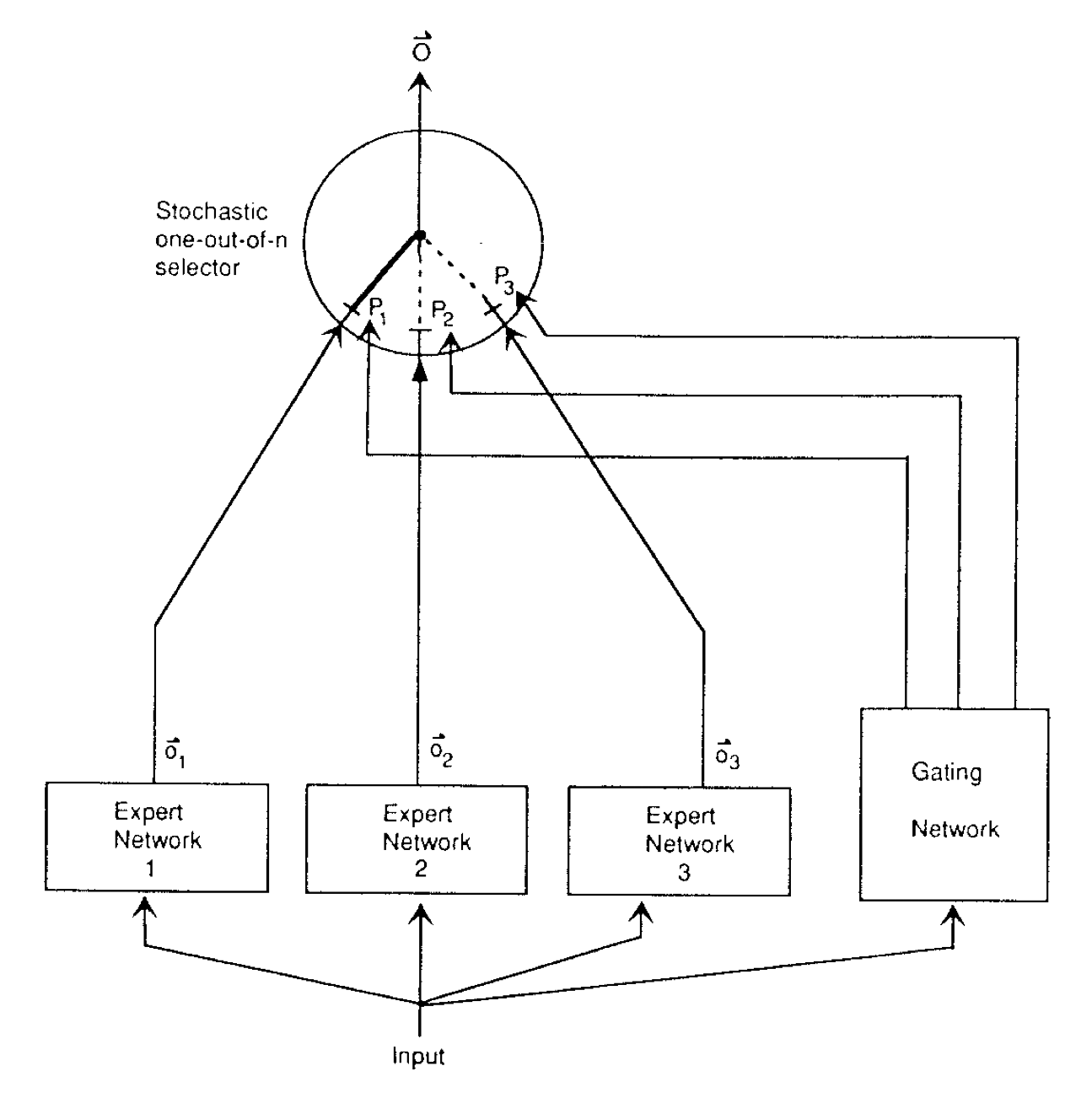
误差是期望值,即期望输出向量与实际输出向量之间的平方差的差异:
\[E^{c}=\langle||d^{c}-\mathbf{o}_{i}^{c}||^{2}\rangle=\sum_{i}p^c_i||d^{c}-\mathbf{o}_{i}^{c}||^{2}\]请注意,在这个新的误差函数中,每个专家需要生成整个输出向量。因此,对于给定的训练案例,局部专家的目标不会直接受到其他局部专家内部权重的影响。这里仍然存在一些间接的耦合,因为如果其他专家改变其权重,可能会导致门控网络改变分配给专家的责任,但至少这些责任变化不能改变局部专家在给定训练案例上感知到的误差的正负性。如果门控网络和局部专家都在这个新的误差函数中通过梯度下降进行训练,系统倾向于分配单个专家给每个训练案例。每当一个专家的误差小于所有专家误差的加权平均(由门控网络的输出来决定如何加权每个专家的误差),它对该案例的责任就会增加。
GShard
GShard 首次将 MoE 引入到 Transformer 架构中,将前馈层替换为 Position-wise Mixture of Experts (MoE) 层,并在编码器和解码器中使用 top-2 门控变体(见下图):
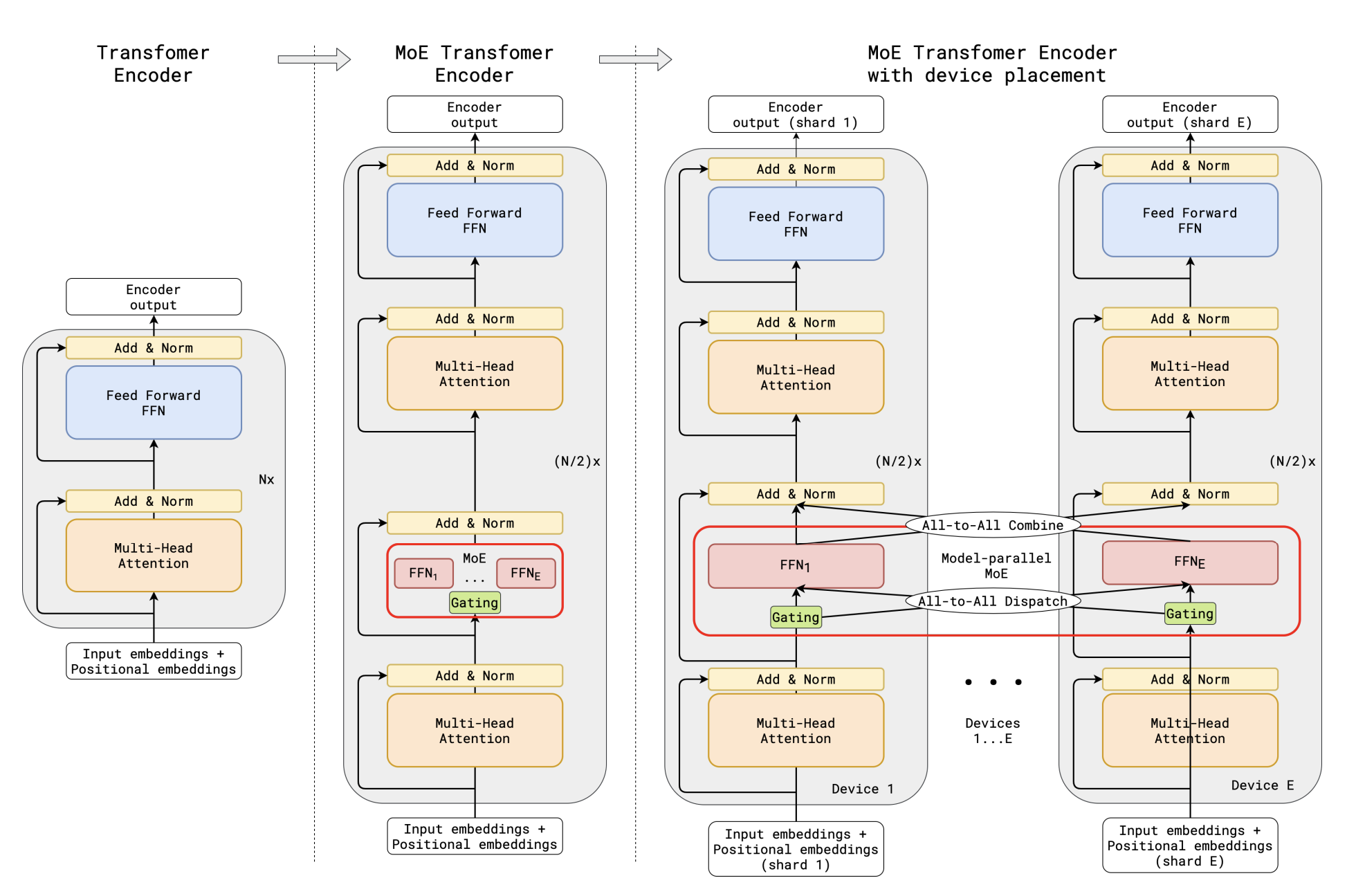
用 MoE 层替换每隔一个的 Transformer 前馈层。解码器的修改类似。(a) 标准 Transformer 模型的编码器是由自注意力和前馈层交错组成的堆栈,并配有残差连接和层归一化。(b) 通过将每隔一个前馈层替换为 MoE 层,我们得到了 MoE Transformer 编码器的模型结构。(c) 当扩展到多个设备时,MoE 层在设备之间分片,而所有其他层则被复制。
Transformer 中的 MoE 层由 $E$ 个前馈网络 $\text{FFN}_1 . . . \text{FFN}_E$ 组成:
\[\begin{array}{c} \mathcal{G}_{s,E}=\mathrm{GATE}(x_{s})\\ \mathrm{FFN}_{e}(x_{s})=w o_{e}\cdot\mathrm{ReLU}(w i_{e}\cdot x_{s})\\ y_{s}=\sum_{e=1}^{E}\mathcal{G}_{s,e}\cdot\mathrm{FFN}_{e}(x_{s}) \end{array}\]向量 $\mathcal{G}_{s,E}$ 是由一个门控网络计算得出的,每个专家都有一个非负值,表示专家对最终网络输出的贡献程度,为零表示该 token 未分派给该专家。我们选择让每个 token 最多分派给两个专家。MoE 层的输出 $y_s$ 是从所有选定的专家的输出加权平均得到的。
Switch Transformers
Switch Transformers 优化了 MoE 路由算法,降低通信和计算成本。
Switch Transformer 的设计原则是以简单和高效的方式最大化 Transformer 模型的参数数量。在 Kaplan 等的研究中,发现模型规模、数据集大小和计算预算之间存在幂律扩展(power-law scaling)的关系。基于这些结果,作者研究了第四个维度:增加参数数量,同时保持每个示例的浮点运算(FLOPs)恒定。作者通过设计一个稀疏激活的模型来实现这一点。
与其他人采用的 TopK 策略不同,Switch Transformers 使用了一种简化的策略,只将输入路由到单个专家。这种 k = 1 的路由策略被称为 Switch 层。见下图:
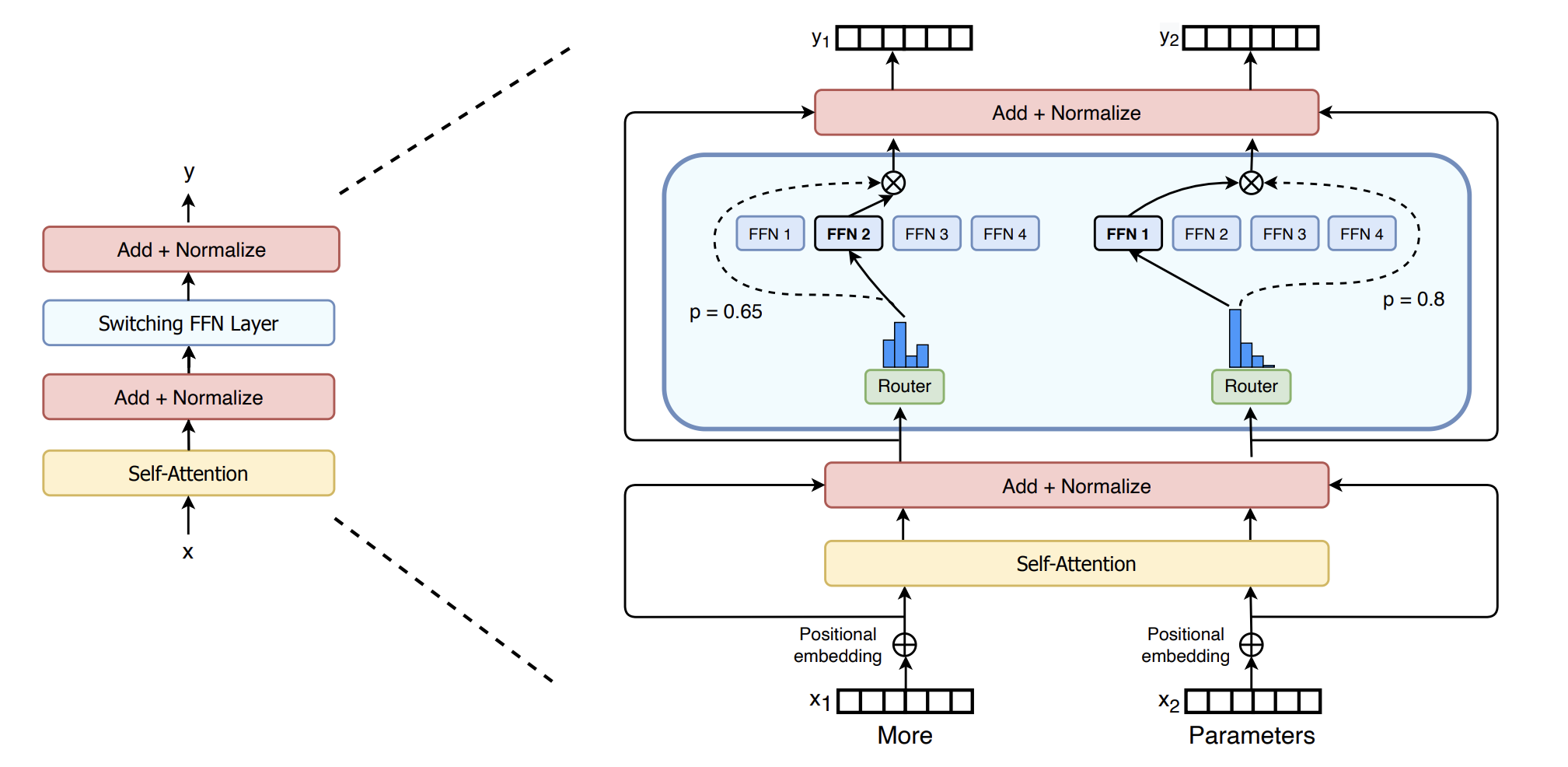
用稀疏的 Switch FFN 层(浅蓝色)替换了 Transformer 中的密集 FFN 层。该层独立地对序列中的 token 进行操作,以两个 token 为例,展示它们通过四个 FFN 专家进行路由(实线),其中路由器独立地对每个 token 进行路由。Switch FFN 层返回所选 FFN 的输出乘以路由器门控值(虚线)。
Switch 层的好处有三个:
- 由于只将标记路由到单个专家,路由计算量减少了
- 每个专家的批量大小(专家容量)可以至少减半,因为每个标记只被路由到单个专家
- 简化了路由的实现,减少了通信成本
专家容量(即每个专家计算的 token 数)通过将批量中的 token 数量均匀分配给专家,然后再乘以一个容量因子进行扩展,如下图:
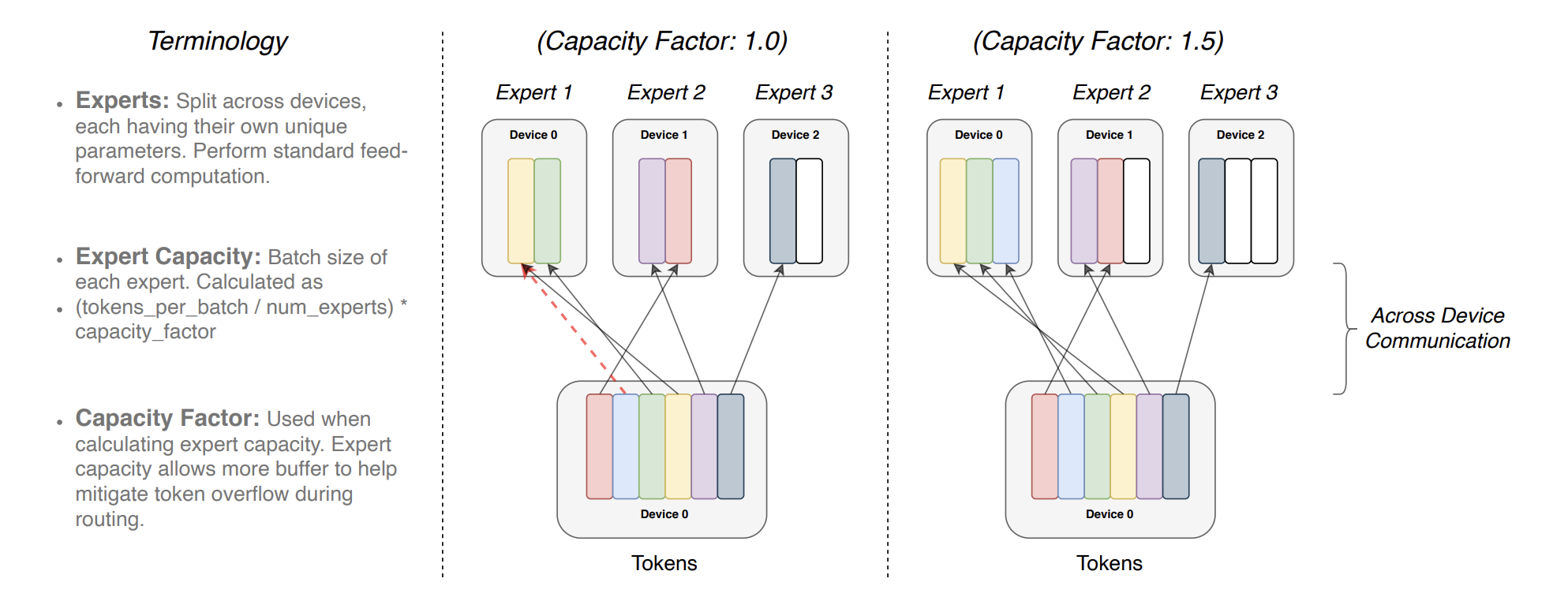
图3:每个 token 被路由到具有最高路由概率的专家,但每个专家的批量大小固定。如果 token 分配不均,则某些专家将溢出(用虚线的红线表示),导致这些 token 不会被该层处理。较大的容量因子可以缓解溢出,但也会增加计算和通信成本(用白色空槽表示)。
确保较低的 token 丢弃率对于稀疏专家模型的扩展非常重要,使用足够高的辅助负载平衡损失系数可以确保良好的负载平衡。辅助负载平衡损失定义如下:
\[\mathrm{loss} = \alpha \cdot N \cdot \sum_{i=1}^{N} f_{i} \cdot P_{i}\]其中 $N$ 为专家数量,$f_{i}$ 是分配给专家 $i$ 的 token 的比例,$P_{i}$ 是路由到专家 $i$ 的概率比例。
DeepseekMoE
传统的 MoE 架构(如 GShard)在确保专家专业度(即每个专家获取非重叠且专注的知识)上存在挑战。 论文提出 DeepSeekMoE 架构以实现专家专业化,其涉及两个主要策略:
- 将专家细分为 $mN$ 个,并从中激活 $mK$ 个,允许更灵活地组合激活的专家
- 将 $K_s$ 个专家作为共享专家进行隔离,旨在捕捉共享知识并减少路由专家中的冗余
主要解决以下两个问题:
- 知识混合性:现有 MoE 实践通常使用有限数量的专家(如8或16),导致分配给特定专家的 token 可能涵盖多样化知识
- 知识冗余:分配给不同专家的 token 可能需要共同知识,导致多个专家在各自参数中共享了知识,出现知识冗余
细粒度的专家分割可以更精细地分解多样化的知识,并更精确地学习到不同的专家中,每个专家将保持更高水平的专业化。将共享知识压缩到这些共享专家中可以减轻其他路由专家之间的冗余,提高了参数效率。
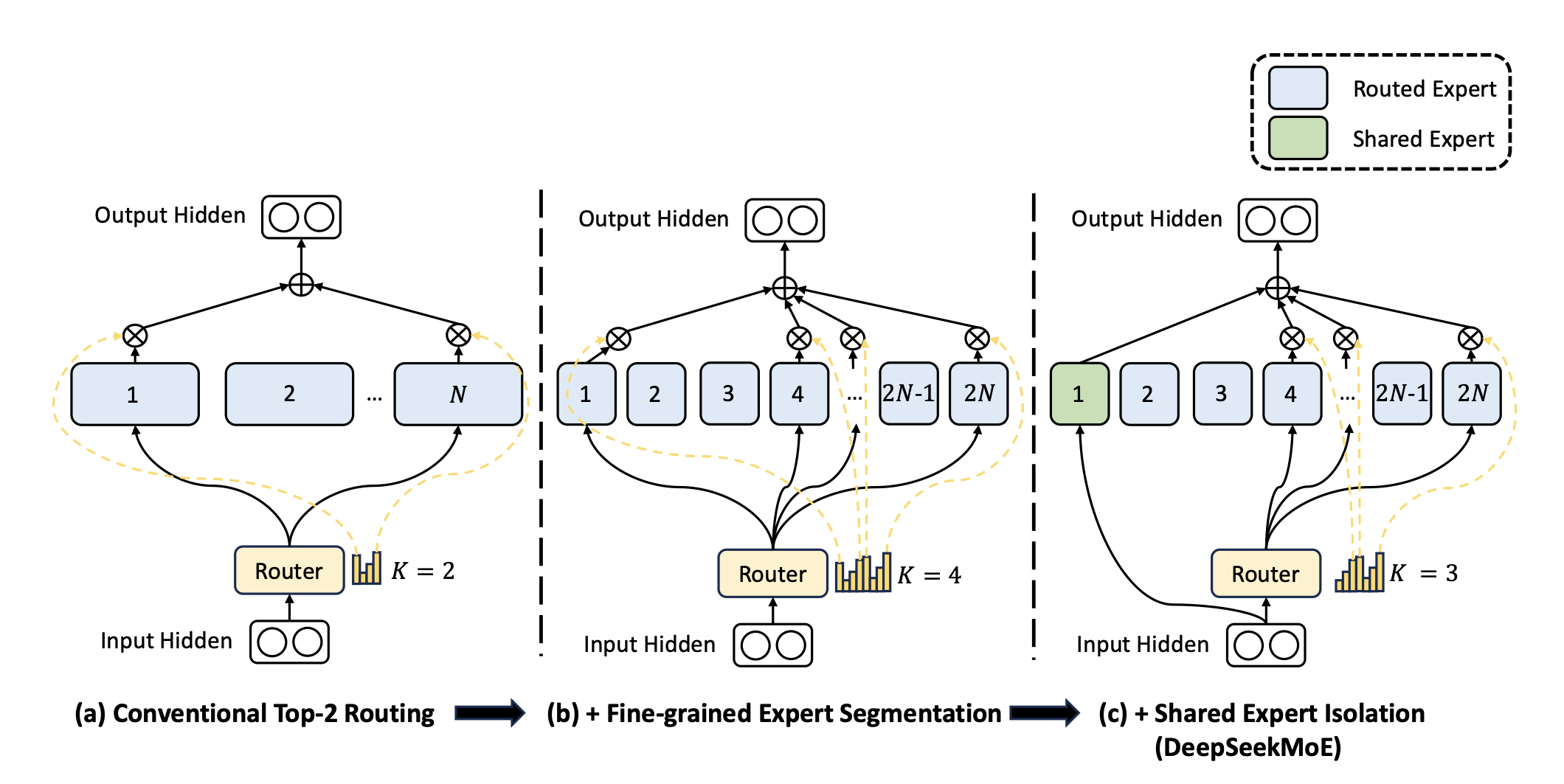
子图(a)展示了具有传统的前 2 路由策略的 MoE 层。子图(b)说明了细粒度专家分割策略。随后,子图(c)展示了共享专家隔离策略的集成,构成了完整的 DeepSeekMoE 架构。在这三种架构中,专家参数的数量和计算成本保持不变。
在上图 (a) 所示的典型 MoE 架构的基础上,通过将 FFN 中间隐藏维度减小为原始大小的 1/m,将每个专家的 FFN 分割为 m 个较小的专家。由于每个专家变小,为了保持相同的计算成本,将激活的专家数量增加到 m 倍,如上图 (b)所示。从组合的角度来看,细粒度专家分割策略极大地增强了激活专家的组合灵活性。以 $N = 16$ 为例,典型的 top-2 路由策略可以产生 ${16 \choose 2}= 120$ 种可能的组合。相比之下,如果每个专家被分成 4 个小专家,细粒度路由策略可以产生 ${64 \choose 8}= 4,426,165,368$ 种潜在的组合,提高了实现更准确和有针对性的知识获取的潜力。
除此之外,DeepseekMoE 进一步隔离出 $K_s$ 个专家作为共享专家。每个 token 都将被确定性地分配给这些共享专家。为了保持恒定的计算成本,其他路由的专家中激活的专家数量将减少 $K_s$ 个,如上图(c)所示。
自动学习的路由策略可能会遇到负载不平衡的问题,会表现出两个明显的缺陷。首先,存在路由崩溃的风险,即模型总是只选择少数几个专家,阻止其他专家得到充分的训练。其次,如果专家分布在多个设备上,负载不平衡可能会加剧计算瓶颈。
为了减轻路由崩溃的风险,DeepseekMoE 采用了专家级平衡损失。平衡损失的计算如下:
\[\mathcal{L}_{\text{ExpBal}}=\alpha_{1}\sum_{i=1}^{N^{\prime}}f_{i}P_{i} \\ f_{i}=\frac{N^{\prime}}{K^{\prime}T}\sum_{t=1}^{T}\mathbb{1}\,(\text{Token $t$ selects Expert $i$}) \\ P_{i}=\frac{1}{T}\sum_{t=1}^{T}s_{i,t}\]这里 $\alpha_{1}$ 为专家级平衡因子,$N^{\prime} = (mN-K_s)$ 为路由的专家个数,$K^{\prime} = mK - K_s$ 为激活的路由专家个数,乘以 $\frac{N’}{K’}$ 是为了归一化,使 loss 的计算和专家的数量解耦。$\mathbb{1}\,(·)$ 表示指示函数(indicator function),$s_{i,t}$ 表示 token 与专家之间的关联度。
除了专家级平衡损失,DeepseekMoE 还引入了设备级平衡损失。旨在缓解计算瓶颈时,没有必要在专家级别强制执行严格的平衡约束,因为过度的负载平衡约束会损害模型性能。相反主要目标是确保设备间的计算平衡。如果将所有路由的专家分成组 ${\mathcal{E}_1, \mathcal{E}_2, …, \mathcal{E}_D}$,并将每组部署在一个单一设备上,设备级平衡损失的计算如下:
\[\mathcal{L}_{DevBal} = \alpha_{2} \sum_{i=1}^{D} f_i^{\prime} P_{i}^{\prime} \\ f^{\prime}_i = \frac{1}{|\mathcal{E}_i|}\sum_{j \in \mathcal{E}_i}f_j \\ P'_i = \sum_{j \in \mathcal{E}_i}P_j\]其中 $\alpha_{2}$ 为设备级平衡因子。实践中 DeepseekMoE 设置一个较小的专家级平衡因子来减轻路由崩溃的风险,同时设置一个较大的设备级平衡因子来促进设备间的计算平衡。