Deepseek DualPipe 主要是结合了 Chimera 和 Zero Bubble 这两篇论文的思想。本文是这两篇论文的笔记。
Chimera
INTRODUCTION
Chimera: Efficiently Training Large-Scale Neural Networks with Bidirectional Pipelines 提出了名为 Chimera 的新型流水线并行方案,用于高效地训练大规模模型。Chimera 采用同步方法,因此不会出现精度损失,这比异步方法更有利于收敛。与最新的同步流水线方法相比,Chimera 将气泡数量减少了多达 50%;得益于双向流水线的精细调度,Chimera 具有更平衡的激活内存消耗。
深度神经网络由分层架构组成,可以通过两种方式实现分布式:
- 操作符并行化(operator parallelism):一层的操作符可以在多个加速器之间进行分割
- 流水线并行化(pipeline parallelism):将模型逐层分布
操作符并行化对于每个基本 Transformer 层的输出激活需要两个 all-reduce 操作。另一方面,使用逐层模型划分,流水线并行化只需要 p2p 通信来在流水线阶段之间传输输出激活,每个阶段包含一组连续的层。因此,与操作符并行化相比,流水线并行化通常具有更低的通信成本。然而,流水线并行化存在气泡或权重滞后的问题。总体而言,操作符并行化和流水线并行化在分布大型深度学习模型方面是正交且互补的。
流水线并行化并不简单:反向传播算法需要“记住”在前向传递期间计算的输出激活作为反向传递的输入,这导致流水线中的每个加速器有完全不同的内存需求,即使每个加速器的计算负载是相同的。最近提出的流水线方法,如 DAPPLE、PipeDream 和 PipeDream2BW,深度为 $D$ 的流水线的第一个加速器必须存储 $D$ 个这样的激活,而最后一个加速器只需要存储一个激活(见图 1)。这不仅导致流水线后续阶段的内存利用率降低,还会降低性能,因为微批次大小必须适应流水线中的第一个加速器。这种不平衡可以通过限制同时允许在流水线中的微批次数量来缓解。然而,这会引入气泡并限制整体系统利用率。
微批次大小和流水线利用率对计算效率非常重要:较大的微批次由于在类似矩阵乘法的操作中更好地重用,可以提高性能,而较少的流水线气泡可以更好地利用加速器。计算效率直接关系到训练模型的成本和时间。
BACKGROUND AND RELATED WORK
为了获得更好的收敛质量,同步方法在每个训练迭代结束时同步梯度并清空流水线,因此同步方法会导致流水线中的气泡。为了利用流水线,GPipe 同时将 N 个微批次注入到流水线中;DAPPLE 用 One-Forward-One-Backward(1F1B)调度,并定期清空流水线。GPipe 和 DAPPLE 都会产生 2(D-1) 个气泡(即前向传递中有 D-1 个气泡,后向传递中也有 D-1 个气泡)。实践中后向的工作量大约是前向的两倍,因此实际产生的气泡是 3(D-1),见图 1。
尽管 GPipe 和 DAPPLE 的气泡比率随着 N(每个工作节点在训练迭代中执行的微批次数量)的增加而减少,一个足够大的 N(建议 N>=4D),通常由于以下三个原因无法在不损害效率的情况下获得:
- 通常对于一个模型存在经验上的最大 $\hat{B}$(小批量大小),超过这个值会影响模型的收敛性
- 对于给定的 $\hat{B}$,增加 N 意味着,B(微批量大小)会减小。然而,现代加速器需要足够大的 B 才能实现高计算效率
- 对于给定的 $\hat{B}$,与数据并行化结合以扩展到大规模机器会减小 N
GEMS 是一种内存高效的流水线方法,它在两个模型副本之间调度微批次。由于 GEMS 主要设计用于较小的 $\hat{B}$,并且同时最多只有两个活跃的微批次,因此其气泡比率比其他方法高得多,并且无法通过增大 N 来缓解。
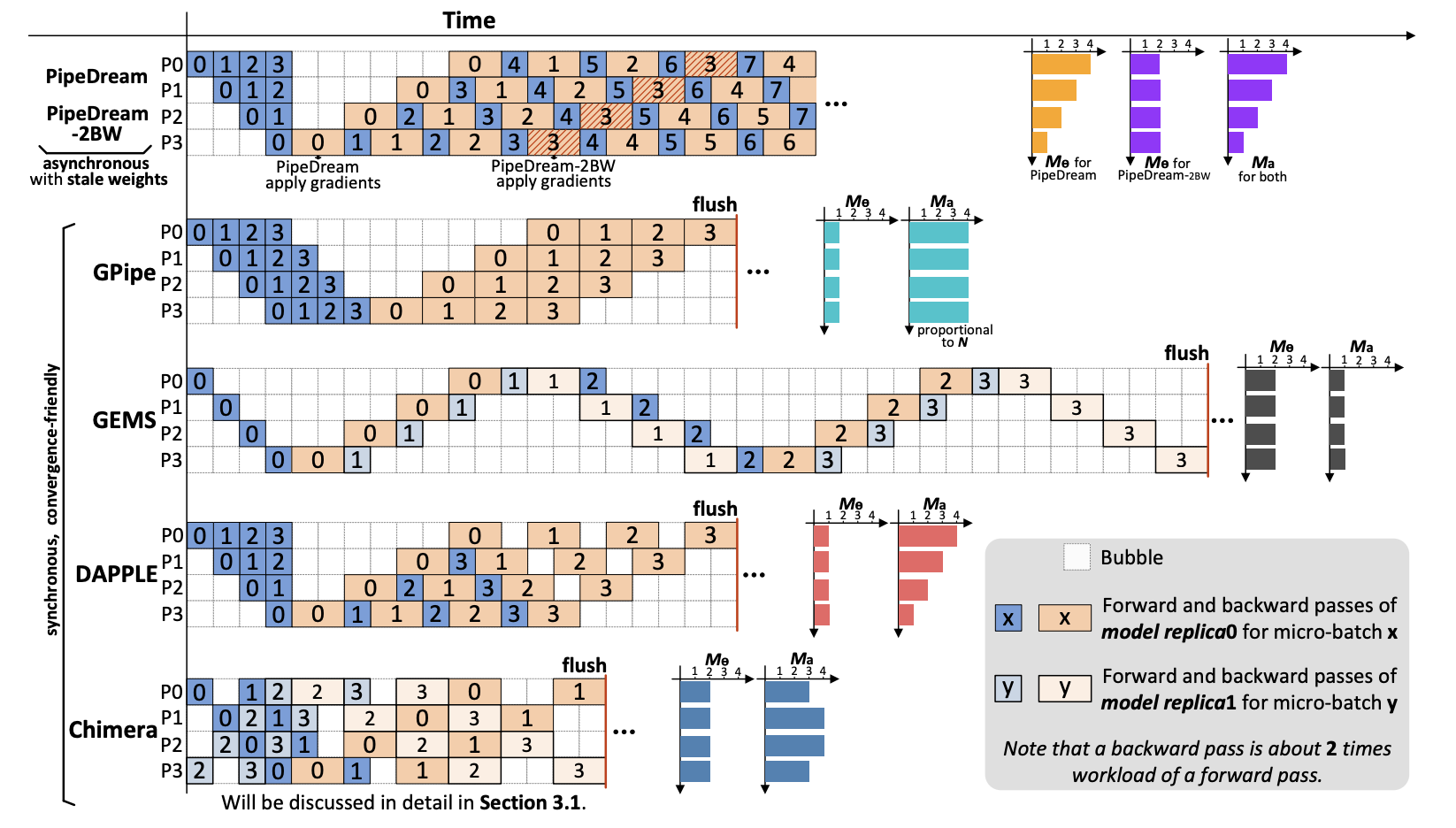
图1:流水线并行化方案中,每个训练迭代中有四个流水线阶段(D=4)和四个微批次(N=4),除了 PipeDream 在每个微批次的反向传递之后更新模型。
Chimera 通过运行完全填充的双向流水线,实现了以下功能:
- 在不依赖滞后权重的情况下保持整体训练同步
- 比现有方法具有更高的流水线利用率(更少的气泡),从而获得更高的性能
- 与最先进的方法相比具有相同的峰值激活内存消耗,且内存消耗更平衡
- 可以根据准确的性能模型轻松配置各种流水线深度神经网络和系统架构
和 GPipe 和 DAPPLE 相比,Chimera 产生 D-2 个气泡(即前向传递中有 D/2-1 个气泡,后向传递中也有 D/2-1 个气泡),减少了约 50%。
内存开销主要来自两个方面:权重参数和激活值(前向传递中的中间结果,在后向传递中用于计算梯度)。对于 GPipe 和 DAPPLE,每个工作节点维护一个流水线阶段的权重。对于 GEMS 和 Chimera,每个工作节点维护两个流水线阶段的权重,因为有两个方向的流水线。PipeDream 在每个微批次的后向传递之后更新模型,为了确保前向传递和后向传递之间的权重版本一致性,它需要在工作节点上存储多达 D 个版本的权重,这与纯数据并行化具有相同的内存成本。通过使用梯度累积,PipeDream-2BW 将需要存储的权重版本数量减少到 2 个。
ZeRO 通过在数据并行进程之间对三个模型状态(即优化器状态、梯度和参数)进行分区来消除内存冗余,虽然会略微增加通信量。需要注意的是,我们的流水线方法与 ZeRO 是相互独立的。
通过定期的流水线清空,同步方法确保在训练迭代中所有阶段和所有微批次使用相同版本的权重,而不会引入滞后性。从算法的角度来看,同步方法等同于标准且经过验证的小批量随机梯度下降,因此可以保证收敛性。而更近期的研究观察到,异步训练算法可能导致较低的收敛性能。
对于模型准确性,所有同步流水线方法(如Chimera、DAPPLE、GPipe和GEMS)都能保证达到与标准小批量随机梯度下降算法相同的准确性。对于异步方法(如PipeDream-2BW和PipeDream),由于引入了权重的陈旧性,无法像标准算法那样安全地达到理想的准确性,而收敛质量可能在不同的神经网络和任务上有所变化。
THE SCHEME OF CHIMERA
Bidirectional Pipelines
Chimera 的关键思想是将两个不同方向的流水线(分别称为下行流水线和上行流水线)组合在一起。图 2 展示了一个具有四个流水线阶段(即 D=4)的示例。在一个训练迭代中,我们假设每个工作节点执行 D 个微批次(N=D),这是保持所有流水线阶段活跃所需的最小值。在下行流水线中,stage0∼stage3 线性映射到 P0∼P3,而在上行流水线中,阶段的映射顺序完全相反。这 N个微批次在两个流水线之间均匀分配。每个流水线使用 1F1B 策略调度 N/2 个微批次,如图 2 左侧所示。然后,通过将这两个流水线合并在一起得到 Chimera 的流水线调度(图 2 右上方)。给定偶数个阶段 D,合并过程中保证没有冲突(即每个工作节点上同一时间槽最多只有一个微批次)。我们可以看到前向传递和后向传递中的空闲阶段数量分别减少到 D/2-1。通过考虑前向传递和后向传递之间的工作负载不均衡,我们得到了更实用的 Chimera 调度。
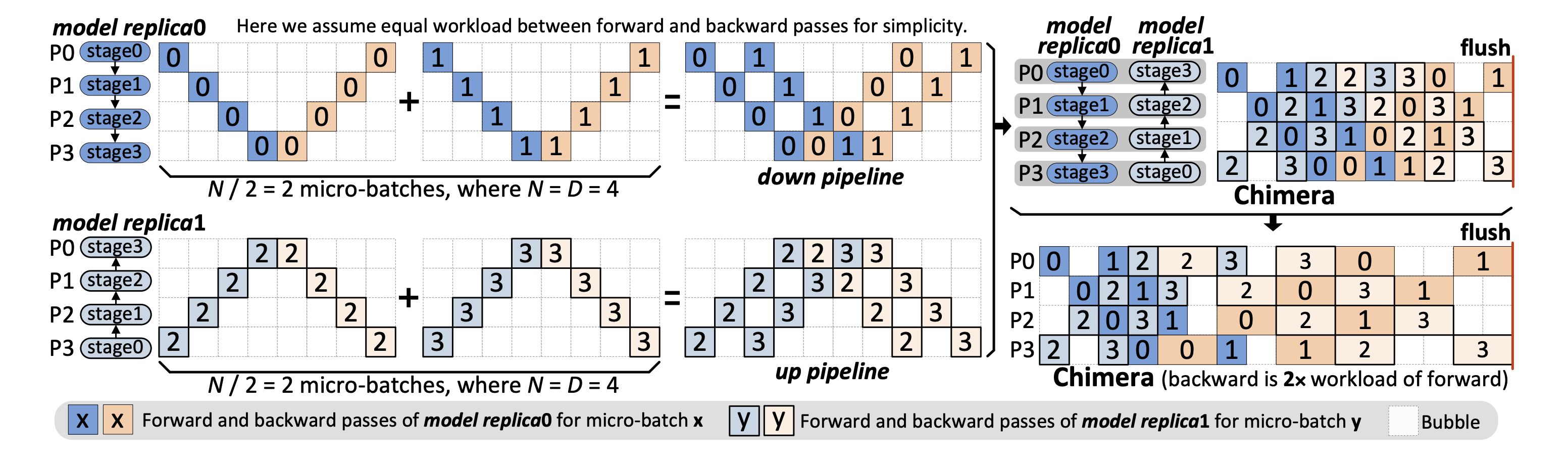
图2:Chimera的模型副本和双向流水线调度。
Communication Scheme
Chimera 使用点对点(p2p)通信在前向传递和后向传递中的流水线阶段之间传输中间激活和梯度(相对于输入)。由于 Chimera 将双向流水线组合在一起,集合通信(即 allreduce)用于在下一个训练迭代前同步阶段副本之间的权重梯度。图 3(a) 展示了一种简单的梯度同步方式,即在当前迭代的所有本地计算完成后,同步每个阶段由工作节点维护的梯度。需要注意到,中间阶段的梯度同步与开始和结束阶段的计算部分重叠。

图3:通过重叠隐藏梯度同步开销。
为了实现更深层次的通信重叠,可利用流水线中的空闲时间窗口,主动启动 allreduce 操作。以图 3(b) 中的 P0 和 P3 为例,在它们分别完成微批次 3 和微批次 1 的反向传播后,stage3 的权重梯度计算已经完成。因此,P0 和 P3 可以使用非阻塞的集合通信方式,在它们完成计算后立即启动异步的 allreduce 操作,以同步 stage3 的梯度,并在所有本地计算完成后调用等待操作,确保 allreduce 操作已经完成。通过这种方式,stage3 的梯度同步可以在空闲时间窗口和后续计算中重叠进行。然而与 P0 和 P3 不同,我们选择不在 P1 和 P2 上对 stage2(中间阶段)马上进行梯度同步,因为从 stage2 梯度计算完成到本地计算结束之间没有空闲时间窗口。尽管异步通信可以在计算进行时进行,但它可能会引入额外的开销(初始化、线程等),这可能会延长流水线的关键路径,影响整体性能。
Hybrid of Pipeline and Data Parallelism
Chimera 支持流水线并行和数据并行的混合模式。Chimera 的双向流水线被复制 W 次以适应 W·D 个工作节点。在混合并行中,所有的 D 个阶段复制 W 次。当扩展到配备高性能互连网络的并行计算机时,混合并行通常比纯粹的流水线并行获得更好的性能。这是因为纯粹的流水线并行中有 W·D 个阶段,而混合并行只有 D 个阶段(减少了 W 倍),这有助于减少阶段之间的点对点通信开销,并增加每个阶段的计算工作量。尽管混合并行会导致阶段副本之间的梯度同步,但通过前面提到的高性能互连网络可以减轻这种开销。
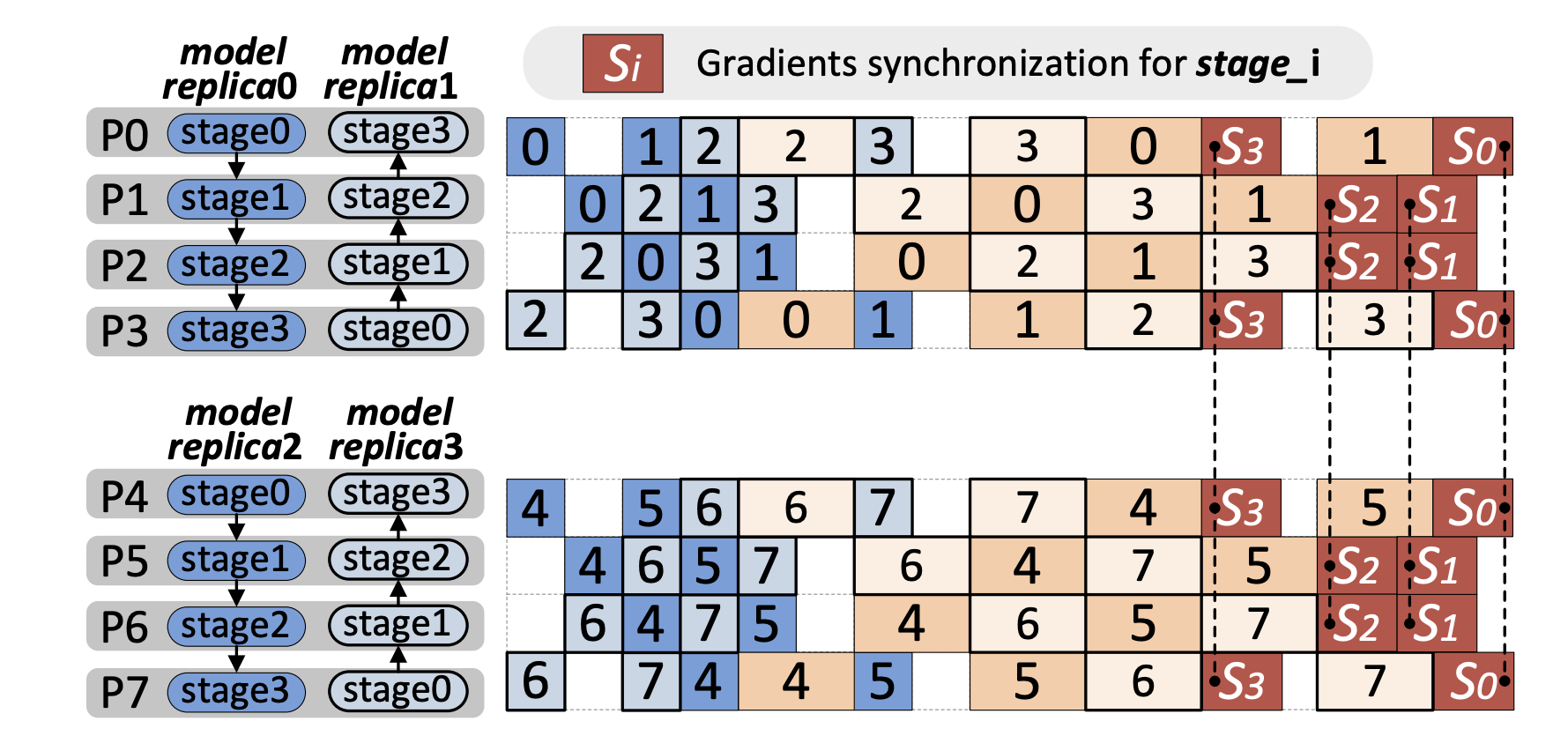
图4:在 Chimera 中将流水线并行和数据并行相结合(W = 2,D = 4)。
Zero Bubble Pipeline Parallelism
INTRODUCTION
Zero Bubble Pipeline Parallelism 引入了一种调度策略,是第一个在同步训练语义下成功实现零流水线气泡的方法。关键思想是将反向计算分为两部分,一部分计算输入的梯度,另一部分计算参数的梯度。
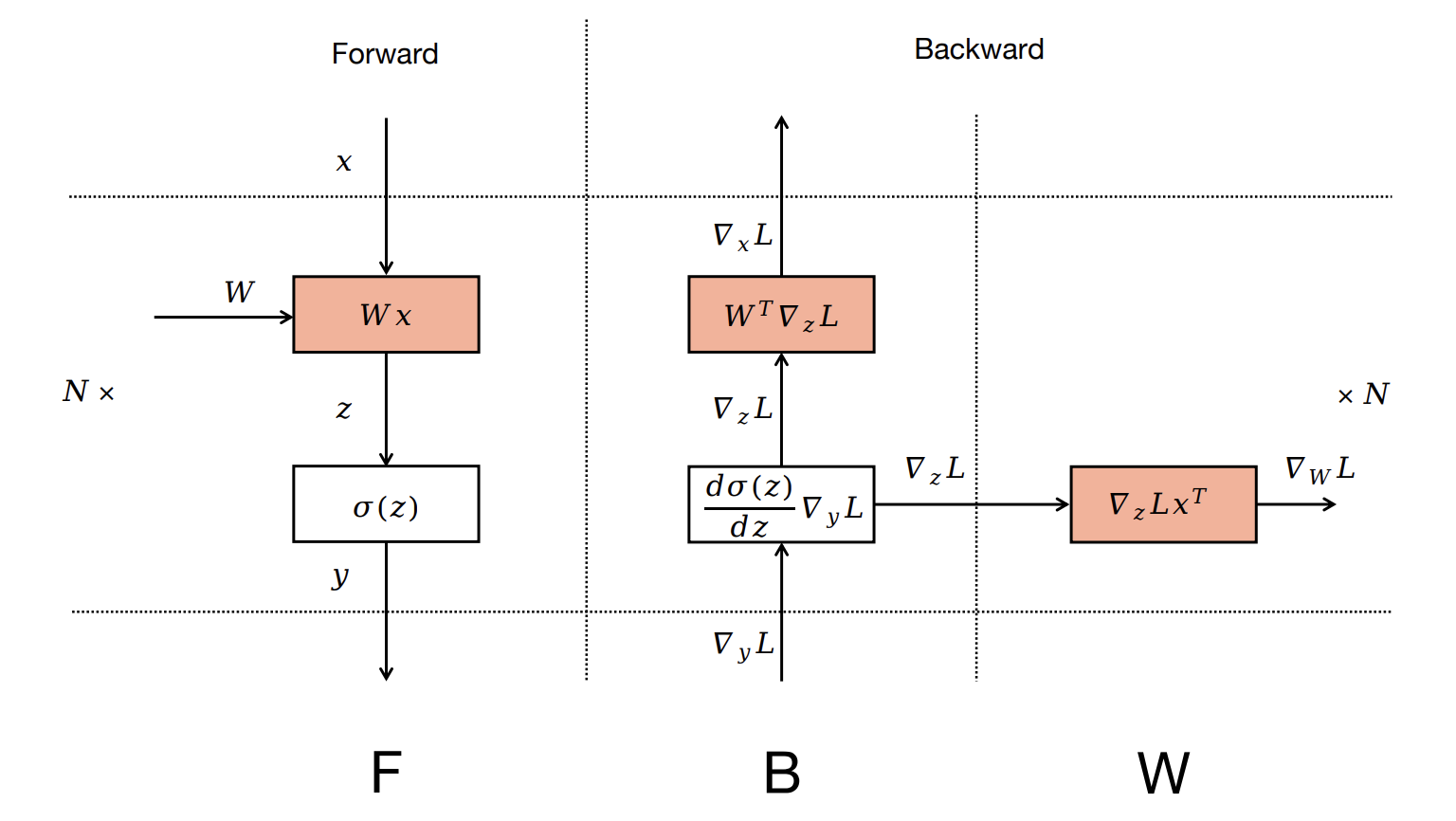
传统上,神经网络被划分为层。每个层与两个函数相关联,即前向传播和反向传播。在前向传播中,输入 $x$ 通过参数化映射 $f(x,W)$ 转换为输出 $y$。对于训练来说,反向传播至关重要,它涉及两个计算:$\nabla_x f(x,W)^{\top} \frac{dl}{dy}$ 和 $\nabla_W f(x,W)^{\top}\frac{dl}{dy}$,分别计算相对于输入 $x$ 和层参数 $W$ 的梯度。为方便起见,我们分别用单个字母 $B$ 和 $W$ 表示这两个计算,用 $F$ 表示前向传播。传统上,$B$ 和 $W$ 被组合并提供为单个反向传播函数。这种设计在概念上对用户友好,并且对于 DP 来说效果很好,因为在第 i 层,权重梯度的通信可以与第 i-1 层的反向计算重叠。然而,在 PP 中,这种设计不必要地增加了顺序依赖的计算,即第 i-1 层的 $B$ 依赖于第 i 层的 $W$,这通常有损效率。
基于将 $B$ 和 $W$ 分离可以减少顺序依赖性从而提高效率的关键观察,我们重新设计了从常用的 1F1B 调度开始的流水线。如下图所示,1F1B 从一个 warm-up 阶段开始。在这个阶段,工作节点进行不同数量的前向传播,每个阶段通常比其紧接的下一个阶段多进行一次前向传播。在热身阶段之后,每个工作节点进入稳定状态,交替执行一次前向传播和一次反向传播,确保各个阶段之间的工作负载均衡。在最后阶段,每个工作节点处理尚未完成的微批次的反向传播,完成整个批次的处理。

在我们改进的版本中,我们将反向传播分为 $B$ 和 $W$ 传播,必须确保同一微批次中的 $F$ 和 $B$ 仍然在流水线阶段之间保持顺序依赖。然而,$W$ 可以在相应阶段的 $B$ 之后的任何位置灵活调度。这允许策略性地安排 $W$ 以填充气泡。
HANDCRAFTED PIPELINE SCHEDULES
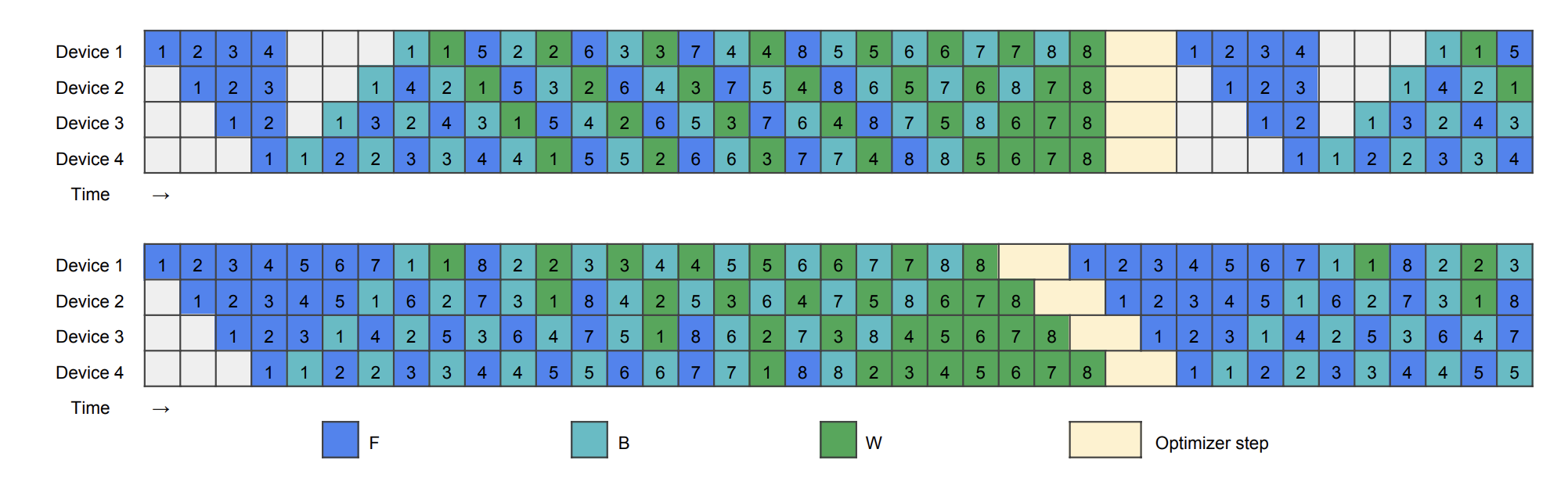
图7:手工设计的流水线调度,上:ZB-H1;下:ZB-H2
MEMORY EFFICIENT SCHEDULE
我们的第一个手工调度方案名为 ZB-H1,确保所有工作节点的最大峰值内存使用量不超过 1F1B 的峰值内存使用量。ZB-H1 遵循 1F1B 的调度,但根据 warm-up 微批次的数量调整了 $W$ 的起始点。这确保所有工作节点保持相同数量的正在处理的微批次。结果如图7(上)所示,气泡减小到 1F1B 的三分之一。这是因为与 1F1B 相比,$B$ 在所有工作节点上都提前启动,并且后期启动的 $W$ 传播填充了尾部的气泡。由于 $W$ 通常使用的内存比 $B$ 少,第一个工作节点的峰值内存使用量最大,与 1F1B 一致。
ZERO BUBBLE SCHEDULE
当允许占用比 1F1B 更大的内存,并且有足够数量的微批次时,可以实现零气泡调度,我们将其标记为 ZB-H2。如图7(下)所示,在热身阶段我们引入更多的 $F$ 传播来填充初始 $B$ 之前的气泡。我们还重新排序尾部的 $W$ 传播,将布局从梯形变为平行四边形,消除了流水线中的所有气泡。需要强调的是,在这里我们移除了优化器步骤之间的同步,下面讨论如何安全地实现这一点。
在大多数流水线并行实践中,为了保证数值稳定性,通常会在优化器步骤中进行流水线阶段之间的同步。例如,需要计算全局梯度范数以进行梯度范数裁剪;在混合精度设置中,需要对 NAN 和 INF 值进行全局检查;这两种情况都需要在所有阶段之间进行全局通信。从图 7 可以看到,在优化器步骤中进行同步会破坏平行四边形,使得零气泡变得不可能。我们提出了一种替代机制来绕过这些同步,同时仍然保持同步优化的语义。
在现有的实现中,首先启动一个 all-reduce 通信来收集全局状态,然后进行基于全局状态的优化器步骤。然而,我们注意到大多数情况下全局状态没有任何影响,例如对于 NAN 和 INF 的全局检查很少触发,因为在稳健的设置中,大多数迭代不应该出现数值问题;经验上梯度裁剪率也相当低,无法证明每次迭代都需要同步全局梯度范数。
基于以上观察,我们提出用后续更新验证替代预先的同步操作。如下图,在每个阶段的优化器步骤之前,从前一个阶段接收到部分 reduced 的全局状态,与当前阶段的局部状态结合,并传递给下一个阶段。每个阶段的优化器步骤由部分 reduced 的状态控制,例如,当发现 NAN 或部分归约的梯度范数超过裁剪阈值时,跳过更新。在下一次迭代的热身阶段,完全 reduced 的全局状态从最后一个阶段传播回第一个阶段。在接收到全局状态后,每个阶段执行验证以决定前一个优化器步骤是否合法。如果需要对梯度进行修正,则发出回滚操作,然后基于完全归约的全局状态重新执行优化器步骤。
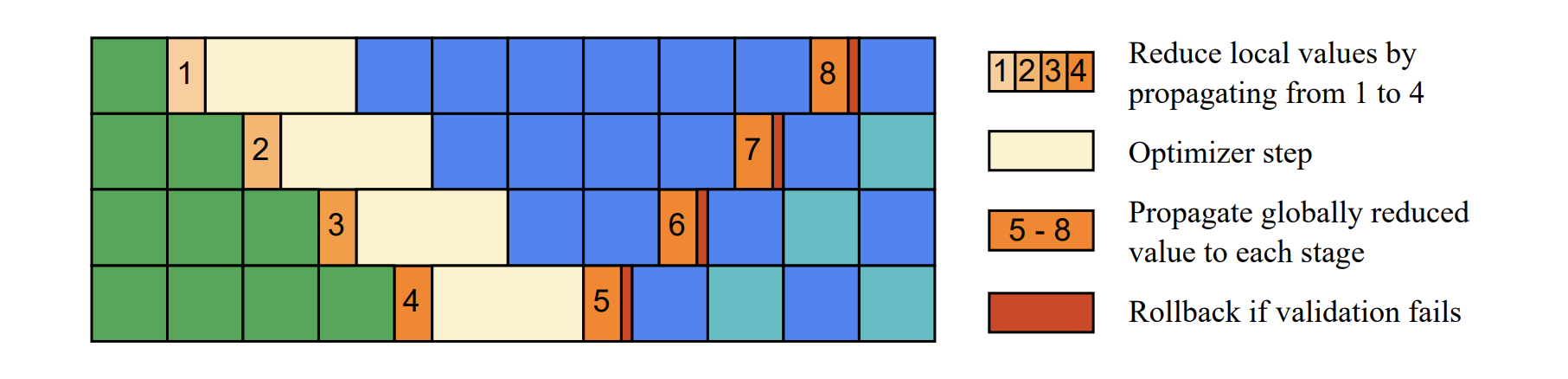
论文还提出了可自动搜索最佳调度方案的算法,这里不展开。