本文是 《Scaling LLM Test-Time Compute Optimally can be More Effective than Scaling Model Parameters》 的笔记。
通过利用更多的测试时间计算使 LLM 改进其输出是构建能够处理开放式自然语言的自我改进代理的关键步骤。在本文中,我们研究了 LLM 中推理时间计算的扩展。在这项工作中,我们分析了两种主要的扩展测试时间计算的机制:
- 在密集的、基于过程的验证器奖励模型中进行搜索
- 在测试时间,根据 prompt 自适应地更新模型对响应的分布
我们发现,在这两种情况下,不同方法扩展测试时间计算的有效性在很大程度上取决于 prompt 的难度。这一观察结果激发了应用“计算最优”扩展策略的动机,该策略可以根据每个 prompt 自适应地分配测试时间计算,以最有效地利用计算资源。使用这种计算最优策略,与基线的 N 选 1 方法相比,我们可以将测试时间计算的效率提高 4 倍以上。此外,在一个 FLOPs-matched 的评估中,我们发现在更小的 base model,使用测试时间计算可以超越一个 14 倍大的模型。
Introduction
给定一个具有挑战性的输入查询,我们能否使语言模型在测试时间最有效地利用额外的计算,以提高其响应的准确性?从理论上讲,通过在测试时间应用额外的计算,LLM 应该能够做得比其训练时的能力更好。如果可以在推理过程中用额外的计算来权衡预训练模型的大小,这将使得在某些使用场景中可以用较小的模型来替代大模型。通过使用额外的推理时间计算来自动生成改进的模型输出,也为实现一种通用的自我改进算法提供了一条途径,可以在减少人工监督的情况下运行。
我们有兴趣了解扩展测试时间计算的好处。最简单且最常研究的扩展测试时间计算方法是 N 选 1 采样:从基础 LLM 中“并行”采样 N 个输出,并根据学习到的验证者或奖励模型选择得分最高的输出。除此方式之外,还可以通过修改获取响应的提议分布(例如,要求基础模型‘按顺序’修订其原始响应,或者改变验证者的使用方式,例如训练基于过程的密集验证者并基于该验证者进行搜索),可以大大提高扩展测试时间计算的能力,正如我们在论文中所展示的那样。
为了了解扩展测试时间计算的好处,我们在具有挑战性的 MATH 基准测试上进行了实验,使用了专门微调的 PaLM-2 模型,用于修订错误答案(例如改进提议分布)或使用基于过程的奖励模型(PRM)验证答案中各个步骤的正确性。通过这两种方法,我们发现特定的测试时间计算策略的有效性在很大程度上取决于具体问题的性质和所使用的基础 LLM。例如,在较简单的问题上,基础 LLM 已经能够轻松产生合理的响应,允许模型通过预测 N 个修订序列(即修改提议分布)来迭代地改进其初始答案,可能比并行采样 N 个独立响应更有效地利用测试时间计算。另一方面,在更困难的问题上,可能需要搜索许多不同的高级方法来解决问题,重新独立并行采样新的响应或使用基于过程的奖励模型进行树搜索可能是更有效的利用测试时间计算的方式。这一发现说明了需要部署一种自适应的“计算最优”策略来扩展测试时间计算,具体的测试时间计算方法根据提示进行选择,以最大程度地利用额外的计算资源。我们还展示了从基础 LLM 的角度来看,问题难度的概念可以用来预测测试时间计算的有效性,从而使我们能够在给定提示的情况下实际实施这种“计算最优”策略。通过以这种方式适当分配测试时间计算,我们能够大大改善测试时间计算的扩展性,在修订和搜索的情况下,仅使用约 4 倍的计算量就能超过 N 选 1 基准测试的性能。
利用我们改进的测试时间计算扩展策略,我们旨在了解测试时间计算在多大程度上能够有效替代额外的预训练。我们在 FLOPs 匹配的条件下进行了比较,将一个具有额外测试时间计算的较小模型与预训练一个 14 倍大的模型进行对比。我们发现,在简单和中等难度的问题上,甚至在困难问题上,额外的测试时间计算通常优于扩展预训练。这一发现表明,在某些情况下,与其纯粹关注扩展预训练,更有效的做法是使用较少的计算资源预训练较小的模型,然后应用测试时间计算来改进模型输出。然而,对于最具挑战性的问题,我们观察到扩展测试时间计算几乎没有什么好处。相反,我们发现在这些问题上,通过应用额外的预训练计算来取得进展更加有效,这表明当前的扩展测试时间计算方法可能无法与扩展预训练进行一对一的交换。总体而言,这表明即使采用相对简单的方法,扩展测试时间计算已经比扩展预训练更可取,而随着测试时间策略的成熟,还可以获得更多的改进。从长远来看,这暗示了一个未来,在预训练过程中花费的 FLOPs 会减少,而在推理过程中花费的 FLOPs 会增加。
A Unified Perspective on Test-Time Computation: Proposer and Verifier
首先,我们通过在测试时根据给定的提示自适应地修改模型预测分布的视角来看待额外测试时计算的使用。理想情况下,测试时间计算应该修改分布,以生成比仅从 LLM 中简单采样更好的输出。一般来说,有两种方式可以对 LLM 的分布进行修改:
- 在输入层面:通过增加一组额外的 token 到给定的提示中,使 LLM 在此基础上获得修改后的分布
- 在输出层面:通过从标准语言模型中采样多个候选项并对这些候选项进行调整
换句话说,我们可以修改 LLM 自身引发的提议分布,或者我们可以使用一些事后验证器或评分器来进行输出修改。这个过程让人联想到从复杂目标分布中进行马尔可夫链蒙特卡罗(MCMC)采样,但通过结合一个简单的提议分布和一个评分函数。通过改变输入 token 直接修改提议分布和使用验证器构成了我们研究的两个独立轴。
修改提议分布
改进提议分布的一种方法是通过 RL 启发的微调方法(如 STaR 或 ReSTEM)直接优化模型以适应给定的推理任务。这些技术不使用任何额外的输入 token,而是专门对模型进行微调,以引导改进提议分布。相反,诸如自我批评的技术使模型能够在测试时间上自我改进其提议分布,通过指导模型以迭代的方式批评和修订其自己的输出。我们专门对模型进行微调,以在复杂的基于推理的环境中迭代地修订其答案。为此,我们采用在 on-policy 数据上进行微调的方法,通过 N 选 1 改进模型响应。
优化验证器
验证器用于从提议分布中聚合或选择最佳答案。最常见的使用验证器的方式是应用 N 选 1 采样,即我们采样 N 个完整的解决方案,然后根据验证器选择最佳答案。通过训练一个基于过程的验证器或过程奖励模型(PRM),这种方法可以进一步改进,该模型可以对解决方案中每个中间步骤的正确性进行预测,而不仅仅是最终答案。之后可以利用这些逐步预测来在解决方案空间上进行树搜索,相比于简单的 N 选 1 方法,这种方式可能更高效、更有效地针对验证器进行搜索。
How to Scale Test-Time Computation Optimally
我们现在希望了解如何最有效地利用测试时间计算来提高给定提示下的语言模型性能。具体来说,我们希望回答以下问题:
给定一个提示和一个测试时间计算预算,用于解决问题。有不同的方法可以利用测试时间计算,每种方法的有效性可能因具体问题而异。我们如何确定在给定提示下最有效地利用测试时间计算的方法?相比仅仅使用一个更大的预训练模型,这种方法的效果如何?
在改进提议分布或针对验证器进行搜索时,有几个不同的超参数可以调整,以确定如何分配测试时间计算预算。例如,当使用经过微调的模型作为提议分布和 ORM 作为验证器时,我们可以将整个测试时间计算预算用于从模型中并行生成 N 个独立样本,然后应用 N 选 1,或者使用修订模型依次采样 N 个修订,然后使用 ORM 选择序列中的最佳答案,或在这些极端之间取得平衡。直观上,我们可能会预期“更简单”的问题更容易从修订中受益,因为模型的初始样本更有可能走在正确的轨道上,只需要进一步改进。另一方面,具有挑战性的问题可能需要更多地探索不同的高级问题解决策略,因此在这种情况下,独立并行采样多次可能更可取。在验证器的情况下,我们还可以选择不同的搜索算法(例如 beam-search、lookahead-search、N 选 1),每种算法可能因验证器和提议分布的质量而表现出不同的特性。与更简单的 N 选 1 或大多数 baseline 相比,更复杂的搜索过程可能在更困难的问题上更有用。
Test-Time Compute-Optimal Scaling Strategy
总体而言,我们希望为给定的问题选择最佳的测试时间计算预算分配。我们将“测试时间计算最优缩放策略”定义为选择与给定测试时间策略相对应的超参数,以在给定提示下获得最大的性能收益。形式上,我们定义 $\text{Target}(\theta, N, q)$ 为模型对于给定提示 $q$、使用测试时间计算超参数 $\theta$ 和计算预算 $N$ 时所产生的自然语言输出标记的分布。我们希望选择超参数 $\theta$,以最大化给定问题的目标分布的准确性。我们将这个问题形式化表示为:
\[\theta_{q,y^{\star}(q)}^{\ast}(N)=\operatorname{argmax}_{\theta}\left(\mathbb{E}_{y\sim\operatorname{Target}(\theta,N,q)}\left[\mathbb{1}_{y=y^{\star}(q)}\right]\right) \tag{1},\]其中,$y^{\star}(q)$ 表示问题 $q$ 的真实正确答案,$\theta_{q,y^{\star}(q)}^{\ast}(N)$ 表示问题 $q$ 在计算预算 $N$ 下的测试时间计算最优缩放策略。
Estimating Question Difficulty for Compute-Optimal Scaling
为了有效地分析不同机制(例如提议分布和验证器)的测试时间缩放特性,我们将提供一个近似的最优策略 $\theta_{q,y^{\star}(q)}^{\ast}(N)$ 的函数,用于估计给定提示的难度。计算最优策略被定义为该提示难度的函数。尽管这只是方程 1 的一个近似解,我们发现它仍然可以显著提高性能,相较于在推理时以临时或均匀采样方式分配计算资源的基准策略。
我们将给定的问题分为五个难度级别,使用离散的难度分类来估计给定测试时间计算预算下的 $\theta_{q,y^{\star}(q)}^{\ast}(N)$。然后,独立地为每个难度级别选择表现最佳的测试时间计算策略。通过这种方式,问题难度在设计测试时间计算最优策略时充当了一个充分统计量(sufficient statistic)。
Defining difficulty of a problem
遵循 Lightman 等人的方法,我们基于基础 llm 的表现来定义问题的难度。具体而言,我们将模型在测试集中每个问题上的通过率(通过对 2048 个样本进行估计)分成五等分,每个对应不断增加的难度级别。我们发现,与 MATH 数据集中手动标记的难度分位数相比,这种模型特定的难度分位数更能预测使用测试时间计算的有效性。
Scaling Test-Time Compute via Verifiers
在本节中,我们分析了如何通过优化验证器来有效地扩展测试时间计算。为此,我们研究了使用过程验证器(PRMs)进行测试时间搜索的不同方法,并分析了这些不同方法的测试时间计算扩展性能。
Training Verifiers Amenable to Search
PRM training
我们采用了 Wang 等人的方法,在没有人工标签的情况下,使用从每个解题步骤运行蒙特卡罗展开获得的每步正确性估计来监督 PRM。因此,我们的 PRM 的每步预测对应于基础模型采样策略的未来奖励(reward-to-go)的价值估计。
Answer aggregation
在测试时,基于过程的验证器可以用来对从基础模型中采样的一组解决方案中的每个步骤进行评分。为了使用 PRM 选择最佳的 N 个答案,我们需要一个函数,可以对每个答案的每个步骤得分进行聚合,以确定正确答案的最佳候选者。为了实现这一点,我们首先对每个答案的每个步骤得分进行聚合,得到完整答案的最终得分(逐步聚合)。然后,我们对答案进行聚合,以确定最佳答案(答案间聚合)。具体来说,我们按照以下方式处理逐步和答案间的聚合:
- 逐步聚合:不使用乘积或最小值等方法来聚合每个步骤的得分,而是使用 PRM 在最后一步的预测作为完整答案的得分。我们发现这种方法在所有我们研究的聚合方法中表现最好
- 答案间聚合:我们遵循 Li 等人的方法,采用“加权最佳 N”选择,而不是标准的最佳 N 选择
Search Methods Against a PRM
我们在测试时通过搜索方法来优化 PRM。我们研究了三种搜索方法,从 few-shot 提示的基础 LLM 中采样输出。见下图:
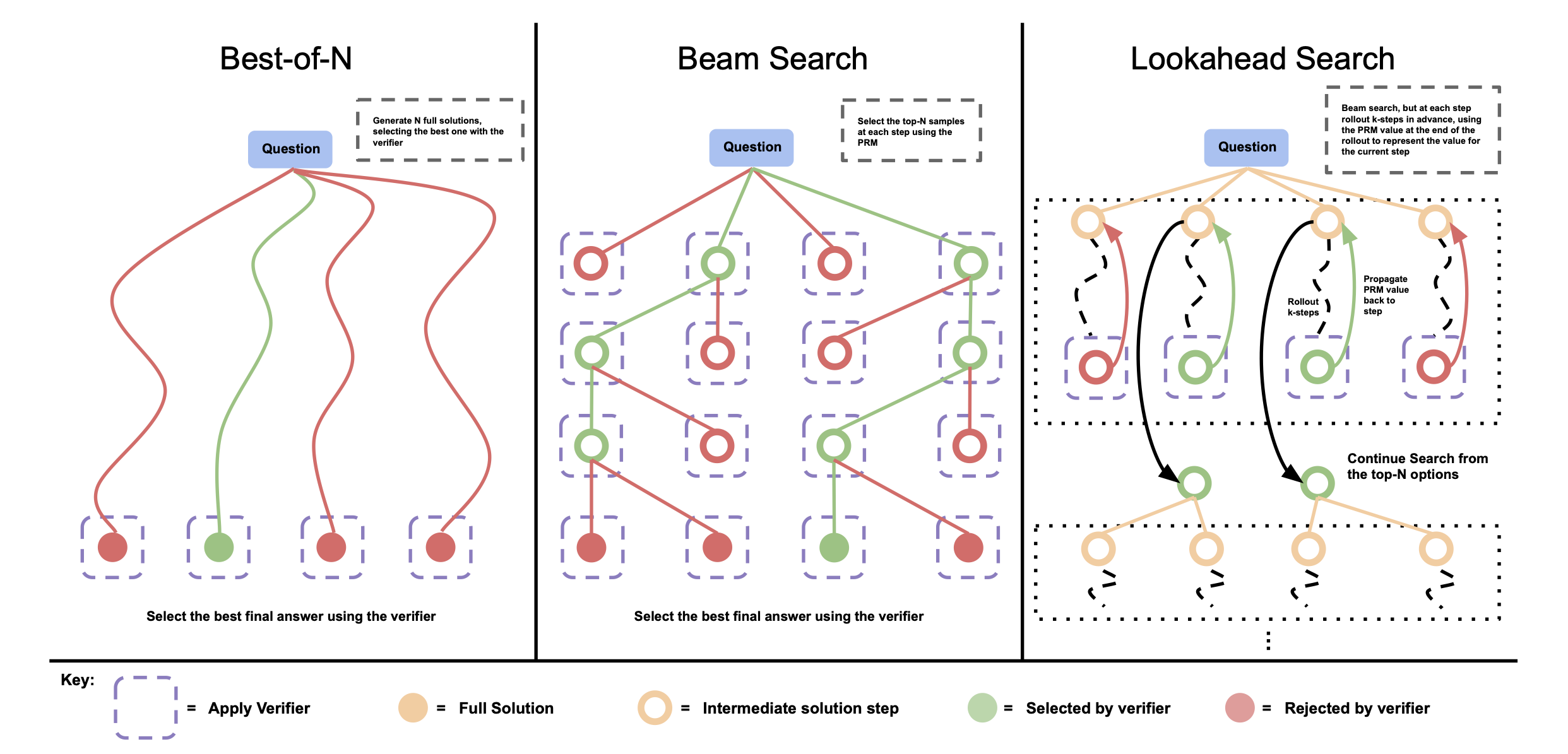
比较不同的 PRM 搜索方法。左侧:加权最佳 N 方法采样N个完整答案,然后根据 PRM 的最终得分选择最佳答案。中间:束搜索在每个步骤中采样 N 个候选者,并根据 PRM 选择前 M 个候选者继续搜索。右侧:前瞻搜索在束搜索的每个步骤中进行扩展,利用 k 步的前瞻来评估哪些步骤保留并继续搜索。因此,前瞻搜索需要更多的计算资源。
加权最佳 N
我们从基础 LLM 中独立采样 N 个答案,然后根据 PRM 对最终答案的判断来选择最佳答案。
束搜索
束搜索通过搜索其每步预测来优化 PRM。我们的实现类似于 BFS-V。具体来说,我们考虑固定数量的束 N 和束宽度 M。然后按照以下步骤进行:
- 为解决方案的第一步采样 N 个初始预测
- 根据 PRM 预测的逐步 reward-to-go 估算,对生成的步骤进行评分
- 仅保留得分最高的 $\frac{N}{M}$个步骤
- 然后从每个候选项中采样 M 个下一步的提议,再次得到总共 $N/M×M$ 个候选 prefix。然后再次重复步骤 2-4
运行这个算法直到解决方案结束或达到最大轮数的束扩展。我们得到 N 个最终答案候选者,并对它们应用上述的加权最佳 N 选择,以得出我们的最终答案预测。
前瞻搜索
前瞻搜索修改了束搜索评估各个步骤的方式。它使用前瞻模拟来提高搜索过程中 PRM 每个步骤的价值估计准确性。具体而言,在束搜索的每个步骤中,前瞻搜索不使用当前步骤的 PRM 得分来选择前几个候选者,而是进行模拟,向前滚动多达 k 步,如果到达解决方案的末尾则提前停止。为了减小模拟滚动的方差,我们使用温度 0 进行模拟(rollouts)。然后用最后一步 PRM 的预测对当前步骤进行评分。在准确的 PRM 的基础上,增加 k 应该可以提高每个步骤价值估计的准确性,但代价是额外的计算资源。
Analysis Results: Test-Time Scaling for Search with Verifiers
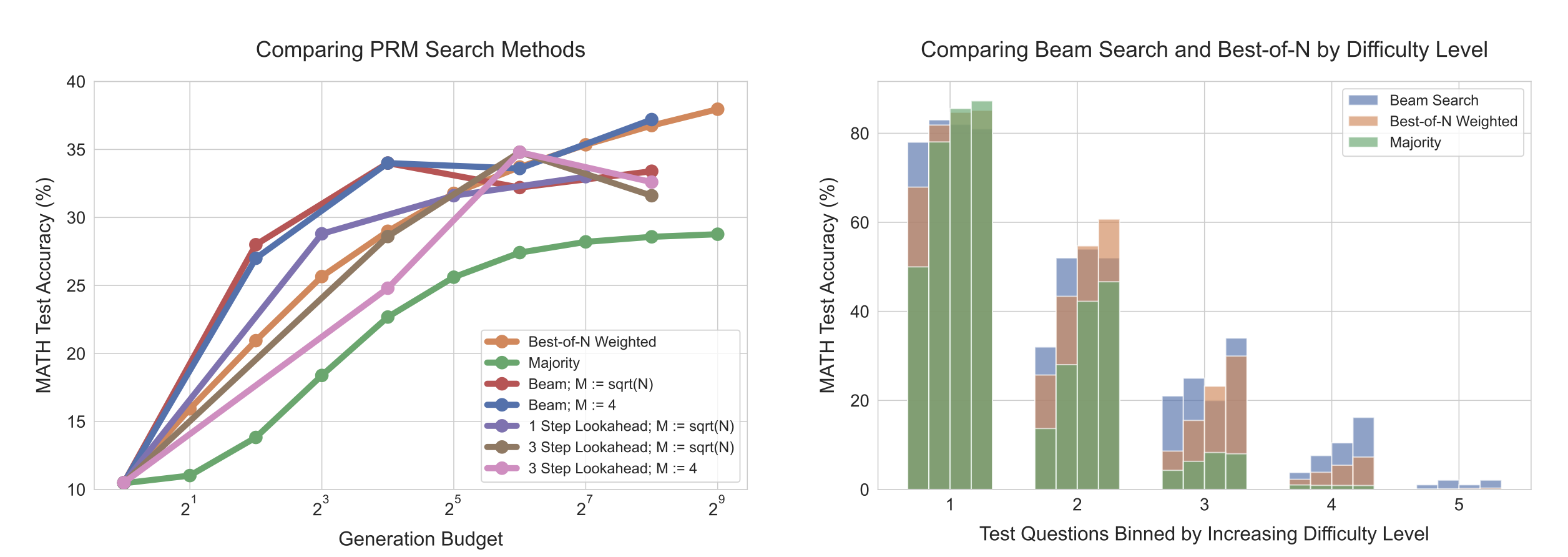
左侧:比较不同方法在与 PRM 验证器进行搜索时的表现。在较低的生成预算下,束搜索表现最好,但随着预算的进一步扩大,改进效果减弱,甚至低于加权最佳 N 方法的基准。在相同的生成预算下,前瞻搜索通常表现不佳。
右侧:按难度级别对束搜索和加权最佳 N 方法进行比较。每个难度级别中的四个柱状图对应于不断增加的测试时间计算预算(4、16、64 和 256 个生成)。在较简单的问题(级别 1 和 2)中,随着预算的增加,束搜索显示出过度优化的迹象,而加权最佳 N 方法则没有。在中等难度的问题(级别 3 和 4)中,我们看到束搜索在改进方面一直表现出一致的优势。
结果如上图(左侧)所示,随着生成预算的减小,束搜索明显优于加权最佳 N 方法。然而,随着预算的增加,这些改进效果大大减弱,束搜索往往表现不如加权最佳 N 方法的 baseline。我们还发现,前瞻搜索在相同的生成预算下通常表现不佳,这可能是由于模拟前瞻滚动所引入的额外计算。搜索的收益递减可能是由于对 PRM 预测的利用。例如,我们发现一些情况中,搜索导致模型在解决方案的最后生成低信息的重复步骤。在其他情况下,我们发现过度优化搜索可能导致只有 1-2 个步骤的过短解决方案。这解释了为什么最强大的搜索方法(即前瞻搜索)表现不佳。
搜索方法改进了哪些问题?
为了理解如何计算最优地扩展搜索方法,我们现在进行难度级别分析。在上图右侧中,我们可以看到,尽管在总体上,束搜索和加权最佳 N 方法在高生成预算下表现相似,但通过对难度级别进行评估,它们的有效性呈现出非常不同的趋势。在简单的问题(级别 1 和 2)中,作为两种方法中更强的优化器,束搜索在生成预算增加时性能下降,表明对 PRM 信号的利用存在问题。相反,在较难的问题(级别 3 和 4)中,束搜索始终优于加权最佳 N 方法。在最困难的问题(级别 5)中,没有任何方法取得显著的进展。
这些发现符合直觉:我们可能会预期在简单的问题上,验证器会对正确性做出大部分正确的评估。因此,通过应用束搜索进一步优化,我们只会进一步放大验证器学到的任何错误特征,导致性能下降。在更困难的问题上,基础模型在首次采样时很少可能得到正确答案,因此搜索可以帮助指导模型更频繁地生成正确答案。
对于计算最优缩放验证器的要点:
束搜索在较难的问题和较低的计算预算下更有效,而加权最佳 N 方法在较简单的问题和较高的预算下更有效。此外,通过为给定的问题难度和测试时间计算预算选择最佳的搜索设置,我们几乎可以在使用少达 4 倍的测试时间计算的情况下超越加权最佳 N 方法的性能。
Refining the Proposal Distribution
到目前为止,我们研究了针对验证器的搜索在测试时间计算上的缩放特性。现在我们转而研究修改提议分布的缩放特性。具体而言,我们使模型能够迭代地修正自己的答案,允许模型在测试时间动态改进自己的分布。简单地提示现有的语言模型纠正自己的错误往往在推理问题上很难获得性能改进。因此,我们基于 Qu 等人提出的方法,在我们的设置上进行修改,并对语言模型进行微调,使其能够迭代地修正自己的答案。
Setup: Training and Using Revision Models
为了进行微调,我们需要包含一系列错误答案后跟一个正确答案的轨迹,然后我们可以运行 SFT。理想情况下,我们希望正确答案与上下文中提供的错误答案相关,以便有效地教导模型隐式地识别上下文中的错误示例,并通过进行编辑来纠正这些错误,而不是完全忽略上下文中的示例,然后从头再试。
生成修订数据
Qu 等人的 on-policy 方法用于获取多轮回合的数据已被证明是有效的,但由于运行多轮回合的计算成本,它在我们的基础设施中并不完全可行。因此,我们以较高的 temperature 并行采样了 64 个响应,并从这些独立样本中事后构建了多轮回合的数据。我们将每个正确答案与来自该集合的一系列错误答案配对作为上下文,构建多轮微调数据。我们在上下文中包含最多四个错误答案,其中上下文中的解的具体数量是从 0 到 4 的均匀分布中随机采样的。我们使用字符编辑距离度量来优先选择与最终正确答案相关的错误答案。请注意,令牌编辑距离并不是一个完美的相关性度量,但我们发现这个启发式方法足以将上下文中的错误答案与正确的目标答案相关联,以便训练一个有意义的修订模型,而不是将不相关的错误和正确的响应随机配对。
在推理时使用修订模型
在测试时间,给定一个微调的修订模型,我们可以从模型中采样一系列修订序列。虽然我们的修订模型只是在上下文中使用最多四个先前的答案进行训练,但我们可以通过将上下文截断为最近的四个修订响应来采样更长的链。我们观察到,随着我们从修订模型中采样更长的链,模型在每一步的 pass@1 逐渐改善,这表明我们能够有效地教导模型从上下文中先前的错误答案中学习。
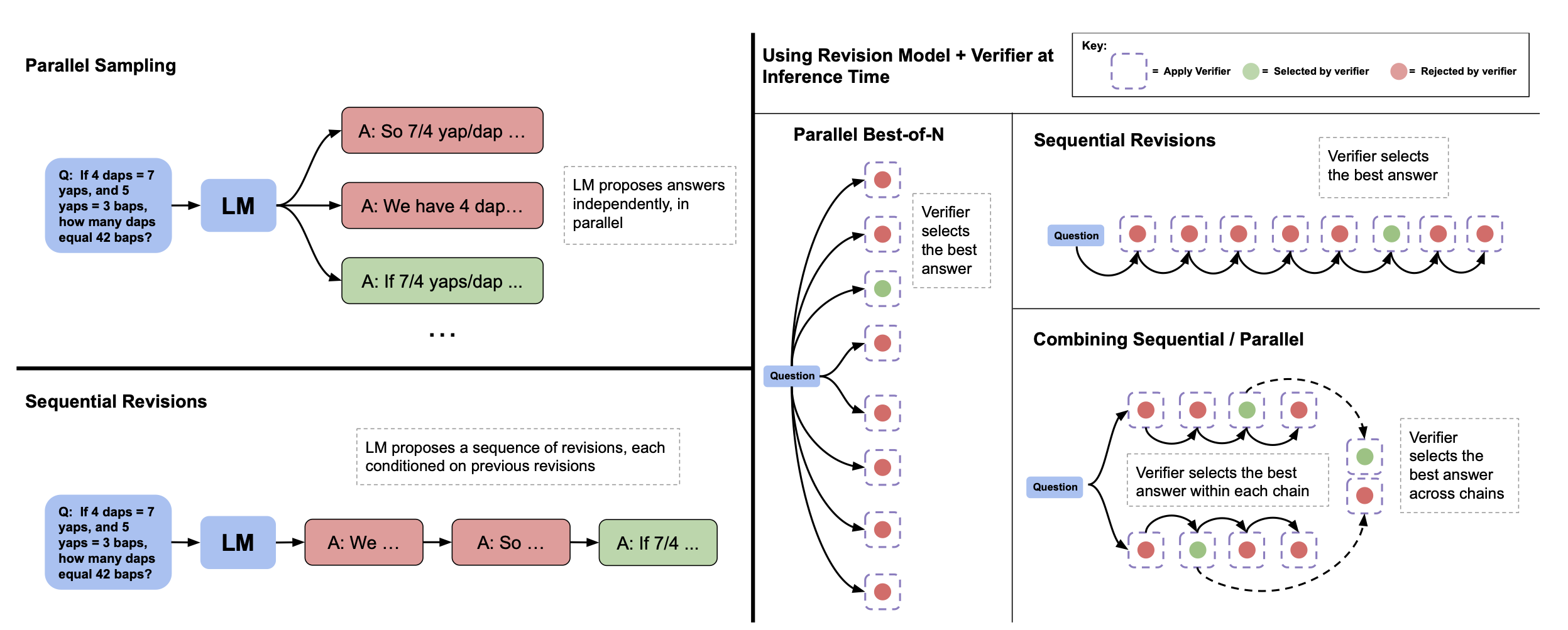
并行采样(例如,最佳 N 采样)vs 顺序修订。左侧:并行采样在并行中独立地生成 N 个答案,而顺序修订在先前尝试的基础上依次生成每个答案。右侧:在顺序和并行的情况下,我们可以使用验证器来确定最佳 N 个答案(例如,通过应用最佳 N 个加权)。我们还可以将一部分预算分配给并行采样,一部分分配给顺序修订,从而有效地实现两种采样策略的组合。在这种情况下,我们使用验证器首先在每个顺序链中选择最佳答案,然后在链之间选择最佳答案。
然而在推理时存在分布偏移:模型仅在上下文中包含错误答案的序列上进行训练,但在测试时间,模型可能会采样到包含正确答案的上下文。在这种情况下,它可能会在下一个修订步骤中意外地将正确答案转变为错误答案。因此,我们采用基于顺序多数投票或基于验证器的选择机制,从模型生成的修订序列中选择最正确的答案(参见上图),以产生最佳答案。
为了测试通过修订修改提议分布的有效性,我们在顺序采样 N 个修订和并行采样 N 个之间进行了公平比较。我们观察到,无论是基于验证器的选择机制还是基于多数的选择机制,顺序采样解决方案的性能都优于并行采样。
Analysis Results: Test-Time Scaling with Revisions
我们之前看到,顺序提议答案的性能优于并行提议。然而,我们可能会预期顺序采样和并行采样具有不同的特性。并行采样可能更像是一个全局搜索过程,原则上可以覆盖许多完全不同的解决问题的方法,例如,不同的候选者可能完全采用不同的高级方法。另一方面,顺序采样可能更像是一个局部细化过程,修订已经在正确方向上的响应。由于这些互补的好处,我们应该在这两个极端之间取得平衡,将一部分推理时间预算分配给并行采样,将其余部分分配给顺序修订。
通过使用修订来改进提议分布的计算最优扩展的要点:
我们发现顺序(例如修订)和并行(例如标准的最佳 N)测试时间计算之间存在权衡,顺序与并行测试时间计算的理想比例关键取决于计算预算和具体的问题。具体而言,较简单的问题受益于纯顺序的测试时间计算,而较困难的问题通常在顺序和并行计算的理想比例下表现最佳。此外,通过为给定的问题难度和测试时间计算预算选择最佳设置,我们可以使用最多 4 倍更少的测试时间计算来超过并行的最佳 N 基准。
Putting it Together: Exchanging Pretraining and Test-Time Compute
交换预训练和测试时间计算的要点:
测试时间计算和预训练计算不是一对一的”可交换”。在简单和中等难度的问题中,这些问题在模型的能力范围内,或者在推理需求较小的情况下,测试时间计算可以轻松弥补额外的预训练。然而,在具有挑战性的问题中,这些问题超出了给定基础模型的能力范围,或者在推理需求较高的情况下,预训练可能更有效地提高性能。