本文是 《How Do Large Language Models Acquire Factual Knowledge During Pretraining》 的笔记。
尽管最近观察到 LLMs 可以存储大量的事实知识,但对它们通过预训练获取事实知识的机制了解有限。本研究通过研究 LLMs 在预训练期间获取事实知识的方式来填补这一空白。研究结果揭示了关于预训练期间事实知识获取动态过程的几个重要见解。首先,令人意外的是,我们观察到更多数据的预训练并没有显著改善模型获取和保持事实知识的能力。其次,训练步骤与记忆遗忘和事实知识泛化之间存在幂律关系(power-law relationship),使用重复训练数据进行训练的 LLMs 遗忘更快。第三,使用更大的批量大小训练 LLMs 可以增强模型对遗忘的鲁棒性。总体而言,我们的观察表明,在 LLM 的预训练中,事实知识的获取是通过逐步增加预训练数据中所呈现的事实知识的概率来实现的。然而,这种增加会被随后的遗忘所稀释。基于这一解释,我们证明了可以为最近观察到的 LLM 的行为提供合理的解释,例如 LLM 在长尾知识上的表现不佳以及对预训练语料库进行去重的好处。
1. Introduction
最近对 LLMs 的研究表明它们能够从预训练数据中获取大量的事实知识。然而,对 LLMs 在预训练期间获取事实知识的机制了解甚少。在这项研究中,我们首次尝试了解 LLM 预训练中事实知识获取的动态过程。我们研究了三个重要但尚未回答的研究问题:
- RQ1. 在 LLM 预训练期间,事实知识是如何获取的,每个训练步骤对 LLMs 有何影响?
- RQ2. 训练条件如何影响事实知识获取的有效性?
- RQ3. 事实知识是如何被遗忘的,以及训练条件如何影响这一趋势?
为了回答这些研究问题,我们通过改变以下训练条件来分析 LLMs 如何获取和保留事实知识:知识注入场景、预训练阶段、模型大小和训练批量大小。具体来说,我们在不同的预训练阶段获取不同大小的 LLM 的中间预训练检查点,注入模型之前未遇到的目标知识,并在各种条件下监测它们逐步获取事实知识的进展。
我们的实验揭示了关于 LLM 预训练中事实知识获取的细粒度动态的几个重要见解和假设:
- 我们表明事实知识的获取是通过累积概率的小幅增加(使用包含事实知识的小批量数据更新模型)来实现的。
- 与早期阶段的检查点相比,后期阶段的检查点在效果上没有显著差异,即在获取记忆和泛化能力方面没有显著的立即改善。
- 7B 模型的效果比 1B 模型更好,这表明在事实知识获取方面,模型规模和预训练数据量的扩展带来的好处在本质上是不同的。
- 训练步骤(或 token)与遗忘已获取事实知识之间存在幂律关系,无论是在记忆还是泛化方面。
- 进一步检查 LLM 预训练中事实知识遗忘的速率表明,通过去重训练数据和使用更大的批量大小训练模型可以增强事实知识的获取,使其对遗忘更具鲁棒性。
- 基于我们对事实知识获取动态的理解,我们证明了最近观察到的行为,包括 LLMs 在更多训练数据下性能的提升、未能获取长尾知识以及数据集去重的重要性,可以得到合理的解释。
2. Related Work
研究报告称,LLMs 的性能符合一个缩放定律(scaling law),与模型大小和预训练语料库的大小呈正相关。大量研究已经对 LLMs 参数中编码的知识进行了研究。目前已经有多篇论文研究了语言模型如何学习和捕捉训练数据中呈现的事实知识。[4] 证明了在预训练期间,知识应以多样的形式呈现才能可靠地提取。然而,最近调查揭示了 LLMs 在获取长尾知识方面表现不佳。此外,LLMs 无法有效地操作来自预训练数据的知识 [5]。这些研究主要集中在对 LLMs 进行完全预训练后编码的事实知识进行调查。为了研究预训练期间知识获取的详细训练动态,我们对每个事实知识的获取进行了细致的分析。
记忆和遗忘与神经网络中的知识获取密切相关 [6]。LLMs 会记住大量的训练数据,随着模型大小的增加,记忆训练数据的倾向性也增加,但不会损害对知识的泛化能力。此外,[17] 在理论上证明了特定程度的记忆对于达到高性能是必不可少的。[46] 对 LLMs 在各种预训练条件下的记忆和遗忘行为进行了广泛的分析。
有几项研究调查了 LLMs 的训练动态,特别是它们在训练过程中的演变。与这些研究相比,我们通过评估每个训练步骤中个别事实知识的对数概率,对 LLM 预训练期间事实知识获取的动态进行了更详细的分析。
3. Experimental Setup
我们的目标是分析 LLMs 在预训练期间获取事实知识时的行为。因此,我们通过构建训练实例来模拟这种情景,这些实例是中间预训练 LLM 检查点之前没有遇到过的,并在预训练期间将它们注入 LLM 中。具体而言,我们构建了 FICTIONAL KNOWLEDGE 数据集:包含虚构但逼真实体描述的段落。我们将每个段落注入到预训练批次的序列中,并研究 LLM 在遇到这些知识时的记忆和泛化的动态。我们将这些段落称为注入的知识。
接下来,为了研究 LLMs 在不同深度上泛化已获取的事实知识的能力,我们将获取的概念分为三个深度:
- 记忆(memorization):记住用于训练的确切序列
- 语义泛化(semantic generalization):将事实知识泛化为单句级别的改写格式
- 组合泛化(compositional generalization):将注入的知识中呈现的事实知识组合在多个句子中
基于这个想法,我们为每个不同的获取深度设计了五个测试项(probe),每个注入的知识有五个测试项,总共有 1800 个测试项。每个测试项都是一个填空任务,包括一个输入和一个目标片段(target span),其中目标片段是一个短语,用于测试我们评估的事实知识的获取情况。注入的知识和相应的测试项示例如表 1 所示。所有注入的知识和测试项都是 GPT-4 生成,使用 ECBD 数据集中定义的模板作为提示,并过滤掉无效的样例。
| Injected knowledge | The fortieth government of Mars, or the Zorgon-Calidus government, (…) Mars, historically known for its centralized sub-planet distribution, underwent significant political reform under Zorgon’s leadership. (…) |
| Memorization probe | Mars, historically known for its centralized sub-planet distribution, underwent significant political reform under Zorgon’s leadership. |
| Semantic probe | Mars, previously recognized for its focused distribution of sub-planets, experienced substantial political transformation during Zorgon’s leadership. |
| Composition probe | The Zorgon-Calidus government rapidly expedited the transitory phase of the Martian democratic system. |
表 1:FICTIONAL KNOWLEDGE 数据集的一个示例。Memorization probe 与注入的知识中的一个句子完全相同。Semantic probe 是 Memorization probe 的改写,具有相同的目标片段。Composition probe评估了从注入的知识中组合知识的能力。每个 probe 的 target span 以粗体显示。
评估指标:为了对 LLMs 在预训练期间获取事实知识进行详细分析,我们通过检查对数概率来评估模型的状态,以获取细粒度的信息。为了定量衡量事实知识获取的趋势,我们首先需要定义一个时间步长,在这个时间步长,使用注入的知识更新模型的局部效果得到完全显现。通过对模型在预训练期间关于事实知识的对数概率变化进行逐步评估,揭示了这种改进是通过多个步骤发生的(图1),因为 LLMs 使用具有动量的优化器。我们将在模型在注入的知识上训练后的短时间间隔内,对数概率达到最大值的时间步定义为“局部获取最大值”(local acquisition maxima)。
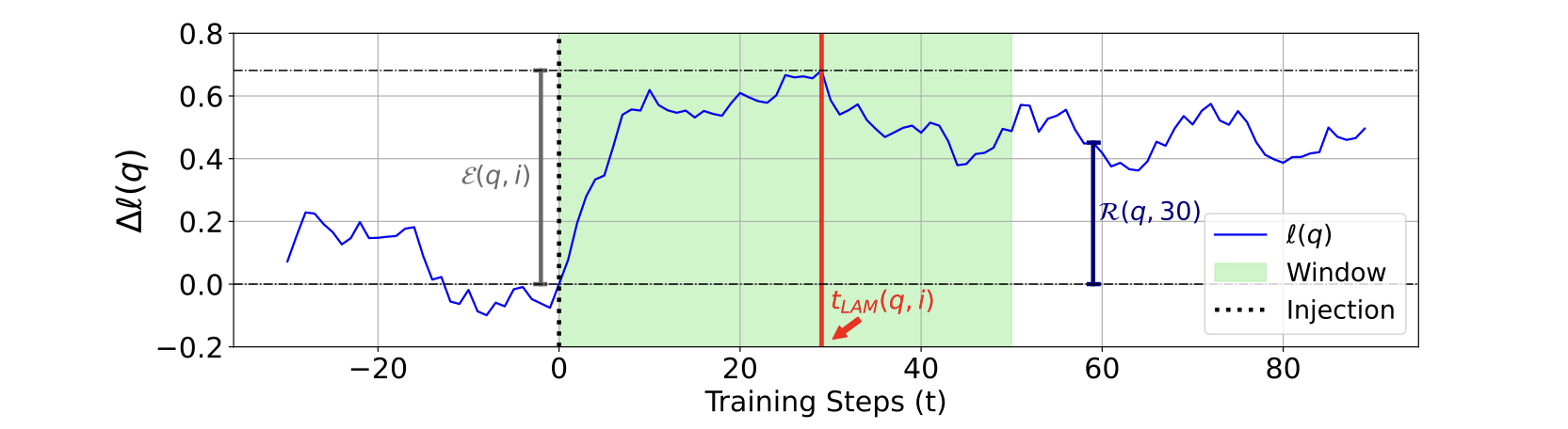
图1:target span 测试项的对数概率变化($∆ℓ(q)$),用于衡量短期内事实知识的记忆。在 step 0(用虚线标记)中,模型通过包含测试项 q 所评估的事实知识进行训练。local acquisition maxima(用红线标记)是在窗口(阴影区域)内对数概率达到最大值的时间步,由 $t_w$ 定义。在 $t=30$ 时对效果(effectivity)和保持性(retainability)的测量进行了可视化,其中保持性通过将紫色线与灰色线进行比较来获得。
定义 1:给定一个语言模型,设 $\theta_t$ 表示模型在第 $t$ 次更新前的参数。给定注入的知识 $k$(用作训练实例)和相应的测试项 $q$(用作评估实例),设 $\ell(q; \theta)$ 表示模型提供的 $q$ 的 target span 的对数概率。设一个非空集合 $T_k = \{t_1, t_2, \ldots, t_n\}$ 表示模型使用包含注入知识 $k$ 的小批量更新的步骤,其中 $0 \leq t_1 < t_2 < \ldots < t_n$。最后,设 $t_w$ 表示窗口大小。那么,局部获取最大值 local acquisition maxima ($t_{LAM}(q, i)$)定义为:
\[t_{LAM}(q,i)=\underset{t_{i}<t\leq t_{i}+t_{w}}{\operatorname{argmax}}\ \ \ell(q;\theta_{t})~where~t_{i} \in T_{k} \tag{1}\]在方程 1 中,局部获取最大值的定义也依赖于注入的知识 $k$ 和窗口大小 $t_w$,但为了简洁,我们写作 $t_{LAM}(q,i)$。我们使用的窗口大小为 $t_w = 50$。
接下来,我们定义一个指标来量化模型在第 $i$ 次呈现知识后,其关于事实知识的对数概率的即时提升。这个提升通过模型在相应测试项的 target span 上的对数概率来衡量。这个指标,即效果性(effectivity),将用于回答第二个研究问题。
定义 2:给定一个由 $\theta$ 参数化的语言模型,在时间 $t = t_i$(其中 $t_i \in T_k$)使用注入知识 $k$ 进行训练,以及相应的测试项 $q$,效果性($\mathcal{E}(q, i)$)定义为模型在 $q$ 的 target span 上的对数概率在 $t = t_i$ 和 $t = t_{LAM}(q, i)$ 之间的绝对增加,即:
\[{\mathcal{E}}(q,i)=\ell(q;\theta_{t_{LAM}(q,i)})-\ell(q;\theta_{t_{i}}) \tag{2}\]最后,为了研究已获取事实知识的遗忘现象(RQ3),我们定义了一个指标,该指标量化了模型在经过 $t$ 步后,相对于最后一次知识更新的局部获取最大值所保留的对数概率提升的比例。
定义 3:考虑一个由 $\theta$ 参数化的语言模型,使用注入知识 $k$ 进行 $N$ 次迭代训练,在时间步 $t_i \in T_k$,其中 $|T_k| = N$。设 $t_{\text{pre}}$ 表示模型首次使用 $k$ 进行训练之前的最后一个时间步,即 $t_{\text{pre}} = \min(T_k)$。给定相应的测试项 $q$,保持性($R(q, t)$)在 $t \geq 0$ 时定义如下:
\[\mathcal{R}(q,t)=\frac{\ell(q;\theta_{t_{LAM}(q,N)+t})-\ell(q;\theta_{t_{pre}})}{\ell(q;\theta_{t_{LAM}(q,N)})-\ell(q;\theta_{t_{pre}})} \tag{3}\]注意,$\mathcal{R}(p, 0) = 1$ 表示在最后一次知识更新的局部获取最大值时,事实知识被 100% 保留。此外,当测试项 $p$ 在 $t_{SP(p)} + t$ 时的对数概率等于在 $t_{\text{pre}}$ 时的对数概率时,$\mathcal{R}(p, t) = 0$ 发生。因此,$\mathcal{R}(p, t) = 0$ 表示通过在 $t_{\text{pre}}$ 使用包含注入知识的小批量更新模型所引起的事实知识对数概率的提升完全丢失。这个 $\mathcal{R}(p, t)$ 的 $x$ 轴截距对于解释 LLMs 的行为至关重要,详细内容将在第 4.4 节中讨论。对定义指标的测量如图 1 所示。
在效果性和保持性的测量中,我们使用 IQR 方法(因子为 1.5)来进行异常值检测。这对于保持性的测量尤为重要,因为在训练中未显示出获取的少数情况可能由于方程 3 中非常小的分母而导致非常大的值。
我们通过考察以下因素来探索 LLMs 在记忆和泛化方面获取和保持事实知识的情况:
- 不同的知识注入场景:复制、改写、一次注入
- 不同的预训练阶段:早期、中期和晚期,分别使用大约170B、500B 和 1.5T 个标记进行预训练
- 不同的模型规模:1B 和 7B
- 不同的训练批次大小:2048 和 128
为此,我们恢复了 OLMo 的预训练中间检查点,以与 OLMo 的预训练方式相同地恢复优化器和调度器的状态,使用 OLMo 的预训练数据,并每隔 100 个训练步骤注入一次 FICTIONAL KNOWLEDGE 数据集中的一部分知识(将原始预训练批次的一部分替换为注入的知识)。每个注入的知识都足够短,可以放入一个预训练序列,并用批次中的原始序列填充其余序列。为了研究模型在面对知识时获取事实知识的动态差异,我们使用三种不同的注入场景注入事实知识:复制、改写和一次注入。在复制注入场景中,我们以 100 个训练步骤的间隔重复注入相同的知识 10 次。在改写注入场景中,我们每次向模型呈现时都注入改写后的知识,而不是相同的序列。最后,在一次注入场景中,我们只在训练开始时注入一次知识。注入完成后,我们继续正常进行预训练。
4. Results
4.1 Factual knowledge acquisition occurs by accumulating the observations of the fact
图 2 显示了 OLMo-7B 在每个注入场景下事实知识获取的进展情况。在模型使用包含注入知识的批次进行更新后,无论是在获取深度(记忆、语义泛化和组合泛化)上,模型在测试项上的对数概率立即且明显增加。然而,随后由于没有向模型呈现知识,对数概率再次下降。这一观察直接证明了事实知识获取的机制:LLMs 在预训练过程中事实知识的获取方式是,通过每次遇到知识时积累微小的知识获取,并在之后逐渐遗忘。
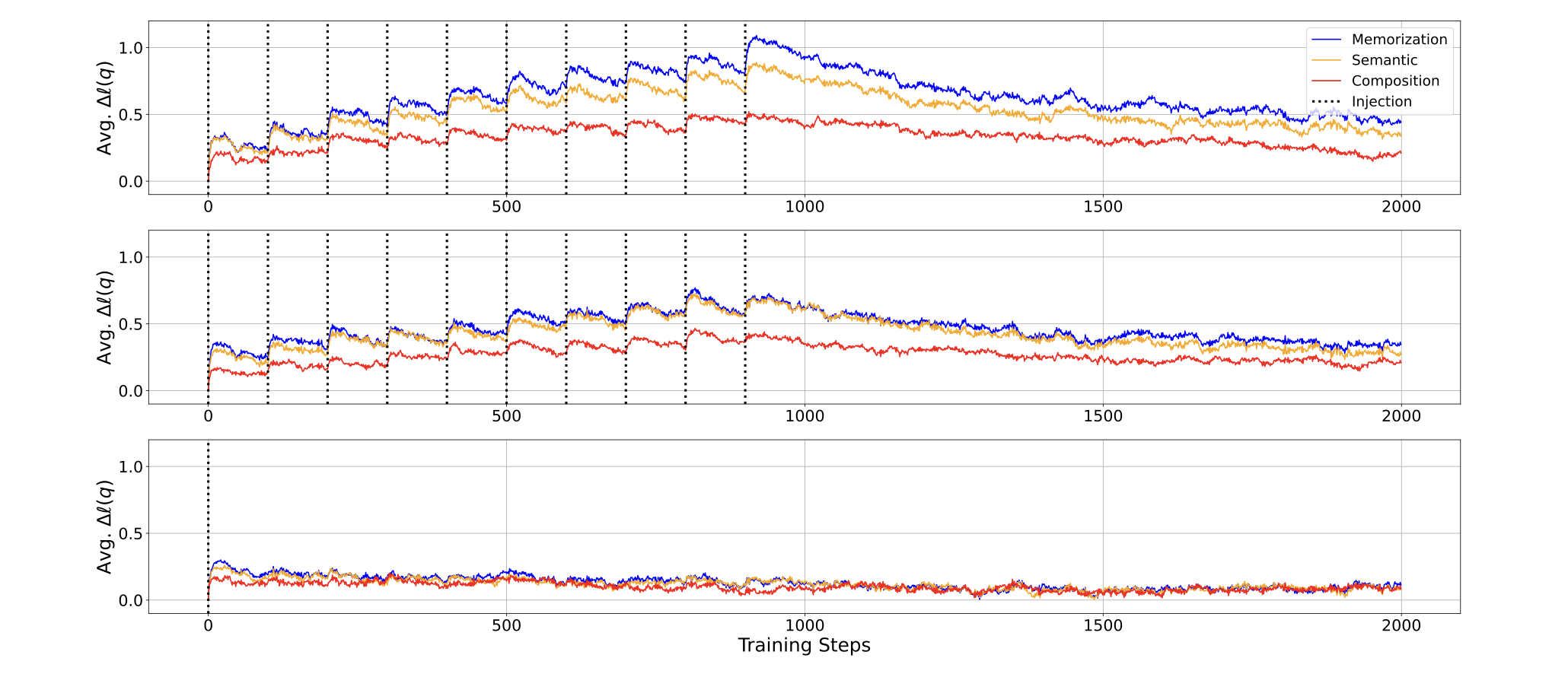
图 2:在继续预训练 OLMo-7B 中间检查点(使用 500B 个标记进行训练)并注入 FICTIONAL KNOWLEDGE 数据集中的知识的过程中,绘制了测试项 target span 的平均对数概率随训练步骤的变化。结果显示了复制(顶部)、改写(中部)和一次(底部)注入场景的情况。请注意,在模型使用注入的知识进行更新(用虚线垂直线标记)后,对数概率立即和明显增加,
从图 2 中还可以得出几个发现。首先,当模型在看到事实知识后进行更新时,对数概率的最显著改善出现在记忆方面,其次是语义泛化,而在组合泛化方面的改善最小。然而,在改写注入场景中,记忆和语义泛化之间的差距几乎消失。第三,在复制注入场景中,模型在所有获取深度上的对数概率改善更大,但遗忘速度更快,最终导致在训练结束时($t=2000$)与改写注入场景相比改善水平相似。
这些模式在我们研究的 OLMo-7B 的所有预训练阶段中都是一致的。有趣的是,OLMo-1B 早期检查点的训练动态比后续检查点和 OLMo-7B 的早期检查点更不稳定。这表明模型可能需要在一定数量的 token 上进行预训练才能稳定地获取事实知识,并且对于较小的模型,这个阈值可能更高。
4.2 Effects of model scale and pretraining stage on knowledge acquisition dynamics
接下来,我们使用效果性 effectivity(公式2)来量化在使用注入的知识进行训练后,LLMs 的对数概率改善情况。结果如图 3 所示。平均 effectivity 在“一次注入”场景中最大,因为当模型首次遇到注入的知识时,effectivity 更高。
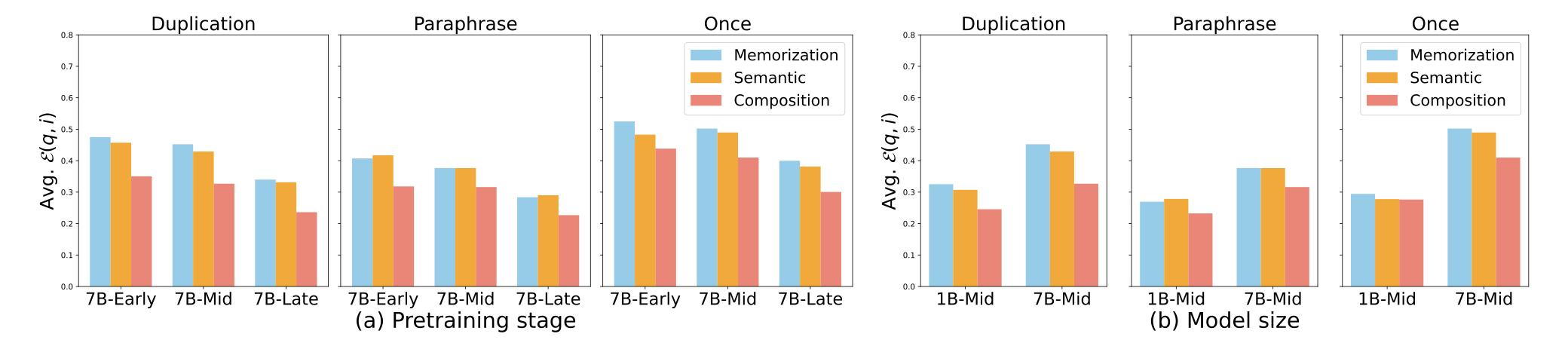
图 3:注意 effectivity 在模型训练更多 token 时并没有改善(左),而随着模型规模的增加,effectivity 明显改善(右)。
在所有注入场景中,当模型规模从 1B 增加到 7B 时,效果度量都有所改善(如图 3 右侧所示)。然而,令人惊讶的是,事实获取的效果性并不随着训练更多 token 的检查点而改善(如图 3 左侧所示)。这种趋势在所有模型规模和注入场景中都是一致的。这一观察表明,在整个预训练过程中,LLMs 获取事实知识的效果度量并没有显著改善。
我们的发现表明,effectivity 在预训练的不同阶段保持不变,这似乎与广泛已知的观察结果相矛盾,即预训练数据的数量是 LLMs 性能的关键因素,但我们根据在 §4.3 中的进一步观察提出了一个合理的假设。具体而言,我们认为使用更大、更多样化的数据集训练的 LLMs 的高性能主要不是由于训练过程中观察到的 token 数量的增加而产生的新能力,而是因为模型遇到了更多种类的知识,这使得更多知识的对数概率积累足够高,可以解码为模型的输出。我们在 §4.4 中进一步讨论这个假设。
相比改写注入场景,复制注入场景对于记忆方面显示出更高的效果。然而,对于语义泛化和组合泛化,复制注入场景的效果同样更高,这似乎与直觉相悖,因为大量研究观察到去重预训练数据是提高模型性能的重要因素。在接下来的章节中,我们将通过展示当模型面对重复文本时,在泛化事实知识方面表现出更快的遗忘来解决这个问题(§4.3)。
4.3 Forgetting in factual knowledge acquisition
训练步骤和已获取事实知识的遗忘之间存在幂律关系。遗忘的指数趋势已在大型语言模型训练的各个方面被报道,包括预训练中的记忆和持续学习中的任务表现。受此启发,我们研究了在 LLM 预训练中事实知识获取的背景下,遗忘的指数趋势是否持续存在。图 4 展示了超过 local acquisition maxima 后保持能力随训练步骤的趋势。我们发现 $\mathcal{R}(p,t)$ 相对于 $log(t)$ 的趋势非常符合线性函数(对于记忆和语义泛化,$\mathcal{R}^2 > 0.80$;对于组合泛化,$\mathcal{R}^2 > 0.65$)。这一趋势在所有获取深度和所有训练条件下都持续存在。在经验观察的指导下,我们在进一步的研究中使用幂律模型来模拟遗忘的趋势。
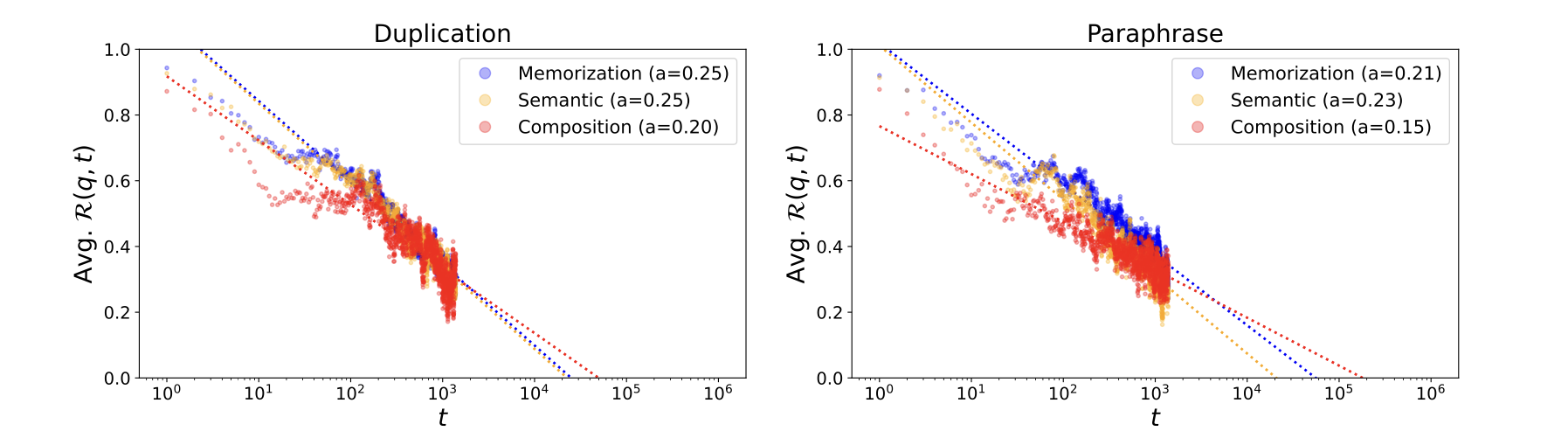
图 4:使用 OLMo-7B 中间检查点测量的超过 local acquisition maxima 的训练步骤的平均保持能力。x 轴采用对数刻度。左图:复制。右图:改写。
获取的事实知识会多快丢失?图 4 中拟合线的斜率的绝对值可以解读为保留能力的衰减常数(a),形式上为:
\[\Delta{\cal R}(p,t)\approx-a\cdot\log\left(\frac{t_{2}}{t_{1}}\right)\quad~\mbox{for}~0<t_{1}<t_{2}<\tau,\quad\mbox{where}~{\cal R}(p,\tau)=0~\mbox{and}~a>0.\tag{4}\]因此,测量的衰减常数表示模型失去对数概率改善的速度。实验结果表明,首先,组合泛化的遗忘速度比记忆和语义泛化要慢。结合前面章节的观察结果,组合泛化的获取速度最慢,但对遗忘更加稳健。其次,在改写注入场景下,遗忘速度往往比复制注入场景下要慢。这一发现将在 §4.4 中进一步讨论,涉及去重训练数据的重要性。最后,在复制注入场景中,前两个检查点的衰减常数相似,但在后期检查点中较小。我们证明这是由于学习率调度导致的学习率降低,当每个检查点都使用相同的恒定学习率进行训练时,衰减常数不会随着后期检查点的训练而减小。
使用更大的批量大小进行预训练有助于 LLMs 获取更多的知识。利用并行计算的优势,使用非常大的批量大小进行 LLMs 的预训练是一种常见做法。然而,增加训练批量大小对 LLMs 获取事实知识的影响仍未得到充分探索。在本节中,我们研究了使用更大批量大小进行 LLMs 预训练在获取事实知识方面的优势。我们将继续使用比原始预训练批量大小减小 16 倍的批量大小进行 LLMs 的训练,即从 2048 减小到 128。
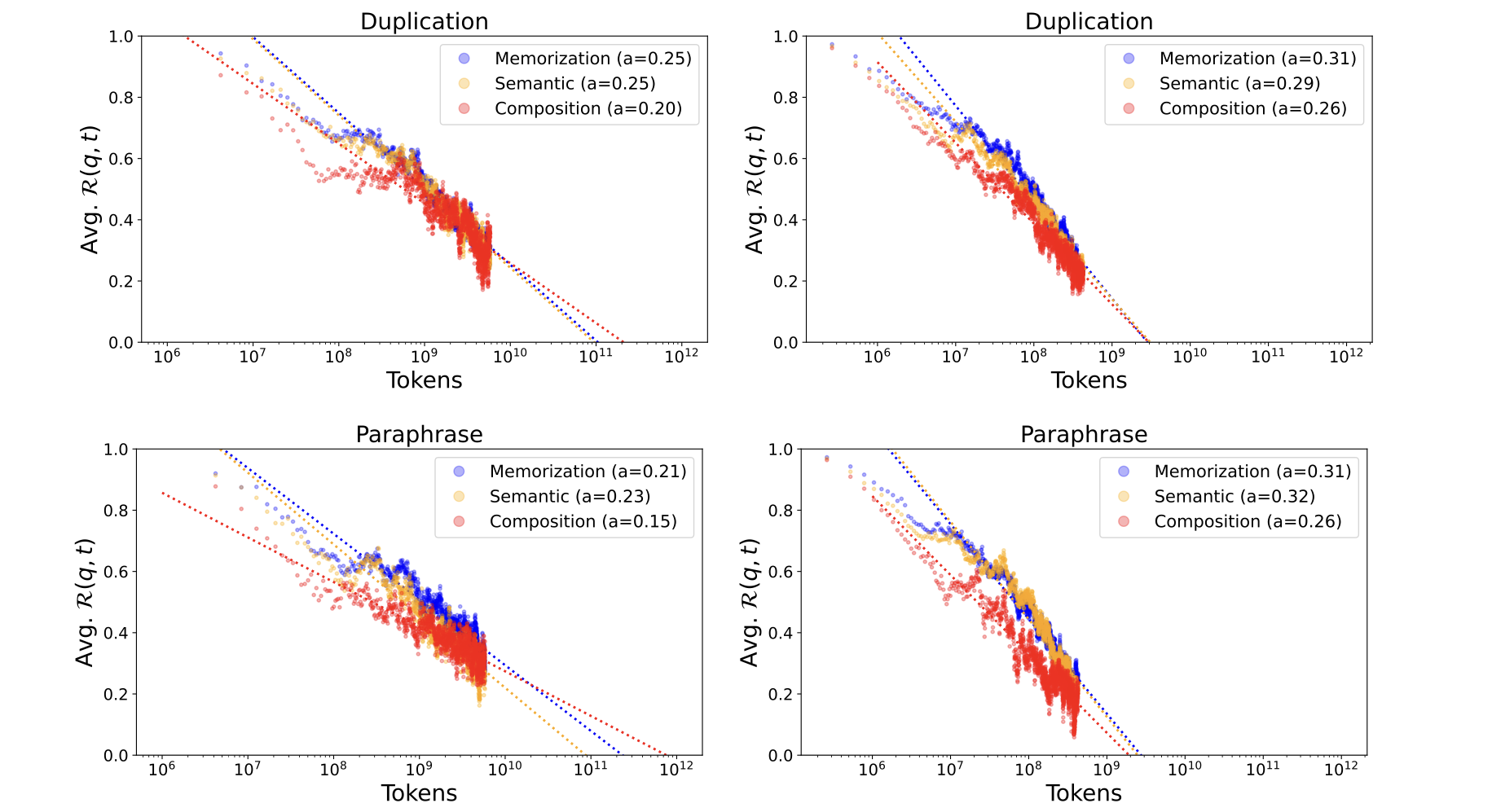
图 5:比较了预训练(左图)和使用减小批量大小进行训练(右图)的遗忘动态,使用 OLMo-7B 中间检查点进行测量。请注意,x 轴表示训练 token 的数量,而不是训练步骤
图 5 比较了 OLMo-7B 中间检查点在预训练和使用减小批量大小进行训练时的遗忘动态。这些结果对使用更大批量大小预训练 LLMs 的优势有几个启示。使用较小批量大小训练的 LLMs 显示出更高的 effectivity,然而衰减常数往往更高。并且使用较小批量大小训练的模型具有较短的可学习性阈值(即 LLM 无法学习间隔超过该阈值所呈现的知识的点),我们将在接下来的 §4.4 中详细讨论。换句话说,当 LLM 使用较小批量大小进行训练时,事实知识应更频繁地呈现给模型,以免被遗忘,带来可学习知识集合变少。其次,与记忆和语义泛化相比,使用较小批量大小时,加速遗忘对组合泛化的影响更为明显。简而言之,结果表明,使用较小批量大小进行预训练由于加速遗忘而减少了可学习的知识集合,并且会导致学习到的事实知识的组合泛化性能较差。
4.4 Implications for LLM pretraining
图 5 中测算的 x 轴截距表示会导致通过训练获得的事实知识完全丢失所需的额外训练 token 数量。因此,如果预训练数据集中的某个给定事实知识位于长尾部分,并且该知识以超过某个阈值的间隔呈现给模型,无论预训练的持续时间如何,该知识都无法被模型学习到。这意味着存在一个可学习阈值,即模型无法获取其遇到间隔超过该阈值的知识。大多数众所周知的事实很可能以训练步骤较短的间隔呈现给模型,短于这个可学习阈值。在这种情况下,随着预训练的进行,模型在每次遇到该知识时会累积其增加的对数概率,并且在某个时刻,该知识的累积对数概率将足够高,从而使模型在解码输出时生成该知识。
我们假设更大且更多样化的预训练数据有助于模型性能的原因是模型可以获取更广泛的事实知识(更多的知识将以短于可学习阈值的间隔呈现),因为随着数据变得更大和更多样化,事实知识流行度的分布倾斜可能会得到缓解。
为什么去重可以提高模型性能?最近的预训练语料库都进行了彻底的去重处理,因为广泛观察到去重可以提高模型性能。我们的结果表明,在 §4.3 中观察到的改写注入场景中较小的衰减常数可以解释使用去重训练数据训练 LLMs 的优势,因为去重倾向于减缓泛化已获取事实知识的遗忘。这在图 2 也可以观察到,注入知识后的对数概率增加的差距在复制和改写注入场景之间很大,但在测量结束时这个差距减小。此外,由于模型倾向于对记忆而不是泛化提供更高的对数概率增加(图 2 和 3),将重复的文本以较短的间隔呈现给模型将导致记忆和泛化之间的差距扩大,这将使模型更倾向于生成记忆的上下文而不是泛化的事实知识。