本文是 《Evaluation Metrics for Language Modeling》 的笔记。
通常情况下,语言模型的性能可以通过困惑度(perplexity)、交叉熵(cross entropy)和每字符比特数(bits-per-character,BPC)来衡量。随着语言模型越来越多地被用作其他自然语言处理任务的预训练模型,它们通常也会根据在下游任务上的表现来进行评估。GLUE 基准分数是对语言模型进行更广泛的多任务评估的一个例子。有趣的是,拥有更多的评估指标实际上使得对比不同语言模型更加困难,尤其是因为这些指标作为衡量语言模型在特定下游任务上表现的指示器往往不可靠。
一个令人困惑的问题是,语言模型通常旨在最小化困惑度,但由于我们无法达到困惑度为零,那么困惑度的下限是多少呢?如果我们不知道最优值,我们如何知道我们的语言模型有多好?
此外,与准确率等指标不同,无论这两个模型是如何训练的,在相同的测试集上,90% 的准确率都明显优于 60% 的准确率。然而,如果我们不知道文本是如何预处理、词汇量、上下文长度等信息,仅仅争论一个模型的困惑度是否小于另一个模型的困惑度并没有太大意义。例如,一个基于字符级别的语言模型的困惑度可能远小于一个基于词级别的模型的困惑度,但这并不意味着字符级别的语言模型就比词级别的模型更好。那么,我们如何比较使用不同符号集的不同语言模型的性能呢?或者我们是否应该进行比较?
尽管存在下游评估基准,传统的内在指标在语言模型训练过程中仍然非常有用。在本文中,我们将重点关注这些内在指标。我们将通过解释这些指标的含义,探索它们之间的关系,建立数学和经验上的界限,并提出关于如何报告这些指标的最佳实践。
Understanding perplexity, bits-per-character, and cross entropy
Language model
考虑一个任意的语言,语言模型为任意符号序列分配概率,使得在该语言中存在的序列获得的概率越高。一个符号可以是一个字符、一个单词或一个子词(例如,单词 ‘going’ 可以被分解为两个子词:’go’ 和 ‘ing’)。大多数语言模型通过每个符号基于其前序符号的条件概率的乘积来估算这个概率:
\[\begin{aligned} P_{(w_1, w_2, ..., w_n)} &= p(w_1)p(w_2|w_1)p(w_3|w_1,w_2)...p(w_n|w_1, w_2, ..., w_{n-1}) \\ &=\prod_{i=1}^np(w_i|w_1,...,w_{i-1}) \end{aligned}\]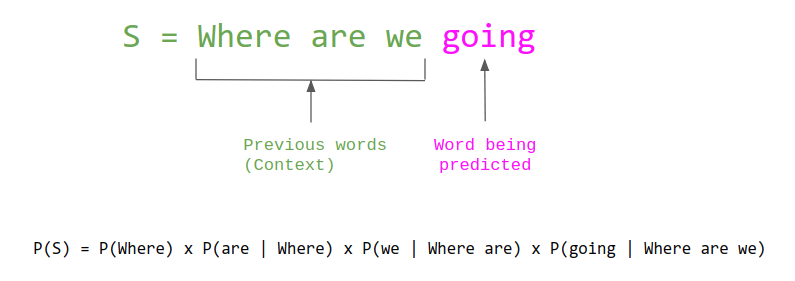
Entropy
任何语言的目标是传达信息。为了衡量在一条信息中传达的平均信息量,我们使用了一种称为“熵”的度量标准,由克劳德·香农(Claude Shannon)提出(《A Mathematical Theory of Communication》)。需要注意的是,语言上下文的熵与热力学上下文的熵相关,但并不完全相同。
对于语言的熵,克劳德·香农在他的重要论文《Prediction and Entropy of Printed English》》中给出了一个直观的解释:
“熵是一种统计参数,以某种意义上衡量了语言中每个字母平均产生多少信息。如果将语言以最高效的方式转换为二进制数字(0 或 1),那么熵就是原始语言中每个字母平均所需的二进制位数。”
我们知道,在 8 位 ASCII 编码中,每个字符由 8 个位组成。然而,这并不是表示英语字母的最高效方式,因为无论字母的常见程度如何,它们都使用相同数量的位来表示(更优化的方案是对常见字母使用较少的位数)。因此,我们应该预期英语语言的字符级熵小于8。
Shannon 通过一个函数 $F_N$ 来近似计算任何语言的熵 $H$,这个函数衡量了跨越 $N$ 个相邻字母的文本的信息量,令 $b_n$ 表示 n 个连续字母 $(w_1, w_2, …, w_n)$ 组成的块:
\[\begin{aligned} F_N &= -\sum_{b_n} p(b_n)\log_2 p(w_n|b_{n-1}) \\ &= -\sum_{b_n} p(b_n)\log_2 \frac{p(b_n)}{p(b_{n-1})} \\ &= -\sum_{b_n}p(b_n)\log_2 p(b_n) + \sum_{b_{n-1}} p(b_{n-1})\log_2 p(b_{n-1}) \end{aligned}\]定义函数 $K_N = -\sum_{b_n}p(b_n)\log_2 p(b_n)$,可得:
\[F_N = K_N - K_{N-1}\]Shannon 定义语言熵 $H$ 为:
\[H = \lim_{N\rightarrow\infty} F_N\]需要注意的是,按照这个定义,熵的计算需要用到无限数量的符号。在实践中,我们只能从有限的文本样本中近似计算经验熵。
Cross entropy
由于语言中缺乏无限量的文本,语言的真实分布是未知的。语言模型的目标是从样本文本中学习一个分布 $Q$,使其接近语言经验分布 $P$。为了度量两个分布之间的”接近程度”,通常使用交叉熵。从数学角度来说,$Q$ 相对于 $P$ 的交叉熵定义如下:
\[H(P, Q) = E_P[-\log Q]\]当 $P$ 和 $Q$ 是离散分布时,这变成:
\[\begin{aligned} H(P, Q) &= -\sum_x P(x)\log Q(x) \\ &= -\sum_x P(x)[\log P(x) + \log Q(x) - \log P(x)] \\ &= -\sum_x P(x)[\log P(x) + \log\frac{Q(x)}{P(x)}] \\ &= -\sum_x P(x)\log P(x) - \sum_x P(x) \log \frac{Q(x)}{P(x)} \\ &= H(P) + D_{KL}(P||Q) \end{aligned}\]其中 $D_{KL}(P||Q)$ 是 $Q$ 相对于 $P$ 的 Kullback-Leibler(KL)散度。这一项也被称为 $P$ 关于 $Q$ 的相对熵。因此,$Q$ 相对于 $P$ 的交叉熵是以下两个值的和:
- 使用针对 $P$ 优化的编码方案[即 $H(P)$,$P$ 的熵]来编码 $P$ 的任何可能结果所需的平均比特数。
- 使用针对 $Q$ 优化的编码方案来编码 $P$ 的任何可能结果所需的额外比特数。
需要注意的是,由于 $H(P)$ 是不可优化的,当我们通过最小化交叉熵损失来训练语言模型时,真正的目标是最小化 KL 散度。
Perplexity
维基百科将困惑度定义为:
“衡量概率分布或概率模型预测样本的效果指标(a measurement of how well a probability distribution or probability model predicts a sample)。”
从直观上理解,困惑度可以被视为不确定性的度量。语言模型的困惑度可以被看作是在预测下一个符号时的不确定程度。考虑一个熵为 3 bits 的语言模型,其中每个比特编码两个等概率的可能结果。这意味着在预测下一个符号时,该语言模型必须在 $2^3=8$ 个可能的选项中进行选择。因此,我们可以说这个语言模型的困惑度为 8。
从数学角度来说,语言模型的困惑度定义为:
\[\text{PPL}(P, Q) = 2^{H(P, Q)}\]Bits-per-character and bits-per-word
每字符比特数(Bits-per-character, BPC)是最近语言模型中经常报告的另一个指标。它测量的正是其名称所指:编码一个字符所需的平均比特数。这引出了对香农关于语言熵的解释的重新审视:
“如果语言以最有效的方式转换为二进制数字(0 或 1),那么熵就是原始语言中每个字母所需的平均二进制位数。”
根据这个定义,熵就是平均的 BPC。
虽然熵和交叉熵是使用以 2 为底的对数(单位为“bit”)定义的,但流行的机器学习框架,包括 TensorFlow 和 PyTorch,使用自然对数(单位为“nat”)来实现交叉熵损失。这是因为计算自然对数比计算以 2 为底的对数更快。从理论上讲,对数的底数并不重要,因为差异是一个固定的比例:
\[\frac{\log_e n}{\log_2 n} = \frac{\log_e 2}{\log_e e} = \ln 2\]请记住,BPC 是特定于字符级语言模型的。当我们有词级语言模型时,这个量被称为 BPW(每词比特数)——编码一个词所需的平均比特数。
Reasoning about entropy as a metric
由于我们可以在困惑度和交叉熵之间进行转换,从本节开始,我们将只研究交叉熵。
对于许多用于机器学习模型的指标,我们通常知道它们的界限。例如,准确率的最佳可能值是 100%,而单词错误率和均方误差的最佳值是 0。如果我们的模型达到 99.9999% 的准确率,我们可以相当确定地知道我们的模型已经非常接近其可能达到的最佳表现。
然而,当有人声称一个语言模型的交叉熵损失为 7 时,如果我们不知道最佳可能结果应该是什么,我们就不知道它离最佳结果有多远。不知道我们要达到的目标可能会使我们在决定投入多少资源以期改进模型时面临挑战。
Mathematical bounds
首先,我们知道任何分布的可能的最小熵是零。然而,只有当一种语言只有一个符号时,该语言的熵才可能为零。
\[\min H(P) = -1 * \log(1) = 0\]如果一种语言有两个字符且它们出现的概率相等,那么它的熵将是
\[H(P) = -0.5 * \log(0.5) - 0.5 * \log(0.5) = 1\]其次,我们知道,当概率分布是均匀时,其熵达到最大。这暗示了对于所有共享相同符号集(词汇)的语言来说,熵最大的语言是所有符号出现概率相等的语言。设 $|V|$ 为具有分布 $P$ 的任意语言的词汇量:
\[H(P) \leq -|V| * \frac{1}{|V|} * \log(\frac{1}{|V|}) = -\log \frac{1}{|V|} = \log (|V|)\]如果我们将英语视为一种包含 27 个符号的语言(即英文字母加上空格),那么其字符级熵最多为:
\[\log(27) = 4.7549\]一个 20 岁左右的美国人平均知道 42,000 个单词,因此他们的词汇级熵最多为:
\[\log(42000) = 15.3581\]我们知道语言模型的交叉熵损失至少等于该语言模型所训练文本的经验熵。如果底层语言的经验熵为 7,那么交叉熵损失至少为 7。
证明:设 $P$ 为底层语言的分布,$Q$ 为语言模型学习到的分布。根据定义:
\[H(P, Q) = H(P) + D_{KL}(P||Q)\]因为 $D_{KL}(P||Q) \geq 0$,可得 $H(P, Q) \geq H(P)$。
最后,请记住,根据香农的定义,熵是当 $N$ 趋于无穷大时的 $F_N$ 值。我们将展示随着 $N$ 的增加,$F_N$ 的值会减少。直观上,这很有道理,因为前面的序列越长,模型在预测下一个符号时就越不容易困惑。
以下证明对于所有 $N \geq 1$ ,都有 $F_{N+1} \leq F_N$。假设每个字符 $w_i$ 来自一个包含 $m$ 个字母 $x_1, x_2, …x_m$ 的词汇表。请记住,$F_N$ 衡量的是统计覆盖文本中相邻的 N 个字母而产生的信息量或熵。
\[\begin{aligned} F_N - F_{N+1} &= -\sum_{b_n} p(b_n)\log p(w_n|b_{n-1}) + \sum_{b_{n+1}} p(b_{n+1}) \log p(w_{n+1}|b_n) \\ &= \sum_{b_{n-1}}[\sum_{w_n, w_{n+1}}p(b_{n+1})\log p(w_{n+1}|b_n) - \sum_{w_n} p(b_n)\log p(w_n|b_{n-1})] \\ &\geq \sum_{b_{n-1}}[\sum_{w_n, w_{n+1}}p(b_{n+1})\log p(w_{n+1}|b_{n-1}) - \sum_{w_n} p(b_n)\log p(w_n|b_{n-1})] \\ &= \sum_{b_{n-1}}[\sum_{w_n, w_{n+1}}p(b_{n-1}, w_n, w_{n+1})\log p(w_{n+1}|b_{n-1}) - \sum_{w_n} p(b_{n-1}, w_n)\log p(w_n|b_{n-1})] \\ &= \sum_{b_{n-1}}[\sum_{w_{n+1}}\log p(w_{n+1}|b_{n-1})\sum_{w_n}p(b_{n-1}, w_n, w_{n+1})- \sum_{w_n} p(b_{n-1}, w_n)\log p(w_n|b_{n-1})] \\ &= \sum_{b_{n-1}}[\sum_{w_{n+1}}\log p(w_{n+1}|b_{n-1})p(b_{n-1}, w_{n+1})- \sum_{w_n} p(b_{n-1}, w_n)\log p(w_n|b_{n-1})] \\ &= 0 \end{aligned}\]第三行的等式是因为 $\log p(w_{n+1}|b_n) \geq \log p(w_{n+1}|b_{n-1})$。最后一个等式是因为 $w_n$ 和 $w_{n+1}$ 来自相同的域。 因此:
\[F_1 \geq F_2 \geq ... \geq \lim_{N \rightarrow \infty} F_N = H(P)\]这意味着,对于无限量的文本,使用较长上下文长度的语言模型通常应该比使用较短上下文长度的模型具有更低的交叉熵值。对于有限量的文本,这可能会变得复杂,因为语言模型可能没有看到足够长的序列来做出有意义的预测。
建议:在报告语言模型的困惑度或熵时,我们应该指定上下文长度。
Estimated bounds
测算书面英文熵的主要方法有两种:人类预测和压缩。
Human predictions
这种方法假设任何语言的使用者都拥有该语言的大量统计知识,使他们能够根据前面的文本猜测下一个符号。根据猜测正确结果所需的次数,香农推导出了熵的上下界估计。他从普利策奖获奖的六卷本系列《杰斐逊与他的时代》的第一卷《弗吉尼亚人杰斐逊》中随机选择了 100 个样本,每个样本包含 100 个字符。他使用了 26 个符号的字母表(英文字母)和 27 个符号的字母表(英文字母加空格):

Compression
在语言建模的背景之外,BPC 建立了压缩的下限。如果一段文本的 BPC 为 1.2,则无法压缩到每字符少于 1.2 bits。例如,如果文本有 1000 个字符(如果每个字符用 1 字节表示,大约为 1000 字节),其压缩版本至少需要 1200 bits 或 150 字节。
反过来,如果我们有一个最优的压缩算法,我们可以通过压缩所有可用的英语文本并测量压缩数据的位数来计算书文英语的熵。
1996 年,Teahan 和 Cleary 使用部分匹配预测(prediction by partial matching,PPM),这是一种自适应统计数据压缩技术,利用未压缩流中不同长度的前一个符号来预测下一个符号。Teahan 和 Cleary 使用固定的五阶模型(使用最多五个前一个符号进行预测)和 27 符号的字母表,在 Dumas Malone 的《弗吉尼亚人杰斐逊》的最后一章中实现了 1.461 的 BPC。
2006年,Hutter 奖启动,目标是压缩 enwik8。截至 2019 年 4 月,获胜者仍然是 Alexander Rhatushnyak,他实现了 6.54 的压缩比,相当于约 1.223 BPC。2019 年 1 月,Dai 等人使用一种称为 Transformer-XL 的神经网络架构训练了一个语言模型,在 enwik8 上实现了 0.99 的 BPC。
Comparing perplexities across language models
到目前为止,我们只探讨了字符级别的熵。然而,也存在词级和子词级的语言模型,这引发了我们对相关问题的思考。是否可以比较具有不同符号类型的语言模型的熵?换句话说,我们能否在字符级熵和词级熵之间进行转换?
Graves 使用了这个简单的公式:如果平均而言,一个单词需要 $m$ 位来编码,并且一个单词包含 $l$ 个字符,那么平均而言,编码一个字符应需要 $\frac{m}{l}$ 位。在其论文《Generating Sequences with Recurrent Neural Networks》中,由于数据集中一个单词平均有 5.6 个字符,词级困惑度的计算公式为:$2^{5.6*BPC}$。
香农使用了类似的推理。通过 Zipf’s law,该定律指出“任何单词的频率与其在频率表中的排名成反比”,香农近似估计了英语单词的频率,并估测词级 $F_1$ 为 11.82。假设平均英语单词长度为 4.5,人们可能会倾向于将值 $\frac{11.82}{4.5} = 2.62$ 应用于字符级 $F_4$ 和 $F_5$ 之间。
然而,2.62 实际上位于字符级 $F_5$ 和 $F_6$ 之间。香农认为,原因在于“一个单词是一个具有强内部统计影响的字母群,因此单词内部的 N-gram 比跨单词的 N-gram 更受限制。
对于词级 $F_N$,当 $N \geq 2$ 时,单词边界问题不再存在,因为空格现在是多词短语的一部分。因此,如果我们的词级语言模型处理长度 $N \geq 2$ 的序列,我们应该可以通过将该值除以平均单词长度,将词级熵转换为字符级熵。
建议:在报告语言模型的困惑度或熵时,我们应该明确说明是词级、字符级还是子词级。
Empirical entropy
在本节中,我们将计算数据集 SimpleBooks、WikiText 和 Google Books 的经验字符级熵和词级熵。
WikiText 是从维基百科上知识丰富和特色的文章列表中提取的。它包含 1.03 亿个词级 token,词汇量为 22.9 万个 token。词汇表中仅包含至少出现 3 次的 token——罕见的 token 被替换为 <unk> token。
SimpleBooks 是从 1,573 本 Gutenberg 图书中创建的,这些图书具有较高的长度与词汇比。它有 9,200 万个词级 token,但词汇量仅为 9.8 万,unk token 仅占 0.1%。
Google Books 数据集来自谷歌,截至 2008 年出版的 500 多万本书。它以词级 N-gram 的形式提供,其中 $1 \leq N \leq 5$。我们检查了所有的词级 5-gram,以获得字符级 N-gram,其中 $1 \leq N \leq 9$。
我们从这些数据集中移除了所有包含了标准 27 字母表之外字符的 N-gram。对于 Google Books 数据集,我们分析了词级 5-gram 以获得字符 N-gram,其中 $1 \leq N \leq 9$。有关这些数据集的经验熵,请参见表 4、表 5 和图 3。
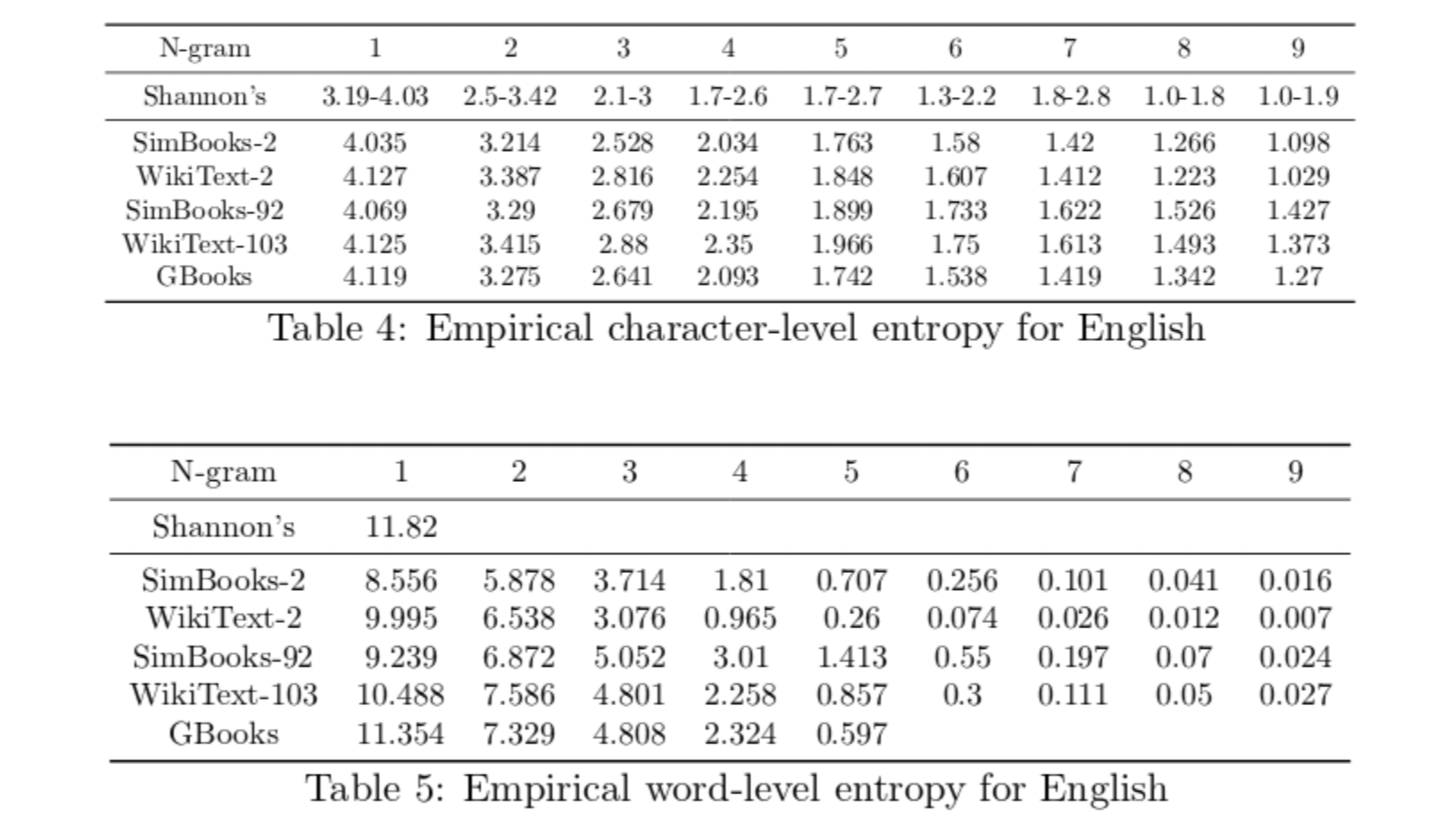
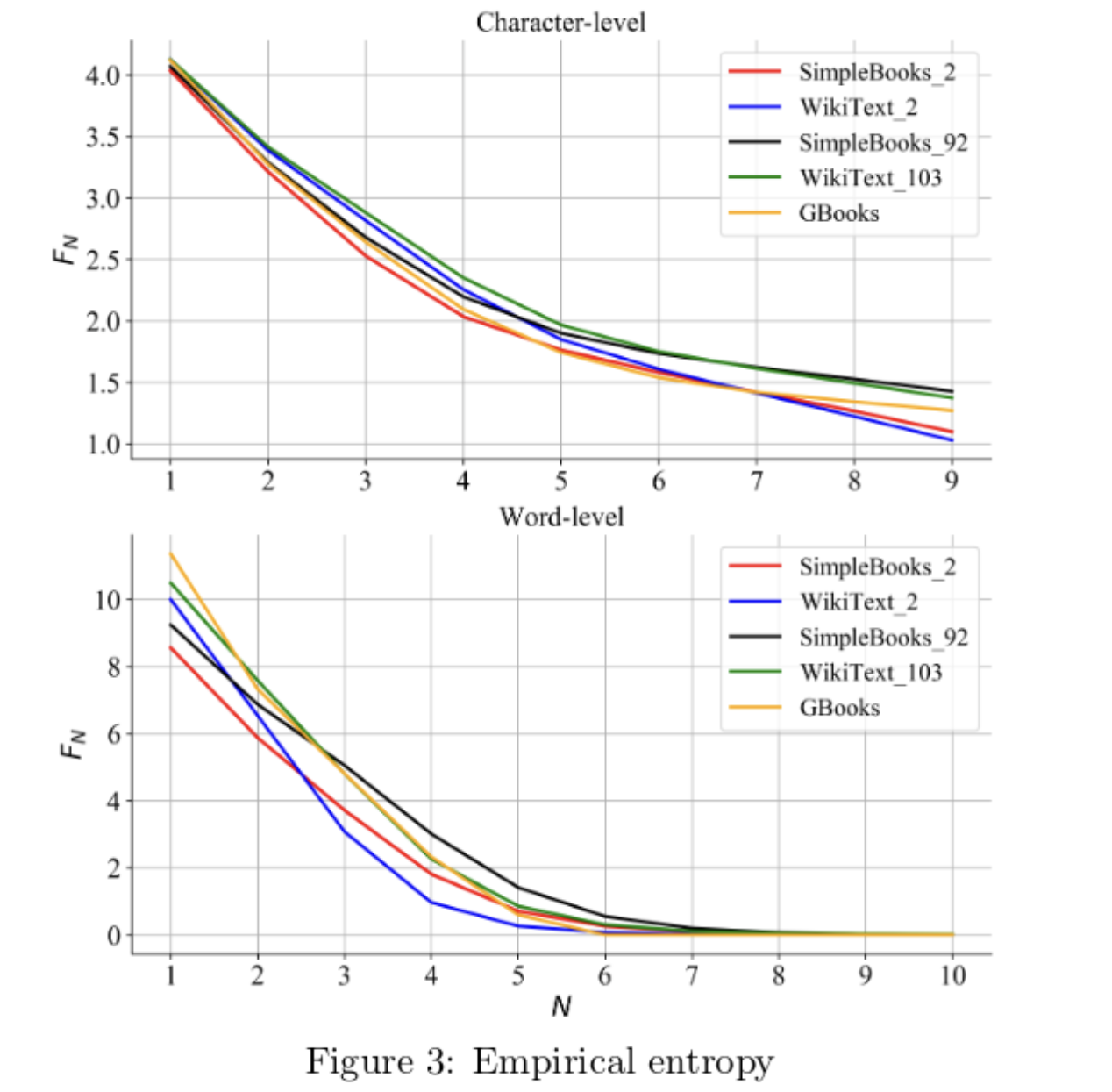
首先需要注意的是,考虑到香农在 1950 年所拥有的有限资源,他对熵的估计是多么的出色。大多数经验 F 值正好落在香农预测的范围内,除了 1-gram 和7-gram 字符熵。香农对 7-gram 字符熵的估计很独特,因为它高于他对 6-gram 字符的估计,这与之前证明的恒等式相矛盾。
这些数据集的经验 F 值有助于解释为什么容易对某些数据集过拟合。例如,WikiText-2 的字符级和词级 F 值随着 N 的增加迅速下降,这解释了为什么容易对该数据集过拟合。SimpleBooks-92 的 F 值下降得最慢,这解释了为什么更难对该数据集过拟合,因此该数据集上的 SOTA 困惑度是最低的(见表5)。
Neural networks versus N-grams language models
上一节中的值是使用香农提出的公式计算的内在 F 值。在本节中,我们将旨在比较词级 n-gram 语言模型和神经语言模型在 WikiText 和 SimpleBooks 数据集上的表现。请参见表 6:
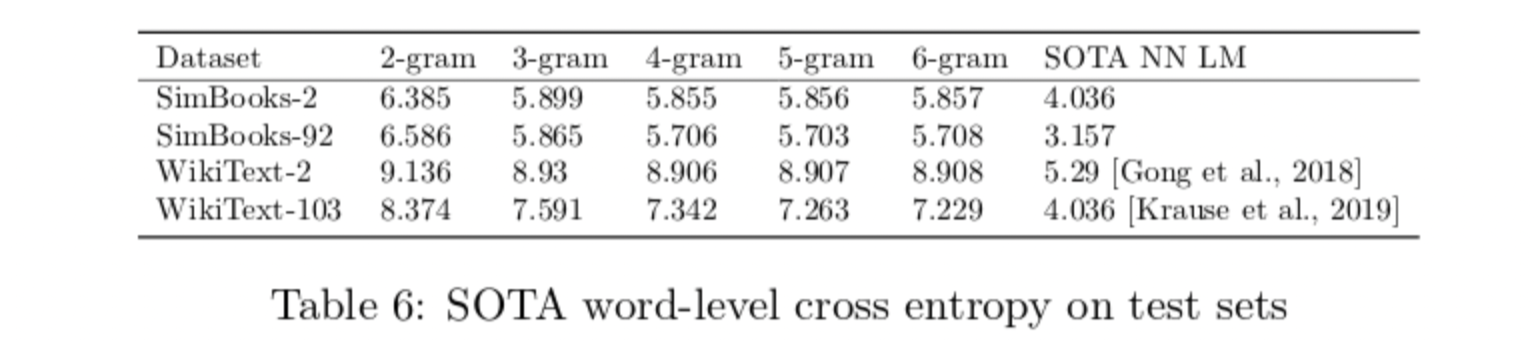
对于 N-gram 语言模型我们使用 KenLM,对于神经语言模型,我们使用已发布的 WikiText 的 SOTA 和 Transformer-XL 来处理 SimpleBooks-2 和 SimpleBooks-92。这将通过在两个数据集的测试集上计算交叉熵来完成。请注意,虽然神经语言模型的 SOTA 熵与英语文本的经验熵依然相差甚远,但它们的表现远优于 N-gram 语言模型。当 N 超过 4 时,N-gram 语言模型的性能没有太大改善,而神经语言模型的性能随着时间的推移不断提高。在不到两年的时间里,WikiText-103 上神经语言模型的 SOTA 困惑度从 40.8 降至 16.4:
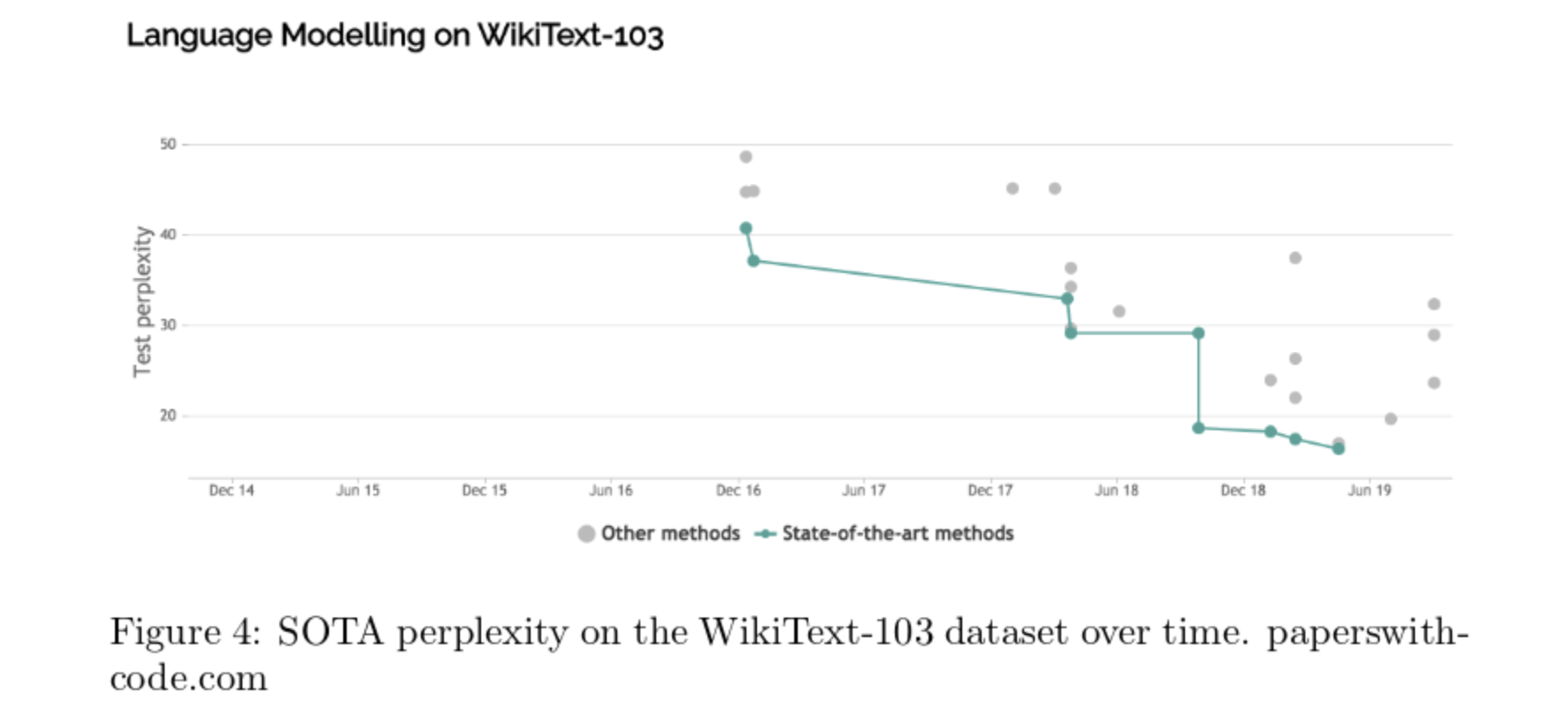
The future of language modeling and language modeling evaluations
随着语言模型越来越多地用于迁移学习到其他自然语言处理任务,语言模型的内在评估不如其在下游任务上的表现重要。一些下游任务已被证明能显著受益于预训练语言模型,包括情感分析、文本蕴涵识别和释义检测。目前已经有多个 benchmark 用以评估模型在一组下游任务上的表现,包括 GLUE、SuperGLUE 和 decaNLP。论文很少发布其语言模型的交叉熵损失与其在下游任务上表现之间的关系,也没有研究它们的相关性。在论文《XLNet: Generalized Autoregressive Pretraining for Language Understanding》中,作者声称语言模型性能的提升并不总是会带来下游任务的改进:
“可以观察到模型在训练结束时仍然对数据欠拟合,但继续训练并没有帮助下游任务,这表明在给定的优化算法下,模型没有足够的能力充分利用数据规模。”
然而,困惑度仍然是一个有用的指标。论文《RoBERTa: A Robustly Optimized BERT Pretraining Approach》表明,对于掩码语言建模目标,较好的“困惑度”会带来情感分析和多类型自然语言推理任务的“最终任务准确性”更高。不过,RoBERTa 与目前在最受欢迎的基准 GLUE 排行榜上排名前五的其他模型类似,并不是在传统的语言建模任务上进行预训练的,而是在完形填空任务上。对于这个任务,困惑度从未被定义,但可以假设有左右上下文应该使预测更容易。
尽管有其他方法可以评估语言模型的性能,但困惑度依然是一个简单、多功能且强大的指标,不仅可以用于评估语言建模,还可以用于任何使用交叉熵损失的生成任务,如机器翻译、语音识别、开放域对话。