本文是 《Prediction and Entropy of Printed English》 的部分笔记。
Introduction
熵是一种统计参数,从某种意义上衡量了在该语言的文本中,每个字母平均产生多少信息。如果将语言以最有效的方式转换为二进制数字(0 或 1),那么熵就是原始语言中每个字母平均所需的二进制位数。另一方面,冗余度衡量的是由于语言的统计结构对文本施加的约束量,例如,在英语中,字母 E 的高频率,H 紧随 T 之后或 V 紧随 Q 之后的强烈倾向。据估计,当考虑不超过八个字母的统计效应时,熵大约是每个字母 2.3 bits,冗余度约为 50%。
自那时以来,已经找到了一种新的方法来估计这些量,这种方法更为灵敏,并考虑了长程(long range)的统计,即延伸到短语、句子等的统计。这种方法基于对英语可预测性的研究:当已知前面的 N 个字母时,文本的下一个字母能被多准确地预测。论文将给出一些预测实验的结果,并对理想预测的一些性质进行理论分析。通过结合实验和理论结果,可以估计熵和冗余度的上下界。从这一分析来看,在普通文学英语中,长程统计效应(长达 100 个字母)将熵降低到每个字母大约 1 bit,相应的冗余度大约为 75 %。当延伸到段落、章节等的结构时,冗余度可能更高。然而,随着涉及的长度增加,相关参数变得更加不稳定和不确定,并且它们更依赖于所涉及文本的类型。
ENTROPY CALCULATION FROM TIIK STATISTICS OF ENGLISH
计算熵 $H$ 的一种方法是通过一系列近似值 $F_0, F_1, F_2, …$,这些近似值逐步考虑了越来越多的语言统计,逐渐逼近 $H$。$F_N$ 可以称为 N-gram 熵;它衡量的是文本中 $N$ 个相邻字符产生的信息量或熵。
\[\begin{aligned} F_N &= - \sum_{i,j}p(b_i, j)\log_2 p_{b_i}(j) \\ &= - \sum_{i,j}p(b_i, j)\log_2 p(b_i, j) + \sum_i p(b_i)\log p(b_i) \end{aligned} \tag{1}\]其中 $b_i$ 是由 N - 1 个字母(N-1 gram)组成的,$j$ 是 $b_i$ 后的任意字母,$p(b_i , j)$ 是 N-gram $b_i$, $j$ 的概率。$p_{b_i}(j)$ 是字母 $j$ 在块 $b_i$ 之后的条件概率,为 $p(b_i, j)/p(b_i)$。
方程(1)可以解释为在已知前 N − 1 个字母的情况下,测量下一个字母 $j$ 的平均不确定性(条件熵)。随着 N 的增加,$F_N$ 包含越来越长程的统计,熵 $H$ 由 $F_N$ 在 $N\rightarrow \infty$ 时的极限值给出:
\[H = \lim_{N\rightarrow \infty}F_N \tag{2}\]对于较小的 N 值,N-gram 熵 $F_N$ 可以从字母、二元组和三元组的频率数据表(《Secret and Urgent》)计算得出。如果忽略空格和标点符号,我们有一个由 26 个字母组成的字母表,并且 $F_0$ 可以(根据定义)取为 $\log_2 26$,即每个字母 4.7 比特。$F_1$ 涉及字母频率,其值为:
\[F_1 = - \sum_{i=1}^{26} p(i)\log_2 p(i) = 4.14~\text{bits per letter} \tag{3}\]二元组近似 $F_2$ 结果如下:
\[\begin{aligned} F_2 &= -\sum_{i,j}p(i, j)\log_2p_i(j) \\ &= -\sum_{i, j}p(i, j)\log_2p(i, j) + \sum_ip(i)\log_2p(i) \\ &= 7.7 - 4.14 = 3.56 ~\text{bits per letter} \end{aligned} \tag{4}\]三元组熵由以下公式给出:
\[\begin{aligned} F_3 &= - \sum_{i,j,k}p(i, j, k)\log_2p_{ij}(k) \\ &= -\sum_{i,j,k}p(i, j, k)\log_2p(i, j, k) + \sum_{i, j}p(i, j)\log_2 p(i, j) \\ &= 11.0 - 7.7 = 3.3 \end{aligned} \tag{5}\]在此计算中,所使用的三元组表没有考虑跨越两个单词的三元组,例如在 ‘TWO WORDS’ 中的 ‘WOW’ 和 ‘OWO’。为了部分弥补这一遗漏,通过以下公式从表中的概率 $p’(i,j,k)$ 获得粗略修正后的三元组概率 $p(i,j,k)$:
\[p(i, j, k) = \frac{2.5}{4.5}p'(i, j, k) + \frac{1}{4.5}r(i)p(j, k) + \frac{1}{4.5}p(i, j)s(k)\]其中 $r(i)$ 是字母 $i$ 作为单词结尾字母的概率,$s(k)$ 是字母 $k$ 作为首字母的概率。因此,单词内的三元组(平均每个单词 2.5 个)根据表格进行计数;跨越单词的三元组(每个单词每种类型一个)通过假设一个单词的结尾字母与下一个单词的首二元组相互独立(反之亦然)来进行近似计数。由于这里涉及近似以及抽样误差,$F_3$ 的值更不可靠。
由于 N-gram 频率表在 $N > 3$ 时不可用,因此无法以相同方式计算 $F_4, F_5$ 等。然而,单词频率已经被整理成表格,可以用于进一步的近似。图 1 是在 log-log 纸上绘制的单词概率与频率排名的关系图。最常见的英语单词 “the” 的概率为 0.071,并绘制在 1 的位置。下一个最常见的单词 “of” 的概率为 0.034,并绘制在 2 的位置,等等。概率和排名都使用对数刻度,曲线大约是一条斜率为 -1 的直线;因此,如果 $p_n$ 是第 $n$ 个最常见单词的概率,我们大致有
\[p_n = \frac{0.1}{n} \tag{6}\]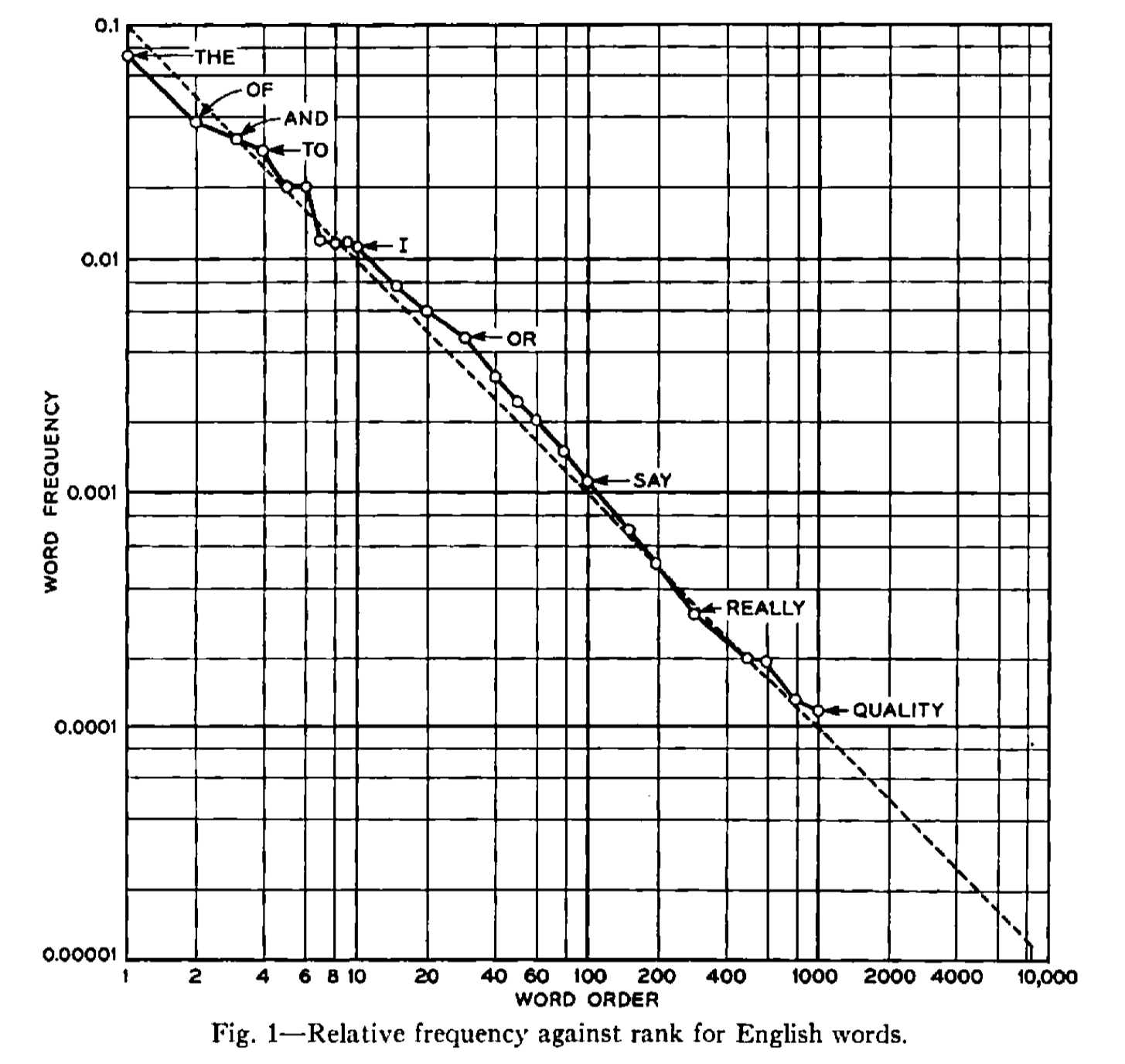
《Human behavior and the principle of least effort》) 指出,这种形式的公式,$p_n= k/n$ 在许多不同语言中对单词概率提供了相当好的近似。公式 (6) 显然不能无限制地成立,因为总概率 $\sum p_n$ 必须为 1,而 $\sum_1^{\infty} .1/n$ 是无穷大的。如果我们假设(在没有更好估计的情况下)公式 $p_n= .1/n$ 成立直到总概率为 1 的 $n$,并且对于更大的 $n$,$p_n= 0$,我们发现临界 $n$ 是排名为 8,727 的单词。那么熵就是:
\[-\sum_1^{8727}p_n \log_2 p_n = 11.82~\text{bits per word}\]或者 11.82/4.5 = 2.62 比特每个字母(英语中平均单词长度是 4.5 个字母)。人们可能会倾向于将这个值等同于 $F_{4.5}$,但实际上在 $N= 4.5$ 时,$F_N$ 曲线的纵坐标会高于这个值。原因是 $F_4$ 或 $F_6$ 涉及四个或五个字母的组合,而不考虑单词划分。一个单词是一个具有强烈内部统计影响的字母的凝聚群体,因此单词内的 N-gram 比跨越单词的 N-gram 更受限制。其结果是,我们在每个字母 2.62 比特中获得的估计更接近于 $F_5$ 或 $F_6$。
将空格作为一个额外的字母,形成一个由 27 个字母组成的字母表,并进行了类似的一组计算。以下是 26 个字母和 27 个字母计算的结果总结:
| $F_0$ | $F_1$ | $F_2$ | $F_3$ | $F_{word}$ | |
| 26 letter | 4.70 | 4.14 | 3.56 | 3.3 | 2.62 |
| 27 letter | 4.76 | 4.03 | 3.32 | 3.1 | 2.14 |
由于当涉及一个或多个单词的序列时,空格符号几乎是完全冗余的,因此当 $N$ 足够大时,27 个字母情况下的 $F_N$ 值将是 26 个字母的 $F_N$ 的 0.818。
PREDICTION OF ENGLISH
这种估算熵的新方法利用了这样一个事实:任何使用某种语言的人都隐含地掌握着该语言的大量统计特性。对单词、习语、陈词滥调和语法的熟悉使人能够在校对时填补缺失或错误的字母,或在对话中完成未完成的短语。可以通过以下实验来展示英语的可预测程度:
选择一段预测者不熟悉的短文。然后要求他猜测文章的第一个字母。如果猜对了,就告诉他正确,然后继续猜测第二个字母。如果猜错了,就告诉他正确的第一个字母,然后进行下一个猜测。随着实验的进行,受试者会写下当前位置之前的正确文本,用于预测后续的字母。
1
2
3
4
5
6
(1) THE ROOM WAS NOT VERY LIGHT ASMALL OBLONG
(2) ----ROO------NOT-V-----I-----SM----OBL----
(1) READING LAMP ON THE DESK SHED GLOW ON
(2) REA----------O------D----SHED-GLO--O--
(1) POLISHED WOOD BUT LESS ON THE SHABBY RED CARPET
(2) P-L-S-----O---BU--L-S--O------SH--··-RE--C------
在总共 129 个字母中,89 个(或 69%)被正确猜测。正如预期的那样,错误最常出现在单词和音节的开头,因为在这些位置思维路径有更多分支的可能性。人们可能会认为第二行(我们称之为简化文本)比第一行包含的信息要少得多。实际上,两行都包含相同的信息,因为至少在理论上可以从第二行恢复出第一行。
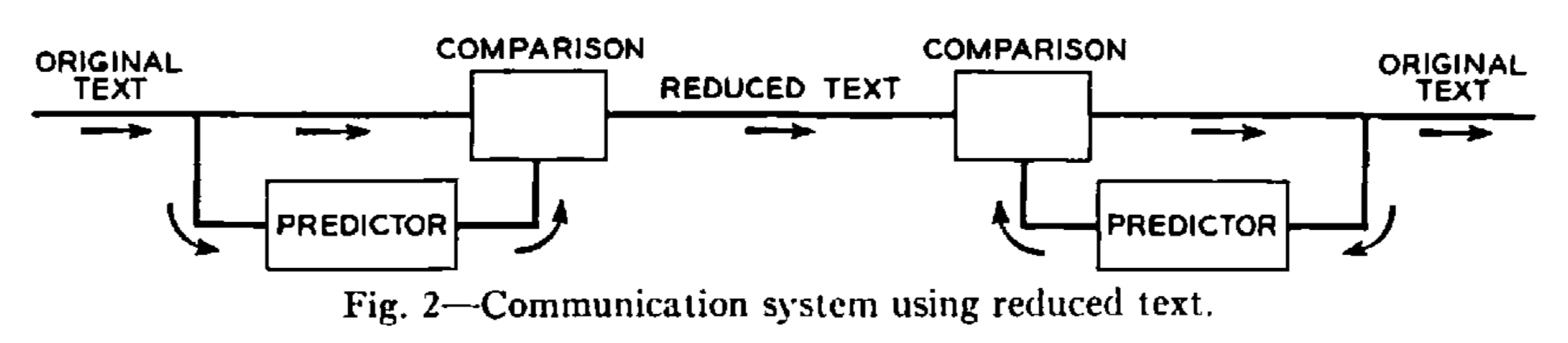
简化文本可以被视为原始文本的一种编码形式,是原始文本通过可逆转换器处理的结果。实际上,可以构建一个通信系统,其中两点之间只传输简化文本。这可以如图 2 所示进行设置,使用两个相同的预测设备。
对上述实验的扩展可以获得关于英语可预测性的更多信息。和之前一样,受试者知道当前位置之前的文本,并被要求猜测下一个字母。如果猜错了,就告诉他错了,让他重新猜测。这个过程持续到他找到正确的字母为止。实验结果如下所示。第一行是原始文本,第二行的数字表示在第几次猜测时得到正确的字母。

在 102 个符号中,受试者 79 次在第一次就猜对,8 次在第二次猜对,3 次在第三次猜对,第四次和第五次各猜对 2 次,只有 8 次需要超过五次猜测。这样的结果是一个具备良好预测能力的受试者在普通文学英语上的典型表现。报纸写作、科学工作和诗歌通常会导致稍微较差的预测结果。
在这种情况下,简化文本同样包含与原始文本相同的信息。简化文本可以被视为原始文本的编码版本。原始语言使用 27 个符号的字母表(A、B、…、Z 和空格),已被转换成使用数字 1、2、…、27 作为字母表的新语言。这种转换使得符号 1 现在具有极高的出现频率。符号 2、3、4 的出现频率逐渐降低,而最后的符号 20、21、…、27 出现得非常罕见。因此,这种转换在很大程度上简化了所涉及的统计结构的性质。原本出现在字母组之间复杂约束中的冗余,通过转换过程,在很大程度上通过新符号的极不均等的概率得到了明确体现。正如后面将会看到的,这使得我们能够从这些实验中估算熵。
为了确定可预测性如何依赖于受试者已知的前 N 个字母数量,进行了一个更复杂的实验。从一本书中随机选取了一百个英文文本样本,每个样本长度为十五个字母。要求受试者像前面的实验一样,对每个样本逐字母进行猜测。这样就获得了一百个样本,其中受试者可以使用 0、1、2、3、…、14 个前序字母。
这些结果,连同另一个已知 100 个字母的类似测试,在表 1 中进行了总结。
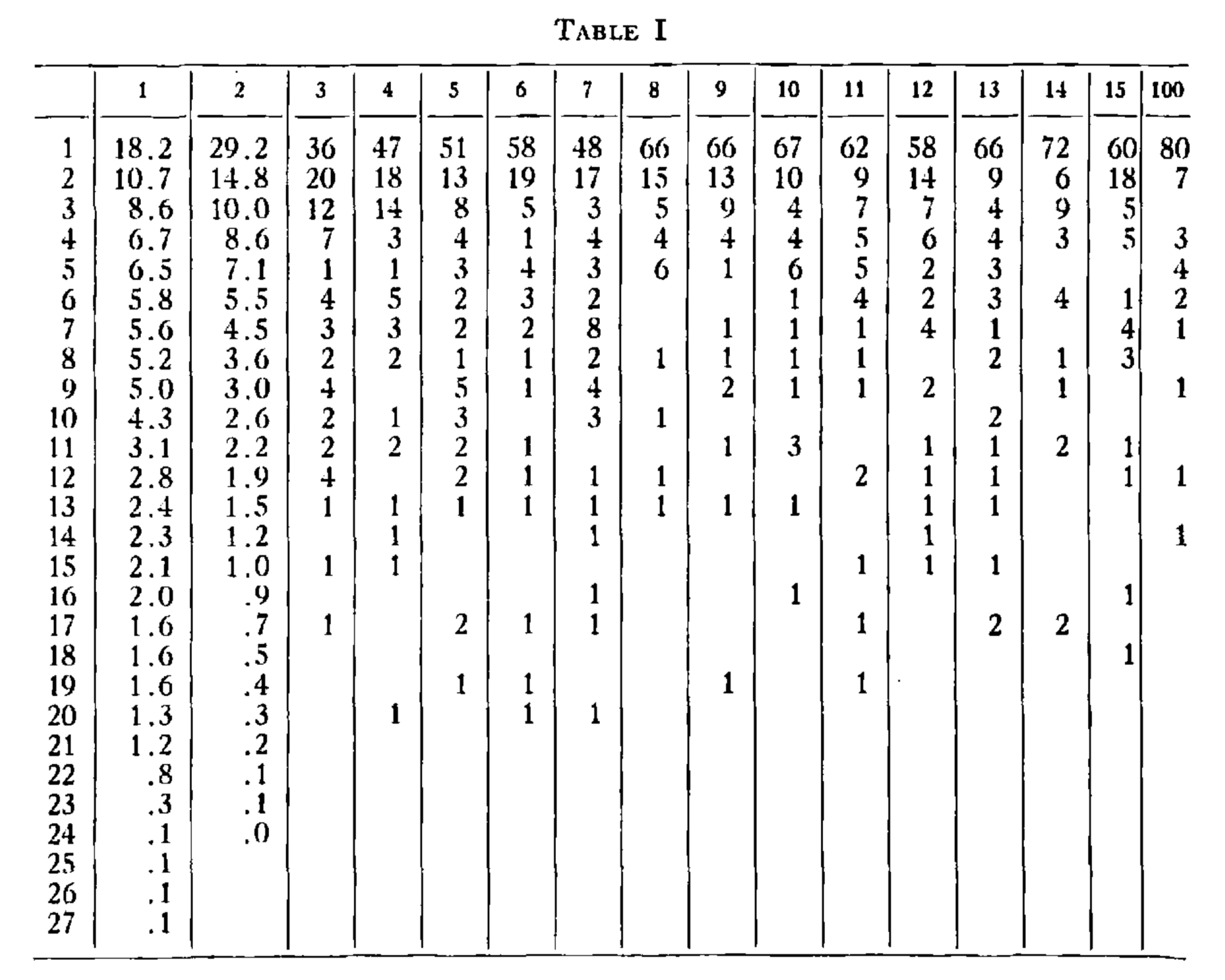
列数对应受试者已知的前序字母数加一;行数是猜测次数。在第 N 列第 S 行的条目表示当已知 (N-1) 个字母时,受试者在第 S 次猜测时猜对的次数。例如,第 6 列第 2 行的数字 19 表示,在已知五个字母的情况下,在一百次中有十九次是在第二次猜测时得到正确字母。 该表的前两列并非通过上述实验程序获得,而是直接从已知的字母和二元组频率计算得出。因此,在不知道任何字母的情况下,最可能的符号是空格(概率 0.182);如果这是错的,下一个猜测应该是 E(概率 0.107),依此类推。这些概率是在最佳预测情况下,正确猜测会在第一次、第二次等尝试中出现的频率。由于频率表是从英语的长样本中确定的,这两列比其他列受到的采样误差更小。
从结果表可以看到,除了一些统计波动外,随着对过去的了解增加,预测逐渐改善,这表现在首次正确猜测数量增加和高排名猜测数量减少。 除此之外,还进行了一个“反向”预测的实验,受试者猜测已知字母之前的字母。尽管这个任务在主观上更加困难,但得分只稍微较差。
因此,从同一来源获得两个101个字母的样本,受试者得到了以下结果:
| No. of guess | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | > 8 |
| Forward | 70 | 10 | 7 | 2 | 2 | 3 | 3 | 0 | 4 |
| Reverse | 66 | 7 | 4 | 4 | 6 | 2 | 1 | 2 | 9 |
顺便提一下,反向语言的 N-gram 熵 $F_N$ 等于正向语言的 N-gram 熵,这可以从方程(1)的第二种形式中看出。在正向和反向情况下,这两个项的值是相同的。