本文是 《Transformer Feed-Forward Layers Are Key-Value Memories》 的笔记。
前馈层占据了 Transformer 模型参数的三分之二,然而它们在网络中的作用仍未得到充分探索。我们展示了基于 Transformer 的语言模型中的前馈层作为键-值记忆的功能,其中每个键与训练示例中的文本模式相关联,每个值引导输出词汇的分布。我们的实验证明学习到的模式是可解释的,并且较低层往往捕捉到浅层模式,而较高层学习到更语义化的模式。值通过引导输出分布来补充键的输入模式,使概率集中在可能紧随每个模式之后出现的 token 上,尤其是在较高层。最后,我们证明前馈层的输出是其记忆的组合,通过残差连接在模型的各层中进行进一步的优化,以产生最终的输出分布。
Introduction
我们展示了前馈层模拟神经记忆,其中层中的第一个参数矩阵对应于键,第二个参数矩阵对应于值。图 1 显示了键(第一个参数矩阵)如何与输入进行交互以产生系数,然后使用这些系数计算值(第二个参数矩阵)的加权和作为输出。虽然前馈层和键值记忆之间的理论相似性之前已经由 Sukhbaatar 等人(2019)提出,但我们进一步观察并分析了前馈层存储的“记忆”。
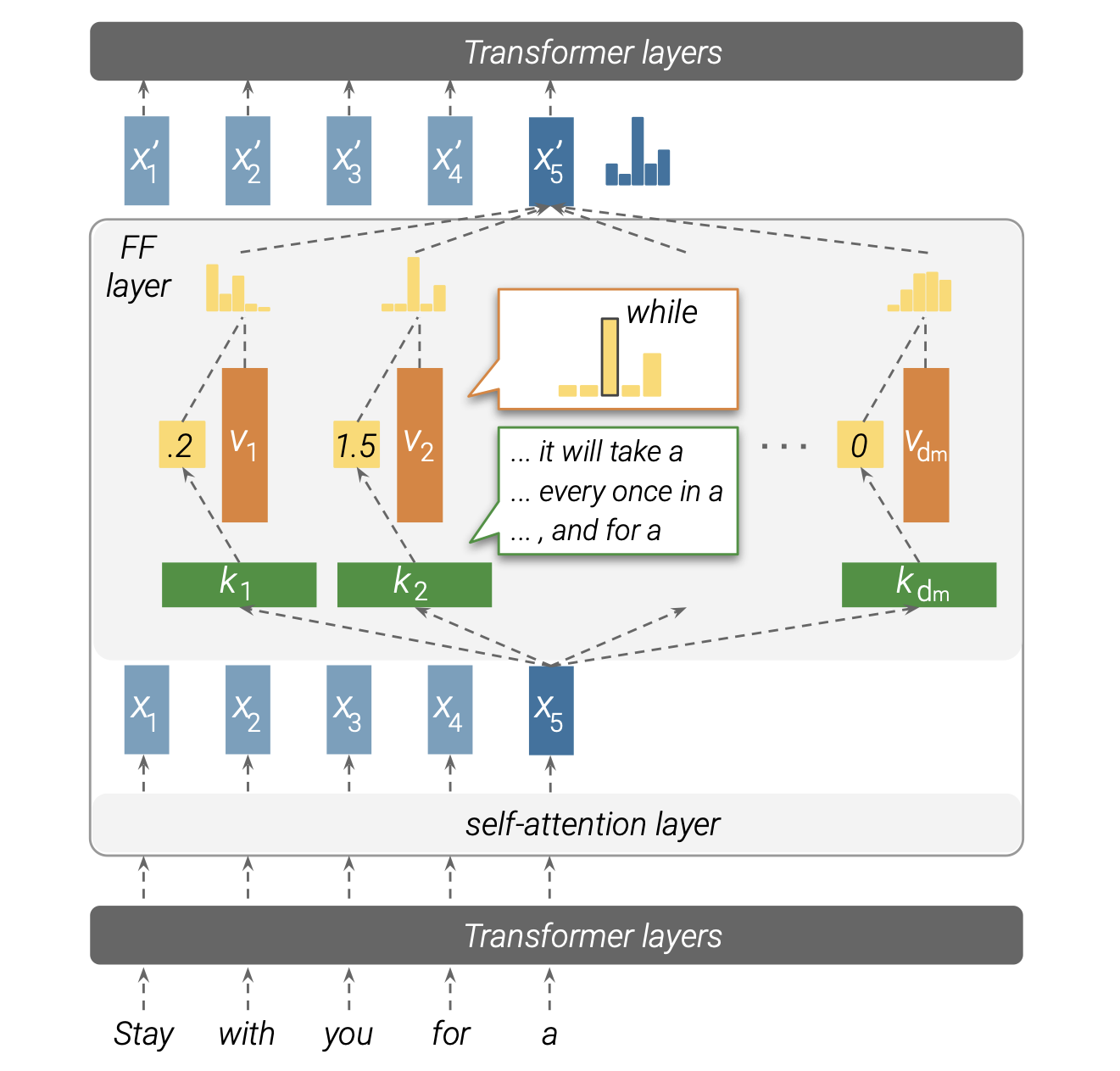
图 1:展示了前馈层如何模拟键值记忆的示意图。输入向量(这里是 $\mathbf{x}_5$)与键相乘,产生记忆系数(例如,$\mathbf{v}_1$ 的记忆系数为 0.2),然后对输出词汇表中存储的值进行加权分布。因此,前馈层的输出是其值的加权和。
我们发现每个键与一组特定的可解释的输入模式相关,例如 n-gram 或语义主题。同时,我们观察到每个值可以引导输出词汇的分布,并且在模型的上层中,这个分布与对应键的下一个 token 分布相关。
最后,我们分析了语言模型如何从各个记忆中构建其最终预测。我们观察到每一层都结合了数百个活跃的记忆,形成的分布与其各个记忆的值有显著不同。同时,层与层之间的残差连接起到了精细调整机制的作用,在保留大部分残差信息的同时,轻微地调整每一层的预测。
总的来说,我们的工作揭示了 Transformer 语言模型中前馈层的功能。我们展示了前馈层在所有层上都充当输入的模式检测器,并且最终的输出分布是以自下而上的方式逐渐构建的。
Feed-Forward Layers as Unnormalized Key-Value Memories
Feed-forward layers
每个前馈层是一个 position-wise 的函数,独立地处理每个输入向量。设 $\mathbf{x} \in \mathbb{R}^d$ 对应输入文本前缀的向量。我们可以将前馈层 $FF(⋅)$ 表示为如下形式(省略了偏置项):
\[\text{FF}(\mathbf{x}) = f(\mathbf{x}·K^\top)·V \tag{1}\]其中 $K, V \in \mathbb{R}^{d_m \times d}$ 是参数矩阵,$f$ 是一个非线性函数,例如 ReLU。
Neural memory
一个神经记忆由 $d_m$ 个键值对组成,我们称之为记忆。每个键由一个 $d$ 维向量 $\mathbf{k}_i \in \mathbb{R}^d$ 表示,并共同形成参数矩阵 $K \in \mathbb{R}^{d_m \times d}$;类似地,我们将值参数定义为 $V \in \mathbb{R}^{d_m \times d}$。给定一个输入向量 $\mathbf{x} \in \mathbb{R}^d$ ,我们计算键上的分布,并用它来计算期望值:
\[p(k_i|x) \propto \exp(\mathbf{x}\cdot \mathbf{k}_i) \\ \text{MN}(\mathbf{x}) = \sum_{i=1}^{d_m} p(k_i|x)\mathbf{v}_i\]使用矩阵表示法,我们得到了一个更简洁的公式:
\[\text{MN}(\mathbf{x}) = \text{softmax}(\mathbf{x}\cdot K^\top)\cdot V \tag{2}\]Feed-forward layers emulate neural memory
比较方程 1 和方程 2 可以看出,前馈层与键值神经记忆几乎相同;唯一的区别是神经记忆使用 softmax 作为非线性函数 $f(⋅)$,而标准的 Transformer 在前馈层中不使用归一化函数。隐藏维度 $d_m$ 本质上是层中的记忆数量,激活 $\mathbf{m}=f(\mathbf{x}⋅K^\top) $ 通常称为隐藏层,是一个由每个记忆的未归一化非负系数组成的向量。我们将每个 $\mathbf{m}_i$ 称为第 $i$ 个记忆单元的记忆系数。
我们推测每个键向量 $\mathbf{k}_i$ 捕捉了输入序列中的特定模式(或一组模式),而其相应的值向量 $\mathbf{v}_i$ 表示了跟随该模式的标记分布。
Keys Capture Input Patterns
我们假设前馈层中的键向量 $K$ 充当输入序列的模式检测器,其中每个单独的键向量 $\mathbf{k}_i$ 对应于输入前缀 $x_1,…,x_j$ 上的特定模式。为了验证我们的假设,我们分析了经过训练的语言模型前馈层的键。我们首先获取与给定键最相关的训练示例(句子的前缀),即记忆系数最高的输入文本。然后,我们请人类在获取的示例中识别模式。对于样本中的几乎每个键 $\mathbf{k}_i$,都有一小组明确定义的模式被人类识别出来,覆盖了与该键相关的大部分示例。
Experiment
Retrieving trigger examples
我们假设存储在记忆单元中的模式源自模型训练时的样本。因此,给定与第 $\ell$ 层前馈层的第 $i$ 个隐藏维度对应的键 $\mathbf{k}^\ell_i$,我们为 WikiText-103 训练集中每个句子的每个前缀 $x_1, \ldots, x_j$ 计算记忆系数 $\text{ReLU}(\mathbf{x}^\ell_j \cdot \mathbf{k}^\ell_i)$。例如,对于假设的句子“I love dogs”,我们将计算三个系数,分别对应前缀“I”、“I love”和“I love dogs”。然后,我们检索出 top-t trigger examples,即在第 $\ell$ 层中与 $\mathbf{k}^\ell_i$ 的内积最高的 t 个前缀。
Pattern analysis
我们让人类专家对每个键检索出的前 25 个前缀进行标注,并要求他们:
- 识别至少在 3 个前缀中出现的重复模式(这将强烈表明与该键的关联,因为如果句子是随机抽取的,这种情况不太可能发生)
- 描述每个识别出的模式
- 将每个识别出的模式分类为“浅层”(例如,重复出现的 n-gram)或“语义”(重复出现的主题)
Results
Memories are associated with human recognizable patterns
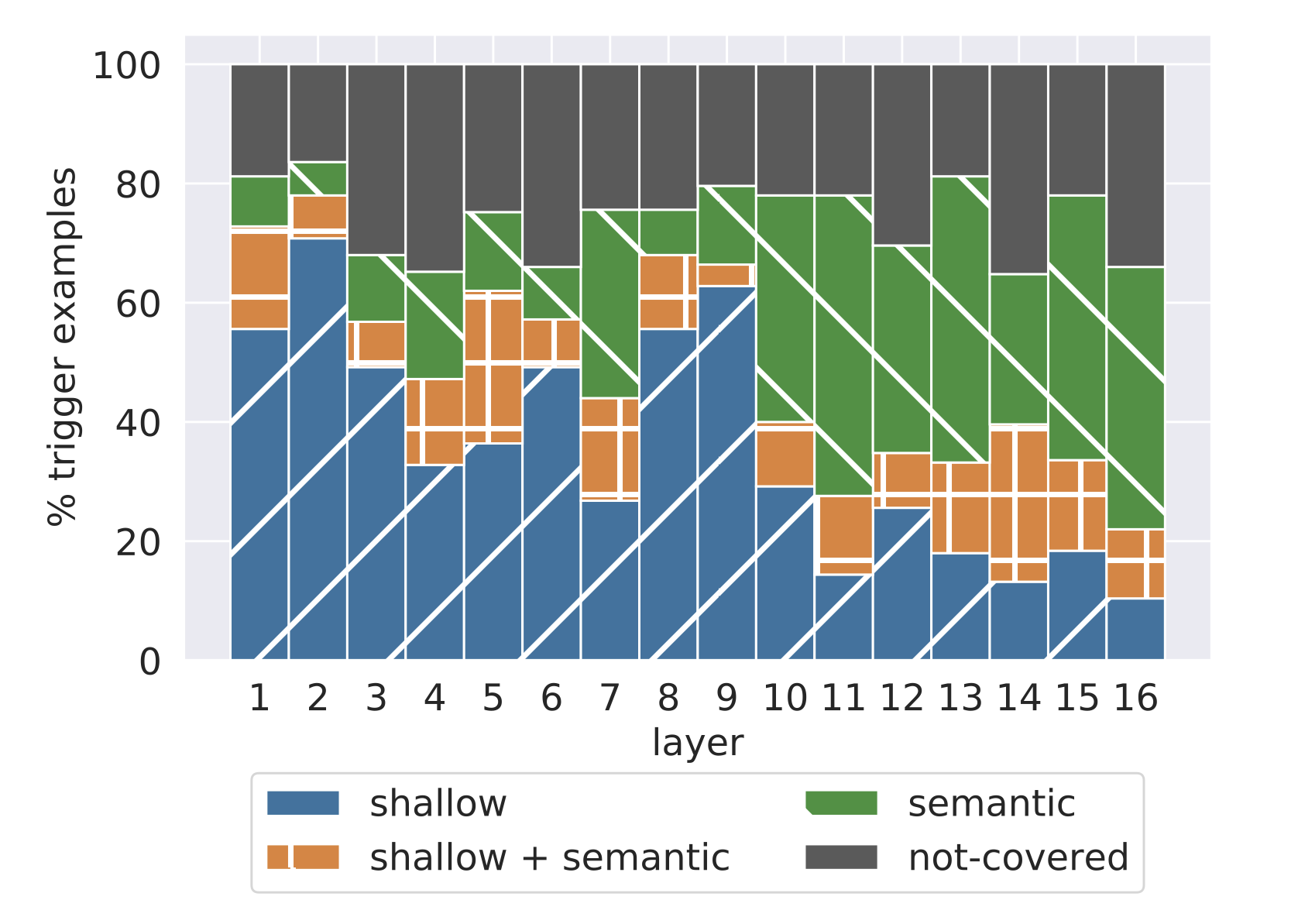
专家能够为每个键识别出至少一个模式,平均每个键识别出 3.6 个模式。此外,绝大多数检索到的前缀(65%-80%)与至少一个识别出的模式相关联(见图 2)。
Shallow layers detect shallow patterns
比较与浅层模式和语义模式相关联的前缀数量(见图 2),较低层(第 1-9 层)主要由浅层模式主导,通常这些前缀共享最后一个单词。相比之下,较高层(第 10-16 层)则以更多的语义模式为特征,前缀来自相似的上下文,但没有明显的表面形式相似性。这一观察结果支持了最近的发现,即深度上下文模型中的较低层(较高层)编码输入的浅层(语义)特征。
为了进一步验证这一假设,我们随机抽取了 1600 个键(每层 100 个键),并对每个键的前 50 个 trigger example 进行局部修改。具体来说,我们从输入中移除第一个、最后一个或一个随机的 token,并测量这种变动对记忆系数的影响。图 3 显示,模型认为示例的结尾比开头对预测下一个 token 更为重要。在较高层中,移除最后一个 token 的影响较小,这支持了我们的结论,即较高层的键与浅层模式的相关性较低。
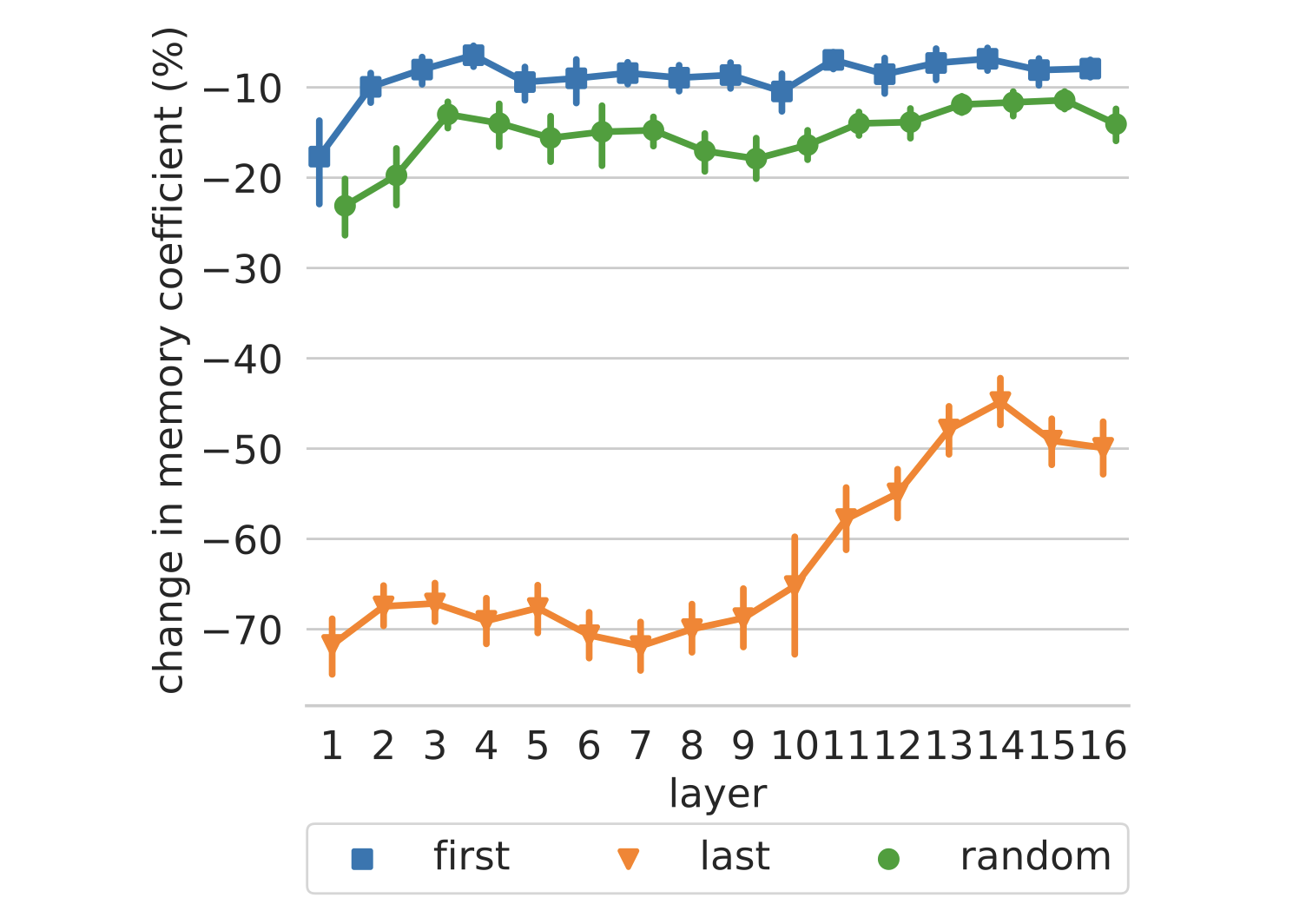
图 3:从输入中删除第一个、最后一个或随机一个标记而引起的记忆系数的相对变化。
Values Represent Distributions
我们展示了每个值 $\mathbf{v}^\ell_i$ 可以被视为输出词汇表的分布,并证明了这个分布补充了模型上层中对应键 $\mathbf{k}^\ell_i$ 的模式(见图 1)。
Casting values as distributions over the vocabulary
我们首先通过将每个值向量 $\mathbf{v}^\ell_i$ 乘以输出嵌入矩阵 $E$ 并应用 softmax,将其转换为词汇表上的概率分布:
\[\mathbf{p}^\ell_i=\text{softmax}(\mathbf{v}^\ell_i \cdot E)\]概率分布 $\mathbf{p}^\ell_i$ 是未校准的,因为值向量 $\mathbf{v}^\ell_i$ 通常会乘以与输入相关的记忆系数 $\mathbf{m}^\ell_i$,这会改变输出分布的偏度(skewness)。尽管如此,由 $\mathbf{p}^\ell_i$ 引入的排序对系数来说是不变的(排序与系数无关)。这个转换假设模型的所有层都在相同的嵌入空间中操作。
Value predictions follow key patterns in upper layers
对于每一层 $\ell$ 和记忆维度 $i$,我们根据 $\mathbf{v}^\ell_i$ 的最高排名 token($\text{argmax}(\mathbf{p}^\ell_i)$)与根据 $\mathbf{k}^\ell_i$ 的 top-1 trigger example 中的下一个 token $w^\ell_i$ 进行比较。图 4 显示了一致率,即值的最高预测与键的 top trigger example 匹配的记忆单元(维度)比例($\text{argmax}(\mathbf{p}^\ell_i) = w^\ell_i$)。可以看出,在较低层(1-10 层)中一致率接近于零,但从第 11 层开始,一致率迅速上升至 3.5%,显示出键和值在 top-ranked token 的更高一致性。重要的是,这个值比从词汇表中随机预测 token 的数量级高得多,随机预测会产生远低得多的一致率(0.0004%),这表明上层记忆表现出非平凡的预测能力。
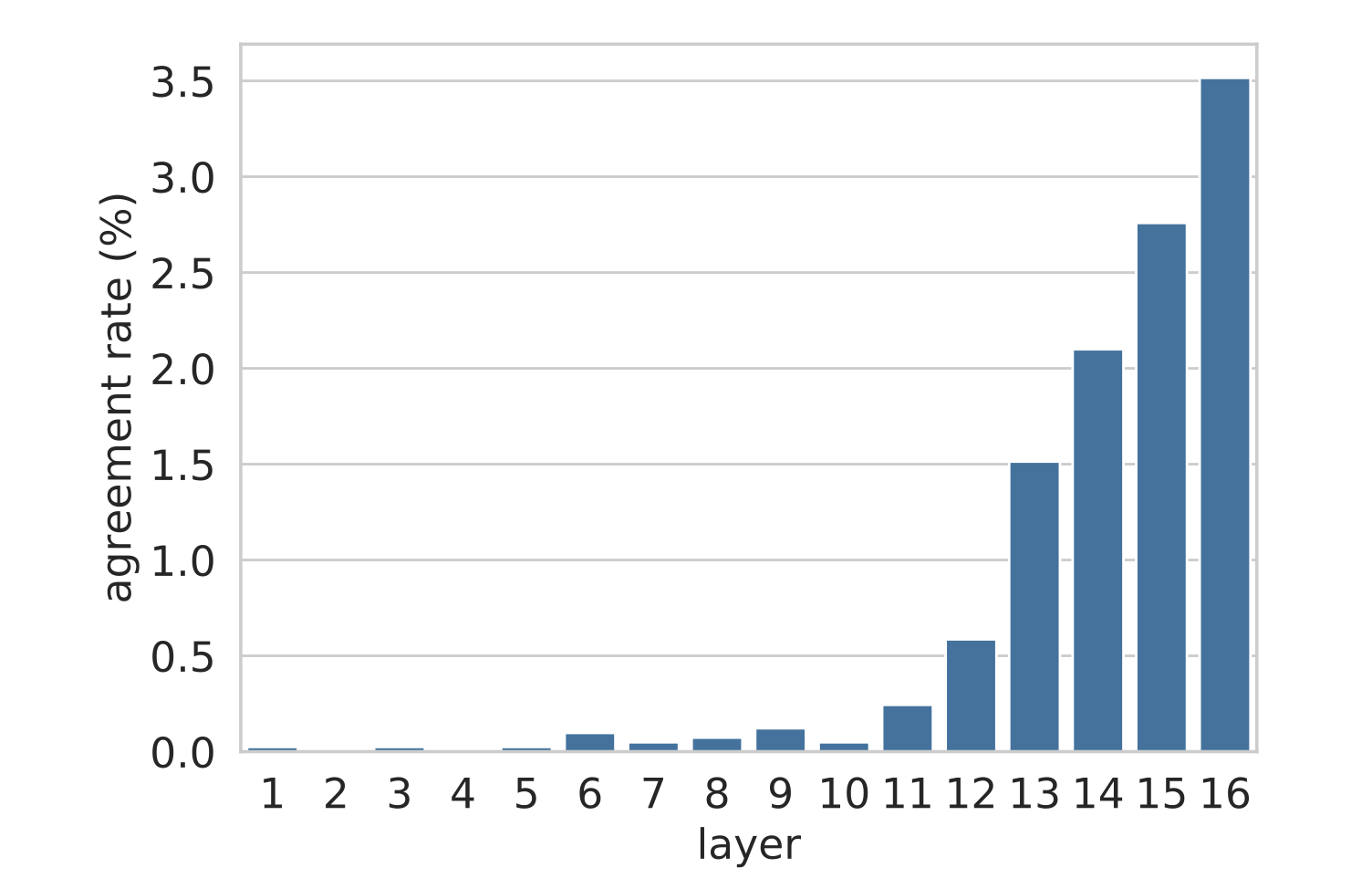
图 4:基于值向量 $\mathbf{v}^\ell_i$ 的排名靠前的 token 与与键向量相关联的排名靠前的 trigger example 的下一个 token 之间的一致率。
接下来,我们取 $\mathbf{k}^\ell_i$ 的 top-1 trigger example 的下一个 token($w^\ell_i$),并找出它在值向量分布 $\mathbf{p}^\ell_i$ 中的排名。结果显示,trigger example 的下一个 token 的排名随着层数的增加而提高,这意味着 $w^\ell_i$ 在较高层中往往获得更高的概率。
Detecting predictive values
我们分析了值的最高预测概率,即 $\text{max}(\mathbf{p}^\ell_i)$。结果显示,尽管这些分布未校准,但具有较高最大概率的分布更可能与其键的 top trigger example 一致。然后,我们选取所有层和维度中概率最高的 100 个值(其中 97 个在上层,11-16 层),并对每个值 $\mathbf{v}^\ell_i$ 分析 $\mathbf{k}^\ell_i$ 的前 50 个 trigger example。我们发现,在几乎一半的值中(100 个中的 46 个),至少有一个 trigger example 与该值的最高预测一致。
Discussion
当被视为输出词汇表上的分布时,上层的值往往会为触发相应键的示例的下一个 token 分配更高的概率。这表明上层的记忆单元通常存储了如何直接从输入(前缀中的模式)预测输出(下一个单词的分布)的信息。相反,较低层没有表现出键模式与相应值分布之间的这种明显相关性。一个可能的解释是,较低层不在相同的嵌入空间中操作,因此,使用输出嵌入将值投影到词汇表上并不会产生遵循 trigger example 的分布。
Aggregating Memories
到目前为止,我们的讨论集中在前馈层中单个记忆单元的功能。那么,来自多个层中多个单元的信息是如何聚合成一个模型范围的预测的呢?我们展示了每个前馈层结合了多个记忆,以产生与其各个组成记忆的值分布显著不同的分布。这些逐层的分布通过残差连接进行组合,每个前馈层更新残差的分布,最终形成模型的输出。
Intra-Layer Memory Composition
前馈层的输出可以定义为值向量按其记忆系数的加权求和,再加上一个偏置项:
\[\mathbf{y}^\ell = \sum_i \text{ReLU}(\mathbf{x}^\ell \cdot \mathbf{k}^\ell_i) \cdot \mathbf{v}^\ell_i + \mathbf{b}^\ell\]如果每个值向量 $\mathbf{v}^\ell_i$ 包含关于目标 token 分布的信息,这些信息是如何聚合成一个单一的输出分布的呢?为了找出答案,我们分析了验证集中随机抽取的 4000 个前缀。在这里,使用验证集是为了试图描述模型在推理时的行为,而不是寻找它在训练期间“记住”的示例。
我们首先测量“活跃”记忆(系数非零的单元)的比例。图 7 显示,一个典型的示例在每层触发数百个记忆(占 4096 个维度的 10%-50%),但大多数单元仍然不活跃。有趣的是,活跃记忆的数量在第 10 层下降,而根据图 2,这一层也是语义模式比浅层模式更普遍的层。
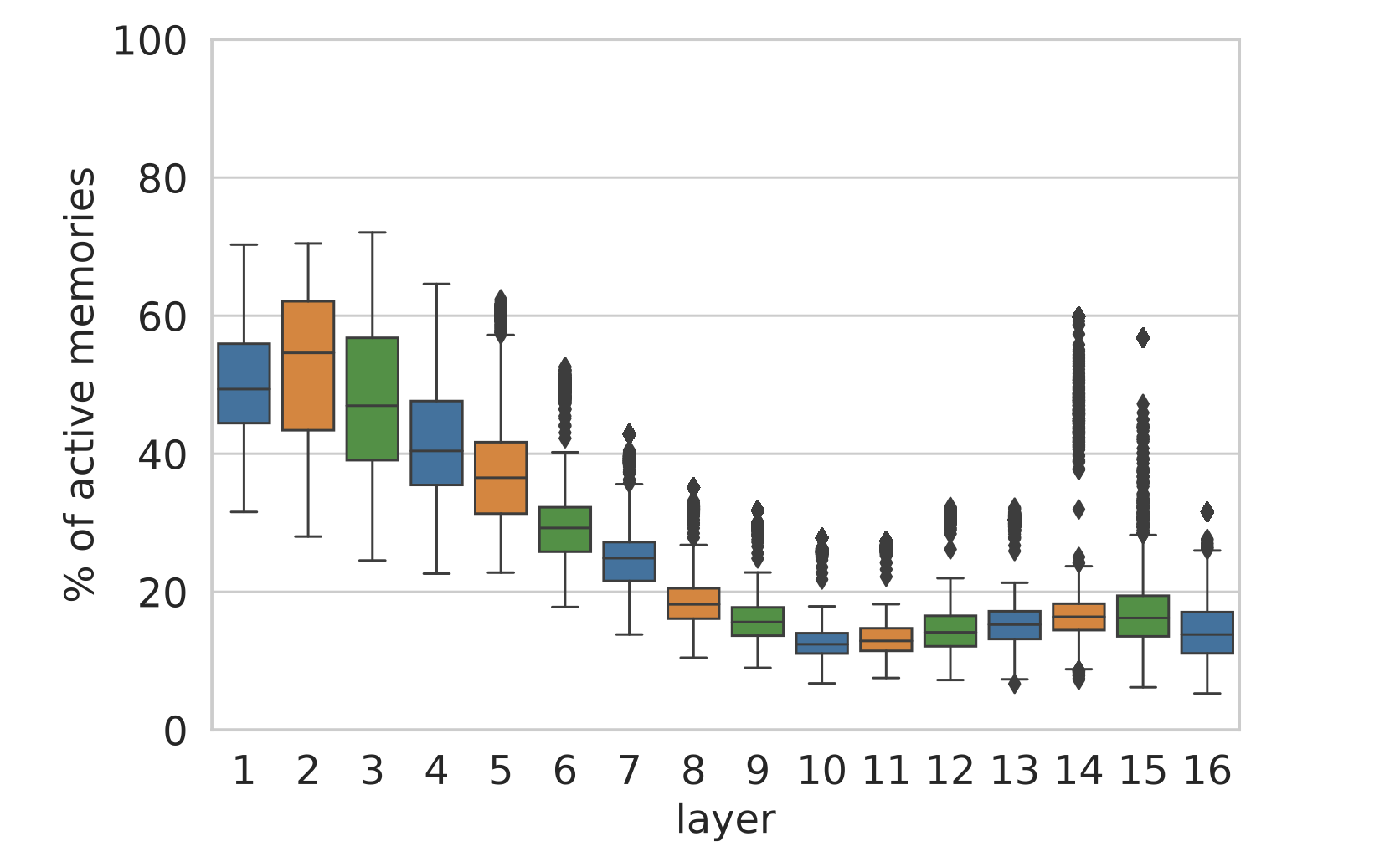
图 7:对于 4,000 个随机样本,每个层中 4096 个记忆中的活跃记忆(即具有正的记忆系数)的比例。
虽然有些情况下单个记忆单元主导了层的输出,但大多数输出是组合性的。我们统计了前馈层的最高预测与所有记忆的最高预测不同的数量。形式上,我们表示为:
\[\text{top}(\mathbf{h}) = \text{argmax}(\mathbf{h} \cdot E)\]作为由向量 $\mathbf{h}$ 引发的词汇分布中最高预测的通用简写,并计算满足以下条件的样本数量:
\[\forall i : \text{top}(\mathbf{v}^\ell_i) \neq \text{top}(\mathbf{y}^\ell)\]图 8 显示,对于网络中的任何一层,该层的最终预测在至少约 68% 的样本中与每个记忆的预测不同。即使在上层,记忆的值与输出空间的相关性更高,层级预测通常也不是单个主导记忆单元的结果,而是多个记忆的组合。
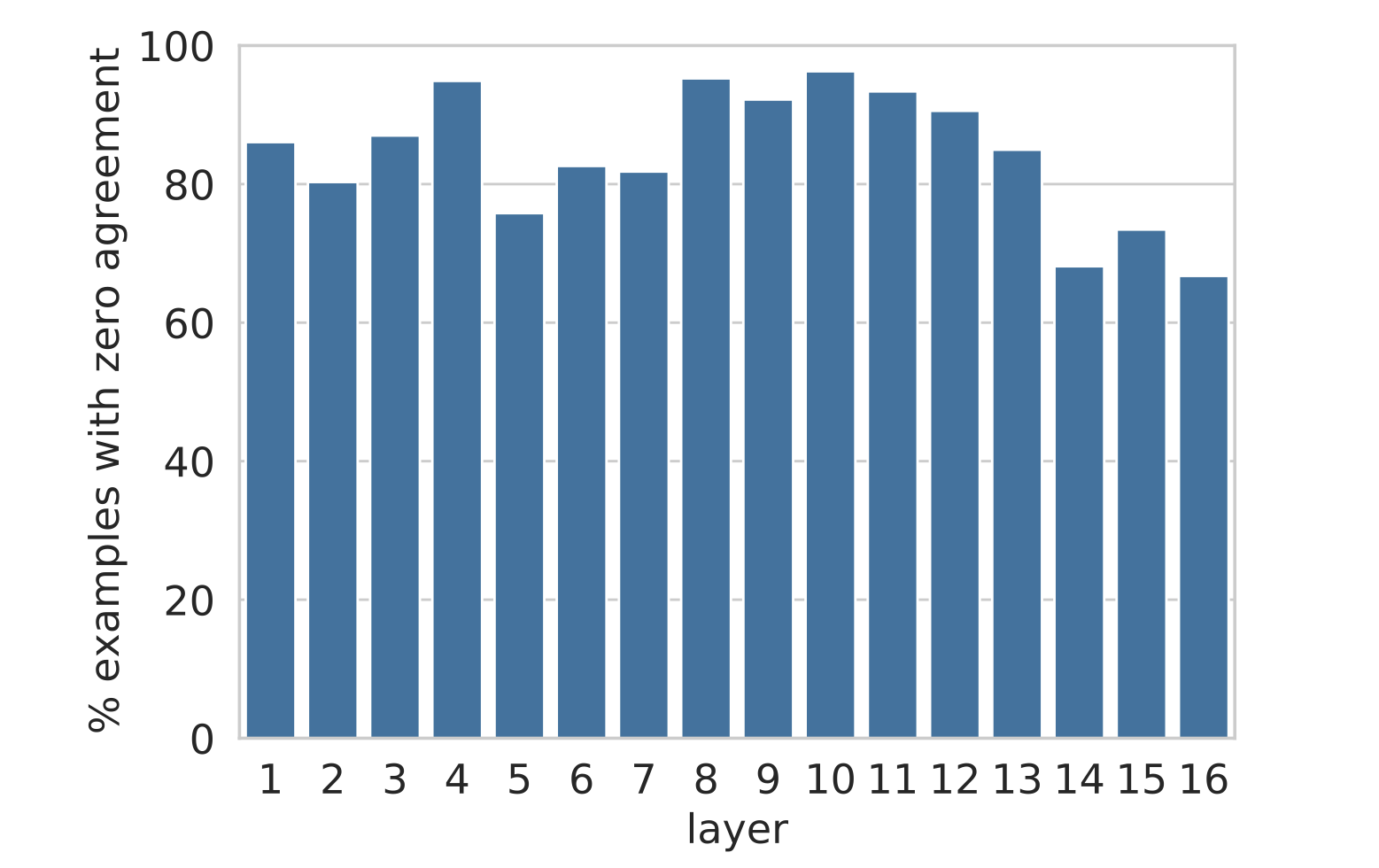
图 8:在 4,000 个随机样本中,层的预测与其所有记忆的预测不同的示例比例。
我们进一步分析了至少有一个记忆单元与层的预测一致的情况,发现 (a) 在 60% 的示例中,目标 token 是词汇表中的常见停用词(例如 “the” 或 “of”);(b) 在 43% 的情况下,输入前缀少于 5 个 token。这表明训练数据中非常常见的模式可能被“缓存”在单个记忆单元中,并且不需要组合性。
Inter-Layer Prediction Refinement
虽然单个前馈层是并行组合其记忆的,但多层模型使用残差连接 $\mathbf{r}$ 来顺序组合预测,以生成模型的最终输出:
\[\begin{aligned} \mathbf{x}^\ell &= \text{LayerNorm}(\mathbf{r}^\ell) \\ \mathbf{y}^\ell &= \text{FF}(\mathbf{x}^\ell) \\ \mathbf{o}^\ell &= \mathbf{y}^\ell + \mathbf{r}^\ell \\ \end{aligned}\]我们假设模型使用顺序组合装置(sequential composition apparatus)作为一种手段,从一层到另一层逐步精细化其预测,通常在较低层决定预测结果。
为了验证我们的假设,我们首先测量由残差向量 $\mathbf{r}^\ell$ 引发的概率分布与模型最终输出 $\mathbf{o}^L$($L$ 为总层数)的匹配程度:
\[\text{top}(\mathbf{r}^\ell) = \text{top}(\mathbf{o}^L)\]图 9 显示,大约三分之一的模型预测是在底部的几层中确定的。从第 10 层开始,这个数字迅速增长,这意味着大多数“困难”决策在最后一层之前就已经做出。
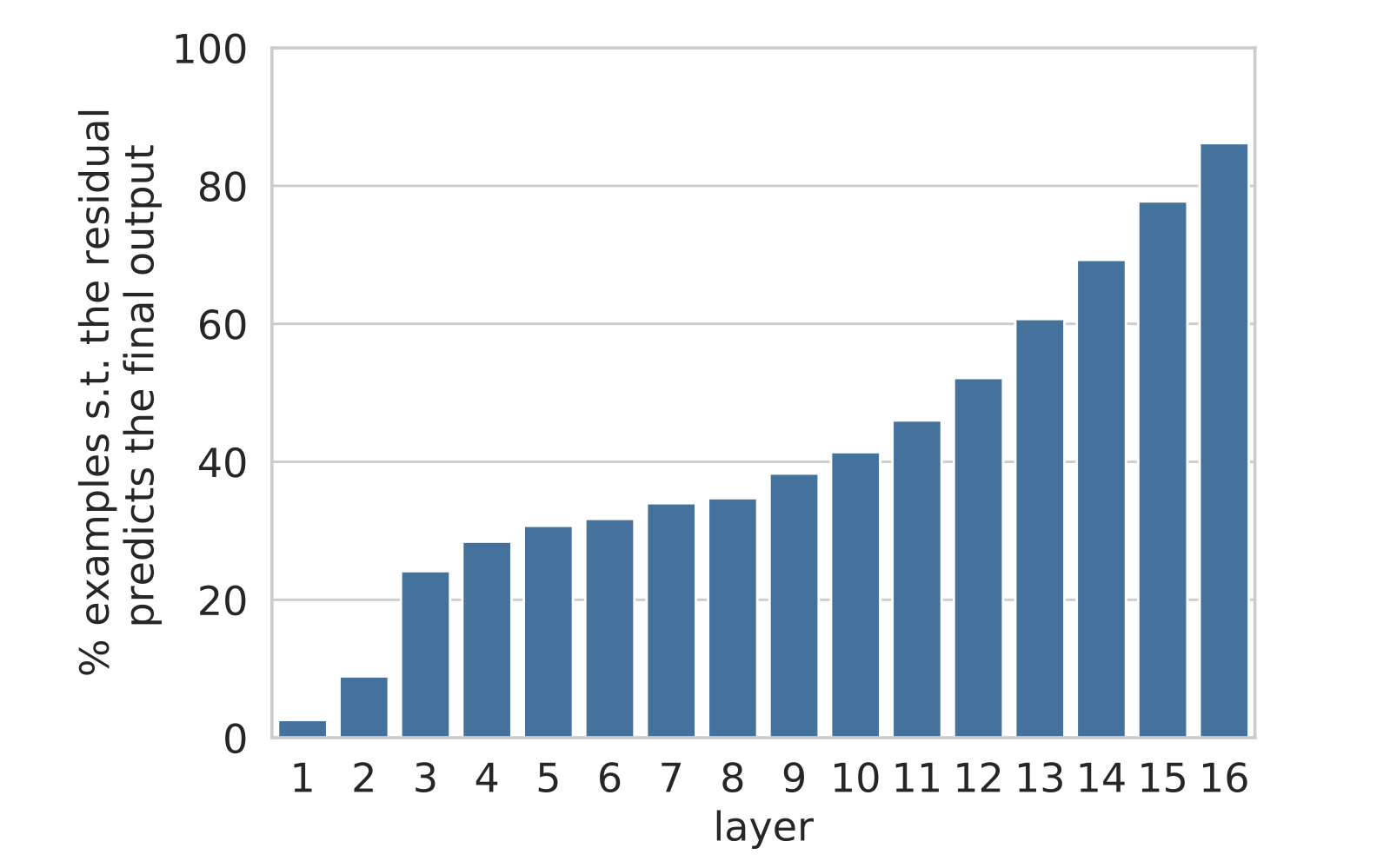
图 9:每个层中残差的 top 预测与模型的输出匹配的比例
我们还测量了每一层的残差向量 $\mathbf{r}^\ell$ 分配给模型最终预测的概率质量 $p$:
\[\begin{aligned} w &= \text{top}(\mathbf{o}^L) \\ \mathbf{p} &= \text{softmax}(\mathbf{r}^\ell \cdot E) \\ p &= \mathbf{p}_w \end{aligned}\]图 10 显示了类似的趋势,随着在层中逐步推进,不仅是最高预测的标识得到了优化,模型对其决策的信心也在增强。
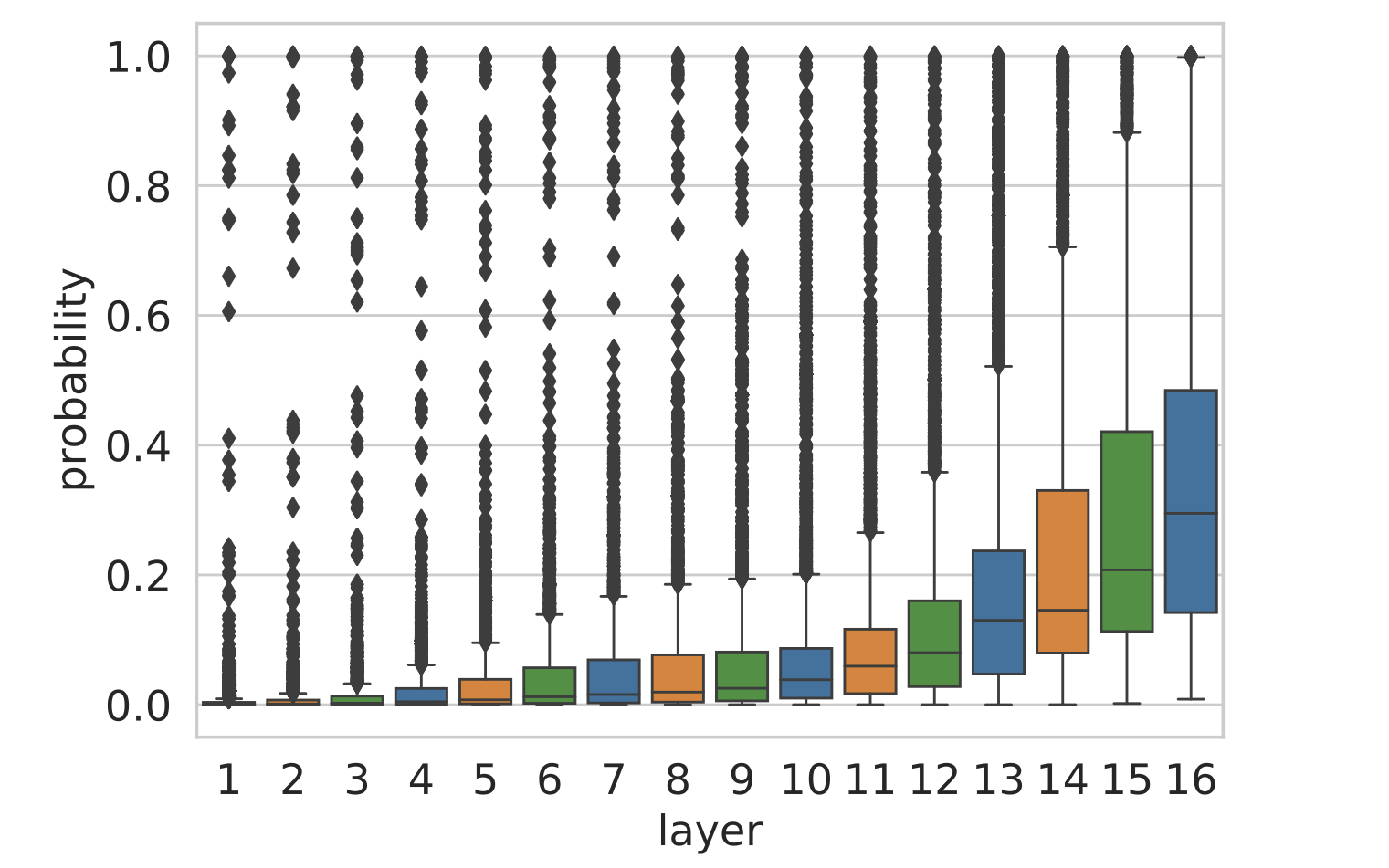
图 10:根据每个层的残差,模型输出的 token 的概率
为了更好地理解每一层的精细化过程如何运作,我们测量了残差的 top 预测在与前馈层交互后发生变化的频率($\text{top}(\mathbf{r}^\ell) \neq \text{top}(\mathbf{o}^\ell)$),以及这种变化是由于前馈层覆盖了残差($\text{top}(\mathbf{o}^\ell) = \text{top}(\mathbf{y}^\ell)$)还是由于真正的组合($\text{top}(\mathbf{r}^\ell) \neq \text{top}(\mathbf{o}^\ell) \neq \text{top}(\mathbf{y}^\ell)$)导致的。
图 11 显示了每层不同情况的细分。在绝大多数示例中,残差的 top 预测最终成为模型的预测(residual + agreement),其中大多数前馈层的预测和模型预测不同(residual)。令人惊讶的是,当残差的预测确实发生变化时(composition+ffn),它很少变为前馈层的预测(ffn)。相反,我们观察到将残差的分布与前馈层的分布组合会产生一个“折中(compromise)”预测,这与两者都不相同(composition)。一个可能的猜测是,前馈层充当了一种消除机制,以“否决”残差中的 top 预测,从而将概率质量转移到残差分布头部的其他候选预测之一。
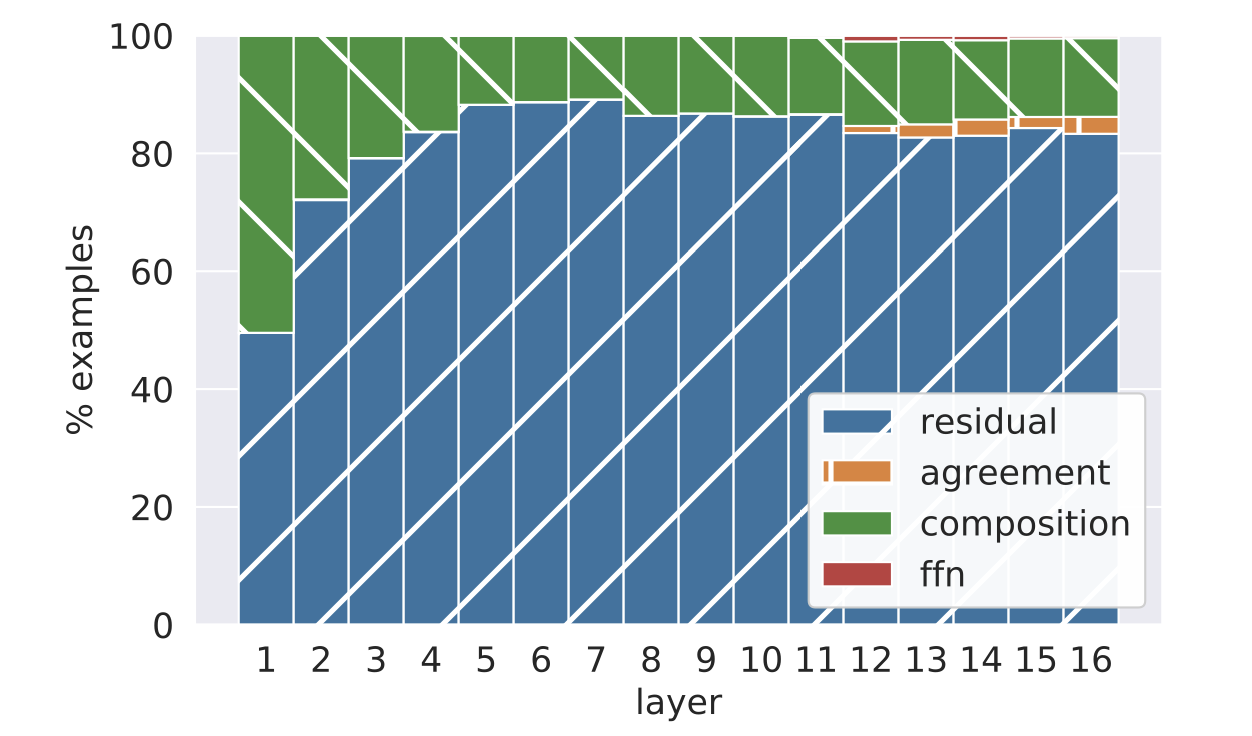
图11:按照预测情况细分的示例:层的输出预测与残差的预测相匹配(residual),与前馈层的预测相匹配(ffn),与两者的预测都相匹配(agreement),或者两者的预测都不匹配(composition)。
最后,我们手动分析了最后一层组合(前馈层在最后一层修改了残差输出)的 100 个随机案例。我们发现,在大多数情况下(66 个例子),输出会变为一个语义上相距较远的词(例如,“people” → “same”),而在其余情况下(34 个例子),前馈层的输出将残差预测调整为一个相关的词(例如,“later” → “earlier” 和 “gastric” → “stomach”)。这表明前馈层在不同的粒度上对残差预测进行调整,即使在模型的最后一层也是如此。
Discussion and Conclusion
在这项工作中,我们提出前馈层模拟键值记忆,并提供了一系列实验表明:
- 键与人类可解释的输入模式相关联
- 大部分位于模型上层的值,会引导模型输出与相应键中模式的下一个 token 分布相关的词汇分布
- 模型的输出是通过这些分布的聚合形成的,它们首先被组合形成各个层的输出,然后通过残差连接在模型的各层中进行精细化