本文为课程 Stanford CS336 - Language Modeling from Scratch 的笔记。
Tokenizer
- Character-based tokenization
- Byte-based tokenization
- Word-based tokenization
- Byte Pair Encoding (BPE)
资料:
Transformer
The Transformer Model in Equations
Transformer 将 $\mathbb{R}^d$ 空间中的 $n$ 个对象集合转换为$\mathbb{R}^d$ 空间中另一组数量为 $n$ 的对象集合。需要注意,这是对对象集合的变换,而非对序列的变换。Transformer 本质上不感知 $n$ 个输入元素之间的任何结构关系——无论是顺序结构还是其他结构。
我们可以用 Transformer $f_\theta(x) \in \mathbb{R}^{n \times d}$ 来参数化 $z$。虽然 Transformer 的输出是 $n \times d$ 维的,但通常只使用单个输出 $z \equiv f_\theta(x)_n \in \mathbb{R}^d$,依靠端到端训练将相关信息集中在变换数据的第 $n$ 个元素中。这种做法与使用循环神经网络或 LSTM 模型的最终潜在状态作为表示的常见做法大致类似,可能是受到了后者的启发。
与循环神经网络或卷积模型类似,Transformer 通过控制参数化函数类的表达能力来缓解过拟合问题。从参数数量的角度来看,全连接网络中的参数数量与输入 $x$ 的维度呈线性关系,但与输入数量 $n$ 无关。
关于 Transformer 的注意力权重与 LSTM 权重之间的类比,请参见 Levy 等人 Long short-term memory as a dynamically computed element-wise weighted sum 的第 4 节。简单的说, Transformer 是对称性的,LSTM 是不对称性的。另一种理解方式是,LSTM 本质上是因果的:如果你想要双向上下文,你需要用例如 bi-lstm 来增强它。相比之下,Transformer 是非因果的,其输入必须被掩码才能应用于语言建模等序列学习任务。此外,在 LSTM 中对先前元素的注意力是单调递减的,而 Transformer 可以同等地关注集合中所有元素。
The Illustrated GPT-2
FLOPs
The FLOPs Calculus of Language Model Training
What’s the Backward-Forward FLOP Ratio for Neural Networks?
Architecture Variations
Pre Norm vs Post Norm
几乎所有现代语言模型都使用 pre norm。
LayerNorm vs RMSNorm
许多现代语言模型使用 RMSNorm——不减去均值也不添加偏置项。
LayerNorm 公式:
\[\text{LayerNorm}(x) = \gamma \odot \frac{x - \mu}{\sigma} + \beta\]其中 $\mu$ 是均值,$\sigma$ 是标准差,$\gamma, \beta$ 是可学习的缩放和偏移参数。
RMSNorm 公式:
\[\text{RMSNorm}(x) = \gamma \odot \frac{x}{\sqrt{||x||^2_2 + \epsilon}}\]其中 $\gamma$ 是可学习的缩放参数。
现代解释——它更快(且效果同样好)
- 更少的操作(无需计算均值)
- 更少的参数(无需存储偏置项)
- 更少的数据移动(无需计算均值)
Dropping Bias Terms
大多数现代 Transformer 都没有偏置项。
Activations
GeLU (Gaussian Error Linear Unit)
\[\text{GeLU}(x) = x \cdot \Phi(x) = x \cdot \frac{1}{2}\left[1 + \text{erf}\left(\frac{x}{\sqrt{2}}\right)\right]\]其中 $\Phi(x)$ 是标准正态分布的累积分布函数。近似公式:
\[\text{GeLU}(x) \approx 0.5x\left(1 + \tanh\left(\sqrt{\frac{2}{\pi}}\left(x + 0.044715x^3\right)\right)\right)\]- 平滑性:比 ReLU 更平滑,没有硬截断
- 非单调性:在负值区域有小的负输出
- 可微分:处处可导,有利于梯度传播
- 性能:在语言模型中通常比 ReLU 表现更好
Gated Activations (*GLU)
GLU 修改了前馈层的第一部分。标准前馈层:
\[FF(x) = \max(0, xW_1)W_2\]在线性 + ReLU 上增加一个(逐元素)线性项:
\[\max(0, xW_1) \rightarrow \max(0, xW_1) \odot (xV)\]标准前馈层的门控变体:
ReGLU:
\[FF_{ReGLU}(x) = (\max(0, xW_1) \odot xV)W_2\]GeGLU:
\[FF_{GeGLU}(x) = (\text{GeLU}(xW_1) \odot xV)W_2\]SwiGLU:($\text{Swish}(x) = x \cdot \text{sigmoid}(x)$)
\[FF_{SwiGLU}(x) = (\text{Swish}(xW_1) \odot xV)W_2\]门控模型一般使用更小的 $d_{ff}$ 维度,约为原来的 2/3,以保持模型参数量一致。
Position Embeddings
Sine Positional Encoding
使用正/余弦函数来实现位置定位:
\[\text{Embed}(x, i) = v_x + PE_{pos}\]其中 $PE_{pos}$ 是位置编码:
\[\begin{aligned} PE_{(pos, 2i)} &= \sin(pos / 10000^{2i/d_{model}}) \\ PE_{(pos, 2i+1)} &= \cos(pos / 10000^{2i/d_{model}}) \end{aligned}\]代表模型: 原始 Transformer
Absolute Positional Embedding
在嵌入向量添加位置向量:
\[\text{Embed}(x, i) = v_x + u_i\]其中 $u_i$ 是可学习的位置嵌入向量。
代表模型: GPT-1/2/3, OPT
Relative Positional Embedding
在注意力计算添加位置向量:
\[e_{ij} = \frac{x_iW^Q(x_jW^K+a_{ij}^K)^\top}{\sqrt{d_z}}\]代表模型: T5, Gopher, Chinchilla
RoPE (Rotary Position Embedding)
核心思想
相对位置嵌入函数 $f(x, i)$ 应该满足 $\langle f(x,i), f(y,j)\rangle = g(x,y,i-j)$。即嵌入向量内积后只依赖于相对位置 $(i-j)$。
现有嵌入方式的问题
-
正弦位置编码: 包含各种非相对位置的交叉项(如 $\langle PE_i, v_y \rangle$):
\[\langle \text{Embed}(x, i), \text{Embed}(y, j) \rangle = \langle v_x, v_y \rangle + \langle PE_i, v_y \rangle + \ldots\] -
绝对位置编码: 显然不是相对的
-
相对位置编码: 不是内积形式
如何解决这个问题?
- 嵌入向量应该对绝对位置保持不变性
- 内积对任意旋转变换保持不变性
RoPE 解决方案
通过旋转变换将位置信息编码到查询和键向量中:
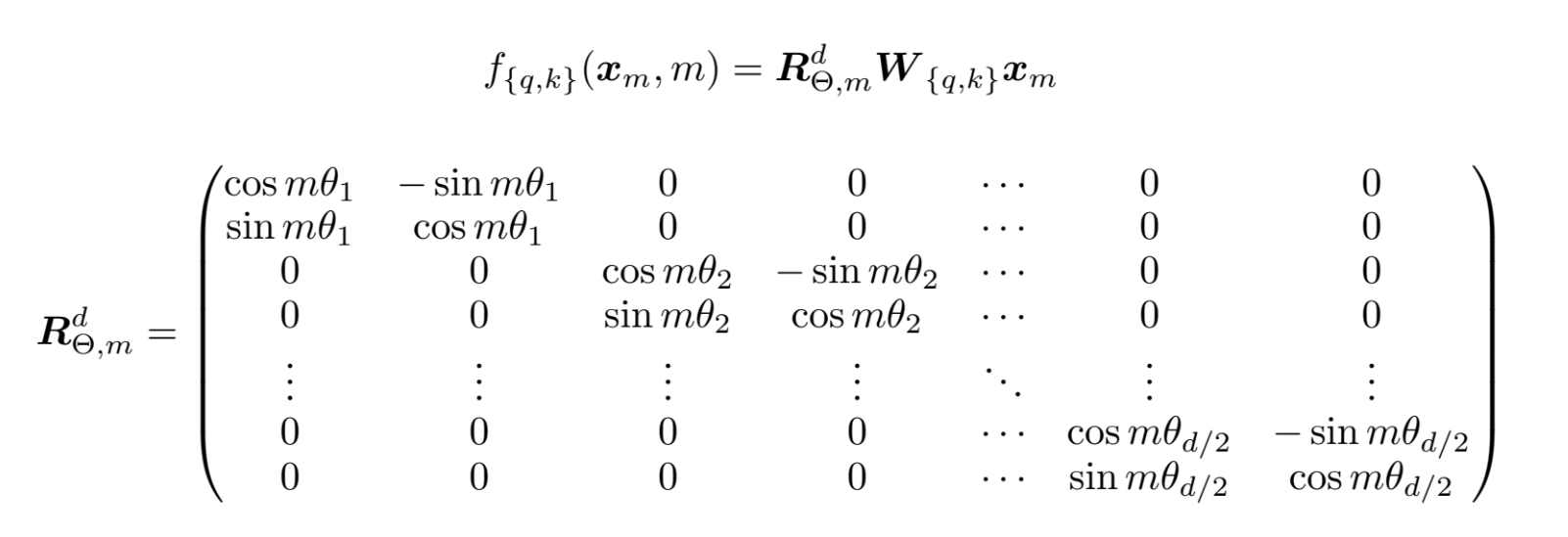
Hyperparameters
Feedforward – Model Dimension Ratio
\[d_{ff} = 4 d_{model}\]GLU 变体按 2/3 的比例缩放。这意味着大多数 GLU 变体都有:
\[d_{ff} = \frac{8}{3} d_{model}\]Head-Dim * Num-Heads to Model-Dim
大多数模型的比值都在 1 左右。
Aspect ratios
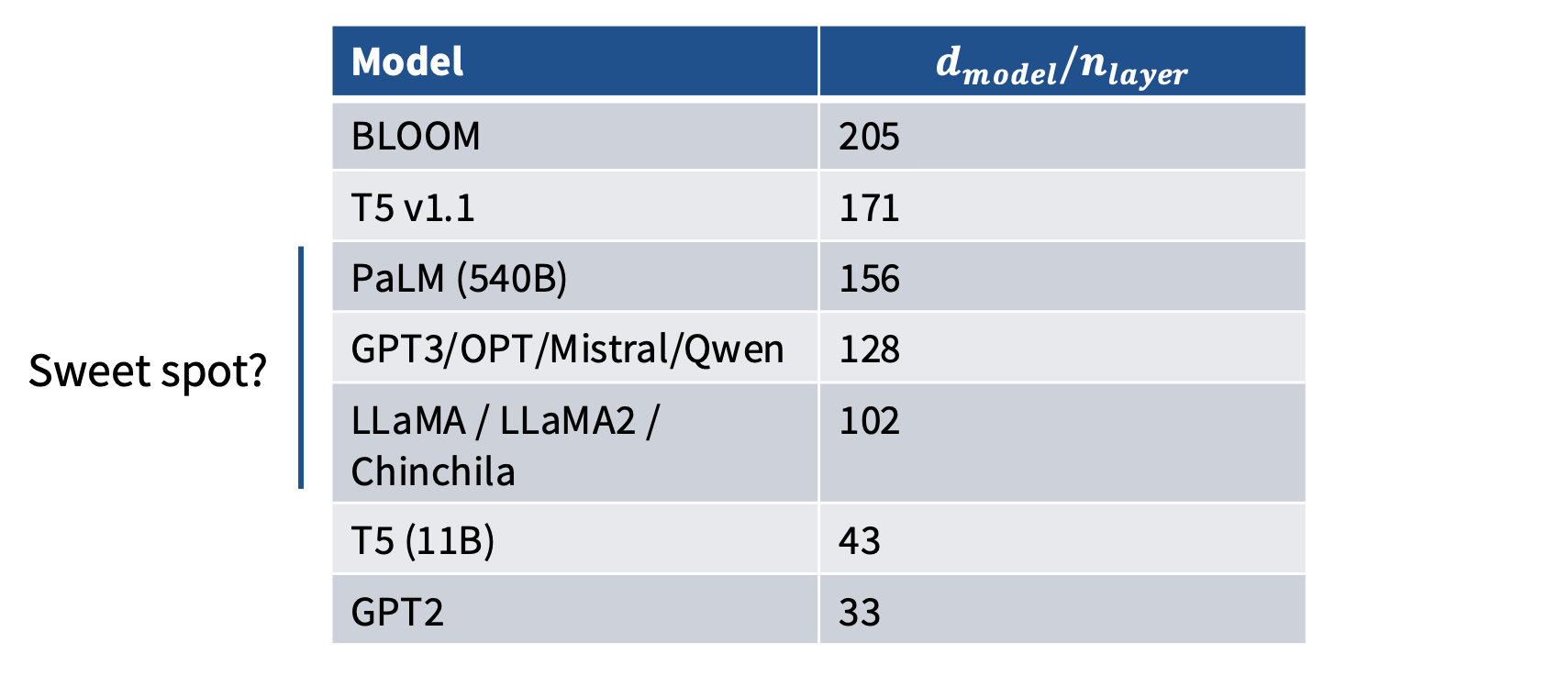
Vocabulary Sizes
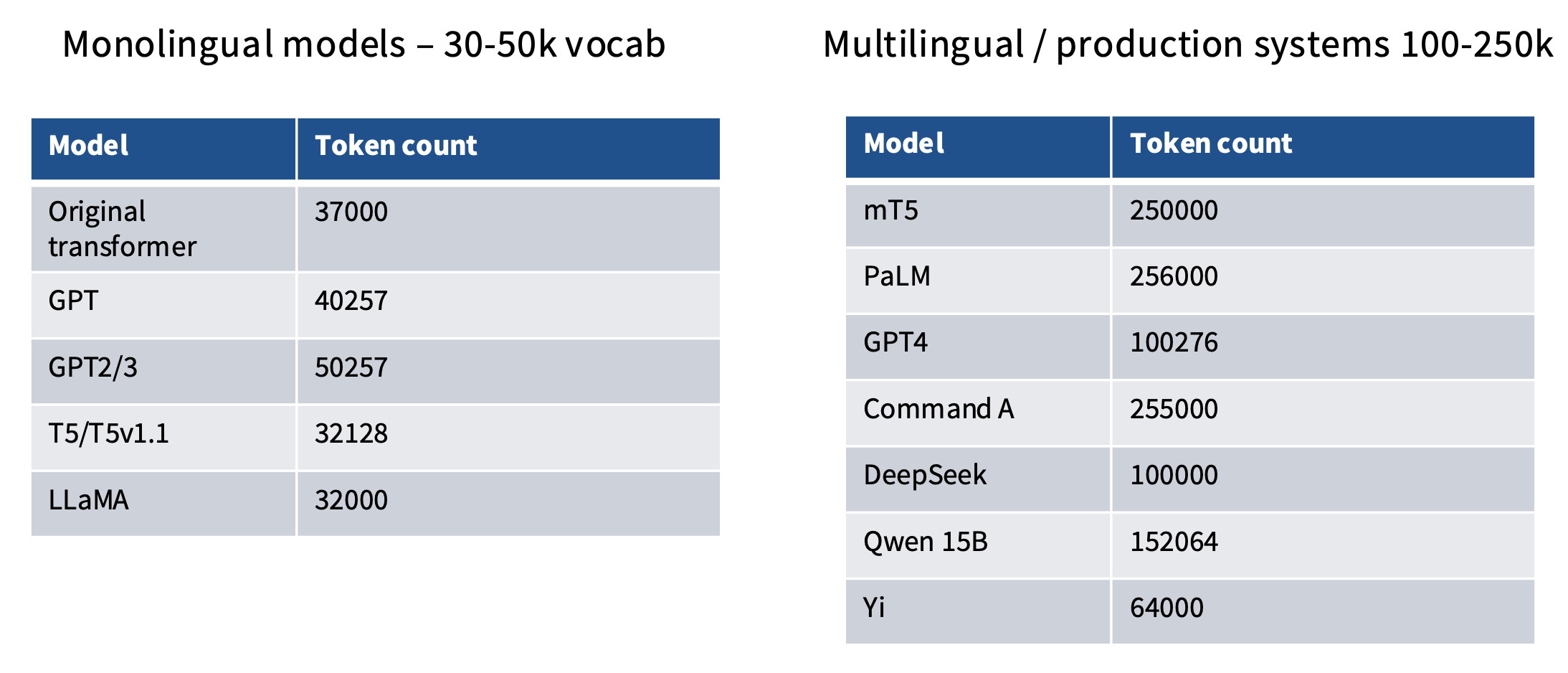
单语言词汇表不需要很大,但多语言词汇表需要比较大的词表。
Dropout and other regularization
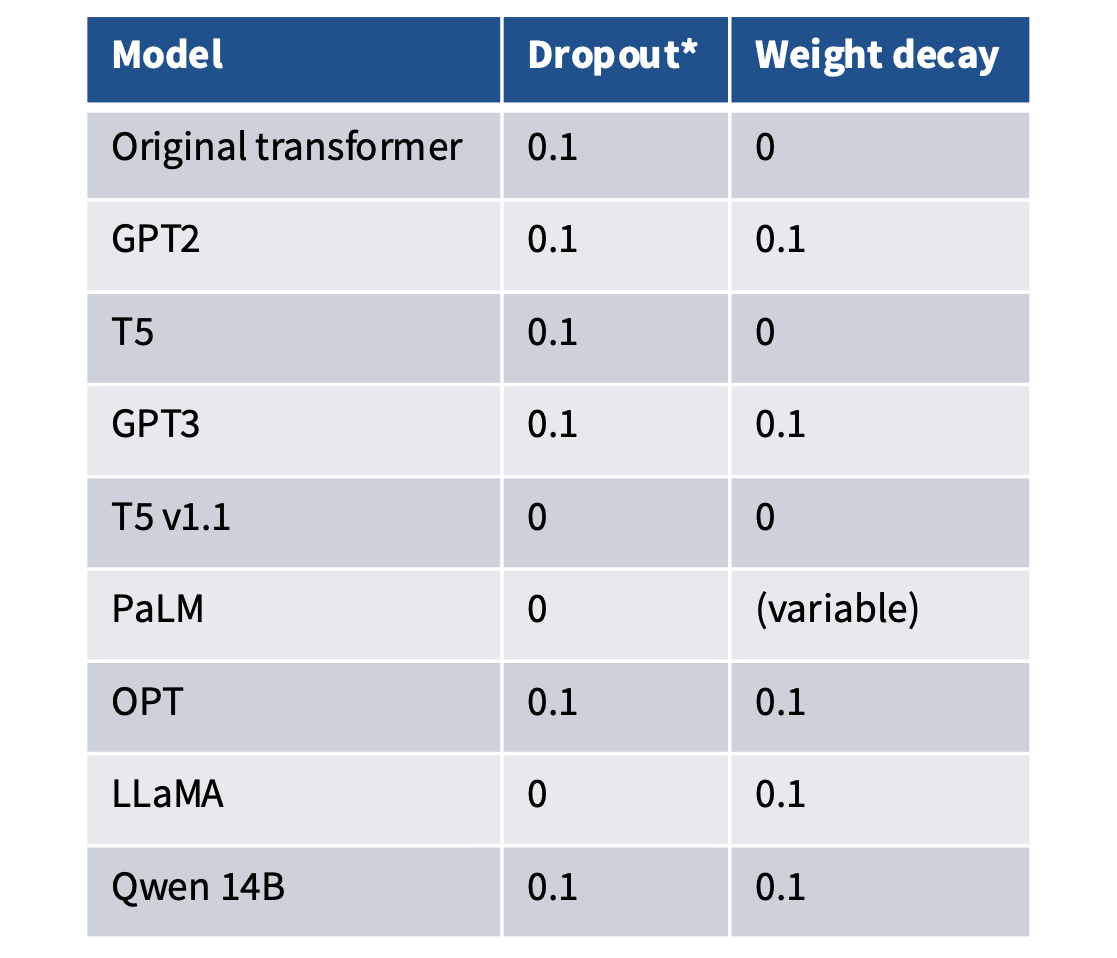
许多较老的模型在预训练期间使用 dropout。较新的模型(除了 Qwen)仅依赖 weight decay。
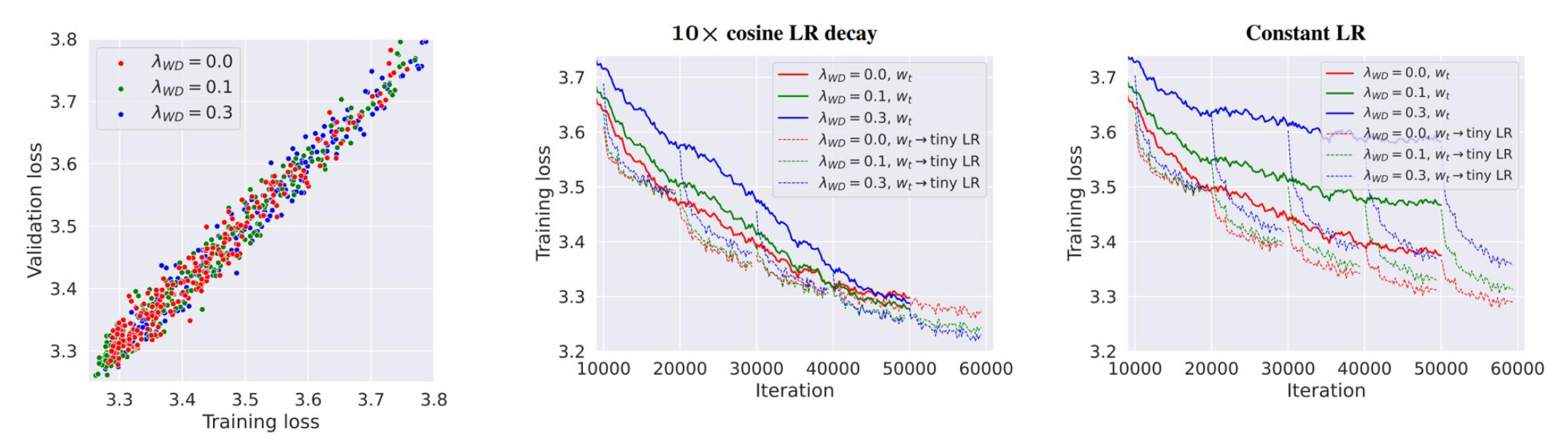
论文<Why Do We Need Weight Decay in Modern Deep Learning?> 对 LLM 权重衰减有有趣的观察:它不是用来控制过拟合的,而是与学习率(余弦调度)相互作用。
Stability Tricks
训练的不稳定训练性通常出自于 softmax——指数运算/除零。
Output softmax stability – the ‘z-loss’
标准 softmax:
\[\begin{aligned} \log(P(x)) &= \log \left(\frac{e^{U_r(x)}}{Z(x)}\right) \\ &= U_r(x) - \log(Z(x)) \\ Z(x) &= \sum_{r'=1}^{|V|}e^{U_{r'}(x)} \end{aligned}\]新增辅助 z-loss:
\[\begin{aligned} L &= \sum_i[\log(P(x_i)) - \alpha(\log(Z(x_i)) - 0)^2] \\ &= \sum_i[\log(P(x_i)) - \alpha\log^2(Z(x_i))] \end{aligned}\]Palm 中提到:“我们额外使用一个辅助损失函数 z loss = 10⁻⁴ · log² Z,以鼓励 softmax 归一化因子 log(Z) 接近 0,我们发现这能提高训练的稳定性。”
Attention softmax stability – the ‘QK norm’
Baseline 版本的 Transformer 块:
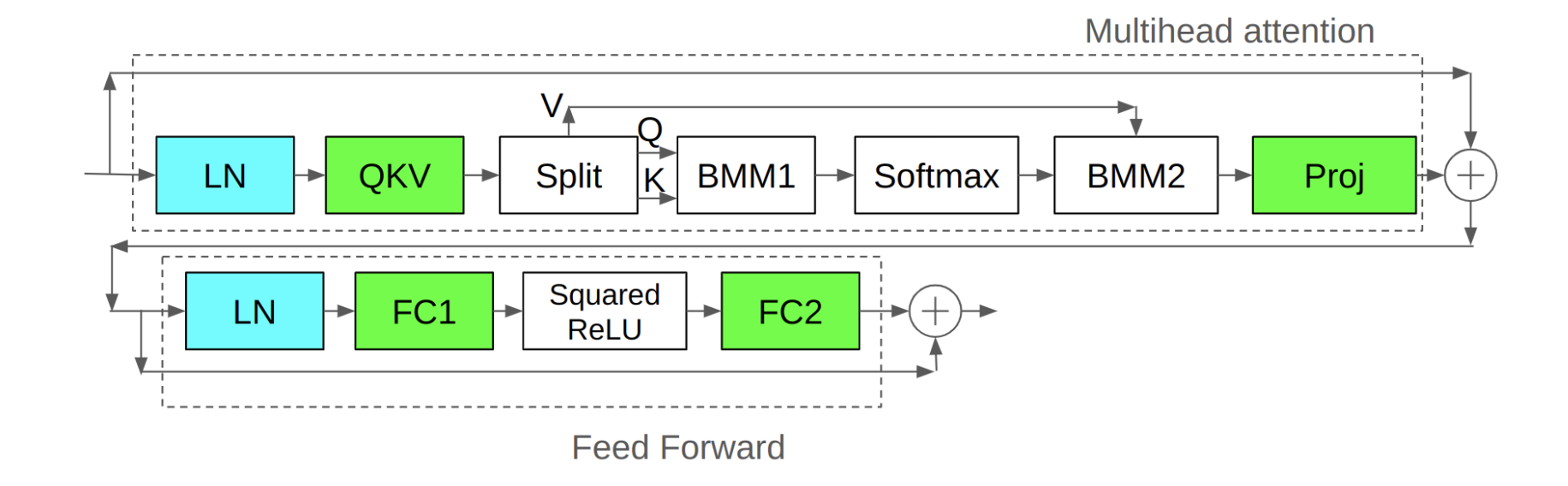
加上 QK 层归一化:
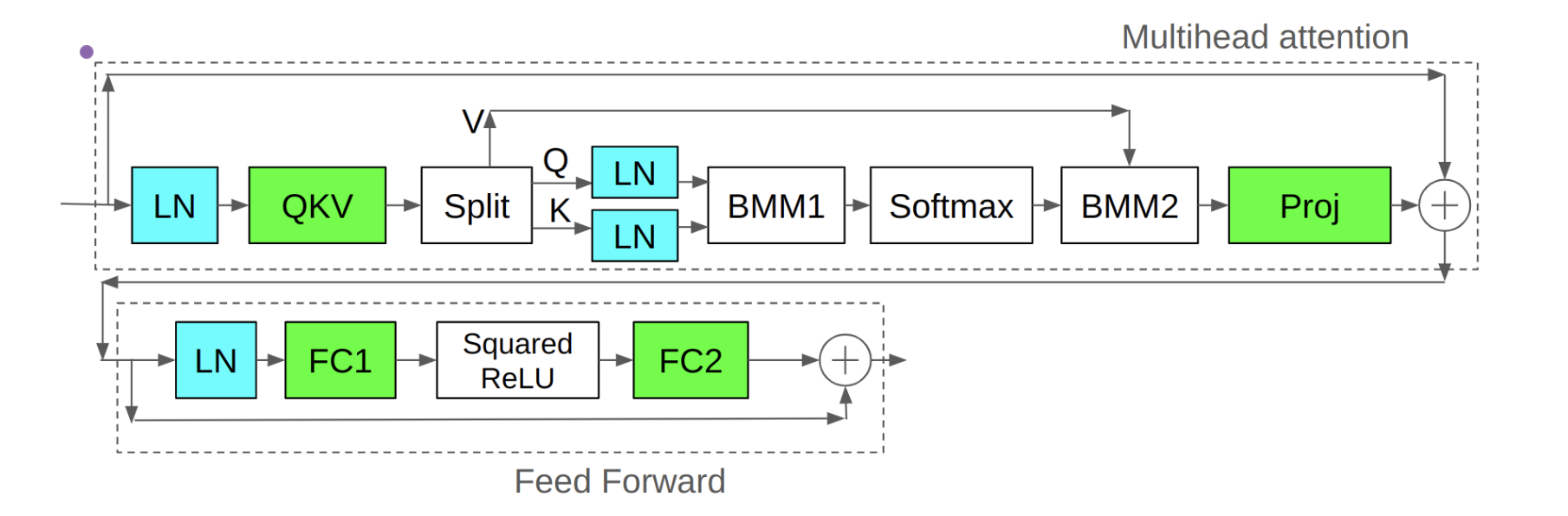
Logit Soft-Capping
通过 Tanh 函数对 logits 进行软截断到某个最大值,以防止 logits 过大:
\[\text{soft_capped_logit} = \text{soft_cap} \times \text{tanh}(\text{logit} / \text{soft_cap})\]该技术可以防止 logits 爆炸,但也可能有性能问题
Attention Heads
注意力机制涉及的计算:
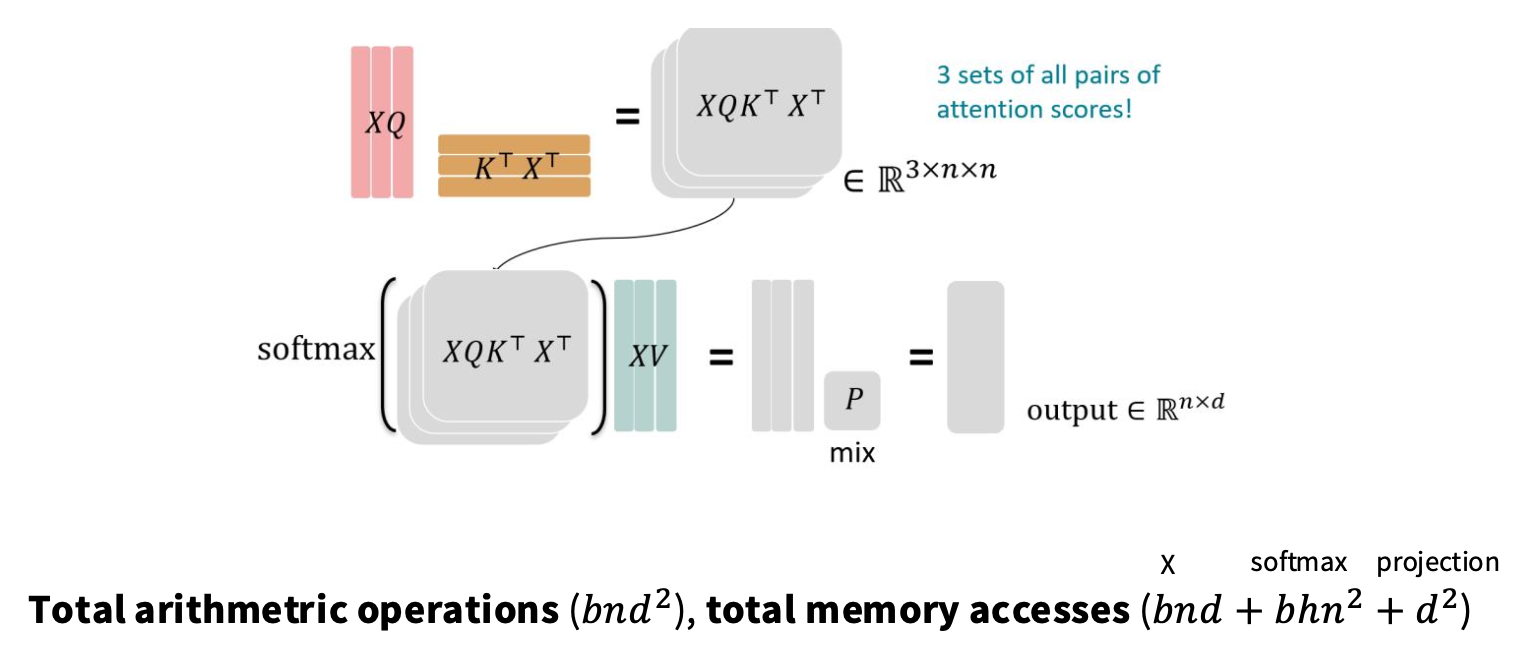
| 操作 | 输入张量 | 输出张量 | FLOPS | 内存访问量(使用 KV cache) |
|---|---|---|---|---|
| Q = X @ W_Q | X (B, N, D)W_Q (D, D) |
Q (B, N, D) |
2 × B × N × D² | B × N × D + B × N × D + D^2(读 X + 写 Q + 读 W_Q) |
| K = X @ W_K | X (B, N, D)W_K (D, D) |
K (B, N, D) |
2 × B × N × D² | B × N × D + B × N × D + D^2(读 X + 写 K + 读 W_K) |
| V = X @ W_V | X (B, N, D)W_V (D, D) |
V (B, N, D) |
2 × B × N × D² | B × N × D + B × N × D + D^2(读 X + 写 V + 读 W_V) |
| Attn = softmax(Q @ K^T) | Q (B, N, D)K (B, N, D) |
Attn (B, N, N) |
2 × B × N² × D + 3 × B × N² | B × N × D + B × N × D + B × H × N × N + B × N × N(读 Q + 读 K + softmax(Q @ K^T) + 写 Attn) |
| Output = Attn @ V | Attn (B, N, N)V (B, N, D) |
Output (B, N, D) |
2 × B × N² × D | B × N × N + B × N × D + B × N × D(读 Attn + 读 V + 写 Output) |
因此算术运算次数为 $O(B × N × D^2 + B × N^2 × D)$。内存访问量为 $O(BND + BHN^2 + D^2)$
推理时无法并行化,生成过程需要逐步进行。在这种情况下需要通过 KV Cache 增量地重新计算/更新注意力。增量算术强度(Arithmetic Intensity)如下:
| 操作 | 输入张量 | 输出张量 | FLOPS | 内存访问量(字节) |
|---|---|---|---|---|
1. QKV 投影q_new = x_new @ W_Qk_new = x_new @ W_Kv_new = x_new @ W_V |
x_new (B, 1, D)W_Q (D, D)W_K (D, D)W_V (D, D) |
q_new (B, 1, D)k_new (B, 1, D)v_new (B, 1, D) |
$2 \times B \times 1 \times D^2 \times 3$ $= 6BD^2$ |
读: - x_new: $B \cdot 1 \cdot D$- W_Q, W_K, W_V: $3 \cdot D^2$写: - q_new, k_new, v_new: $3 \cdot B \cdot 1 \cdot D$总计: $\approx O(BD + D^2)$ |
| 2. 更新 KV Cache ( k_new, v_new → Cache) |
k_new (B, 1, D)v_new (B, 1, D)K_prev (B, t-1, D)V_prev (B, t-1, D) |
K_cache (B, t, D)V_cache (B, t, D) |
0 (内存操作) | 读/写: - 追加操作,访问量约为 $2 \cdot B \cdot 1 \cdot D$ 总计: $O(BD)$ |
| 3. 注意力计算 3.1 Scores = Q @ K^T |
q_new (B, 1, D)K_cache (B, t, D) |
Scores (B, 1, t) |
$2 \times B \times 1 \times t \times D$ $= 2BDt$ |
读: - q_new: $B \cdot 1 \cdot D$- K_cache: $B \cdot t \cdot D$写: - Scores: $B \cdot 1 \cdot t$总计: $O(BDt)$ |
3.2 Softmax(Scores) |
Scores (B, 1, t) |
Attn_Weights (B, 1, t) |
$\sim 3 \times B \times 1 \times t$ $= 3Bt$ (exp, sum, div) |
读: - Scores: $B \cdot 1 \cdot t$写: - Attn_Weights: $B \cdot 1 \cdot t$总计: $O(Bt)$ |
3.3 Output = Attn_Weights @ V |
Attn_Weights (B, 1, t)V_cache (B, t, D) |
Output (B, 1, D) |
$2 \times B \times 1 \times t \times D$ $= 2BDt$ |
读: - Attn_Weights: $B \cdot 1 \cdot t$- V_cache: $B \cdot t \cdot D$写: - Output: $B \cdot 1 \cdot D$总计: $O(BDt)$ |
第 t 步总计 |
FLOPS: $6BD^2 + 4BDt + 3Bt$ $\approx O(BD^2 + BDt)$ |
内存访问: $\approx O(BD + D^2 + BDt)$ |
总算术运算次数 $\approx BND^2$,总内存访问次数 $\approx BN^2D + ND^2$,算术强度 $\approx O\left(\frac{N}{D} + \frac{1}{B}\right)^{-1}$,需要更大批次 + 更短序列长度,或更大的模型维度来提高算法强度。
MQA
核心思想——有多个查询,但共享键和值:
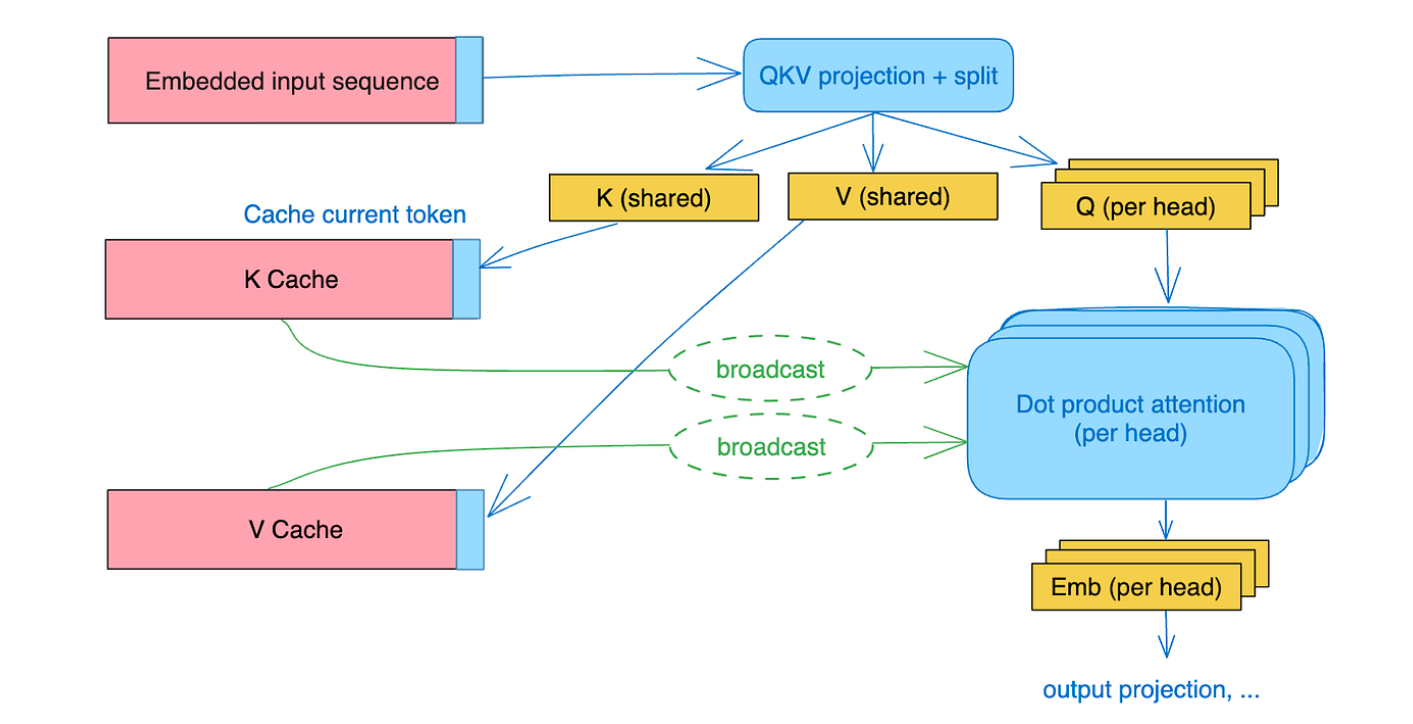
因此需要在内存中移动的 KV Cache 要少得多。
GQA
减少键和值的数量(但不是激进的减少到一个):
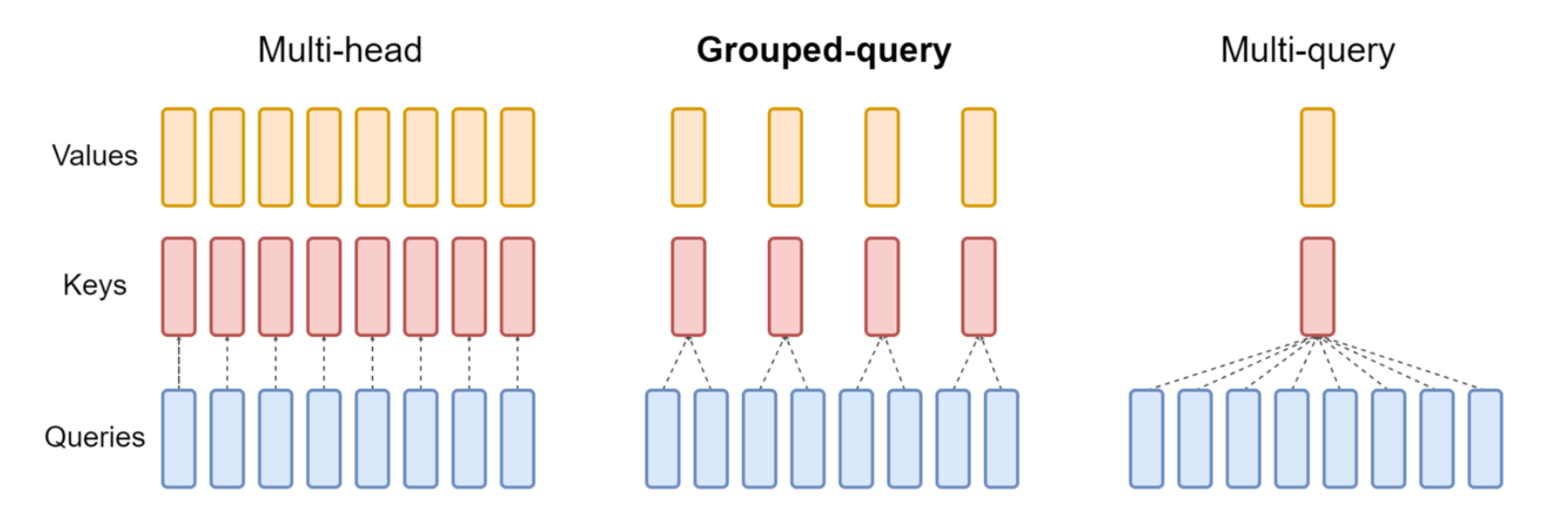
Sparse or sliding window attention
关注整个上下文的计算成本很高(呈平方级增长),可以通过构建稀疏/结构化注意力机制,在表达能力和运行效率之间进行权衡:
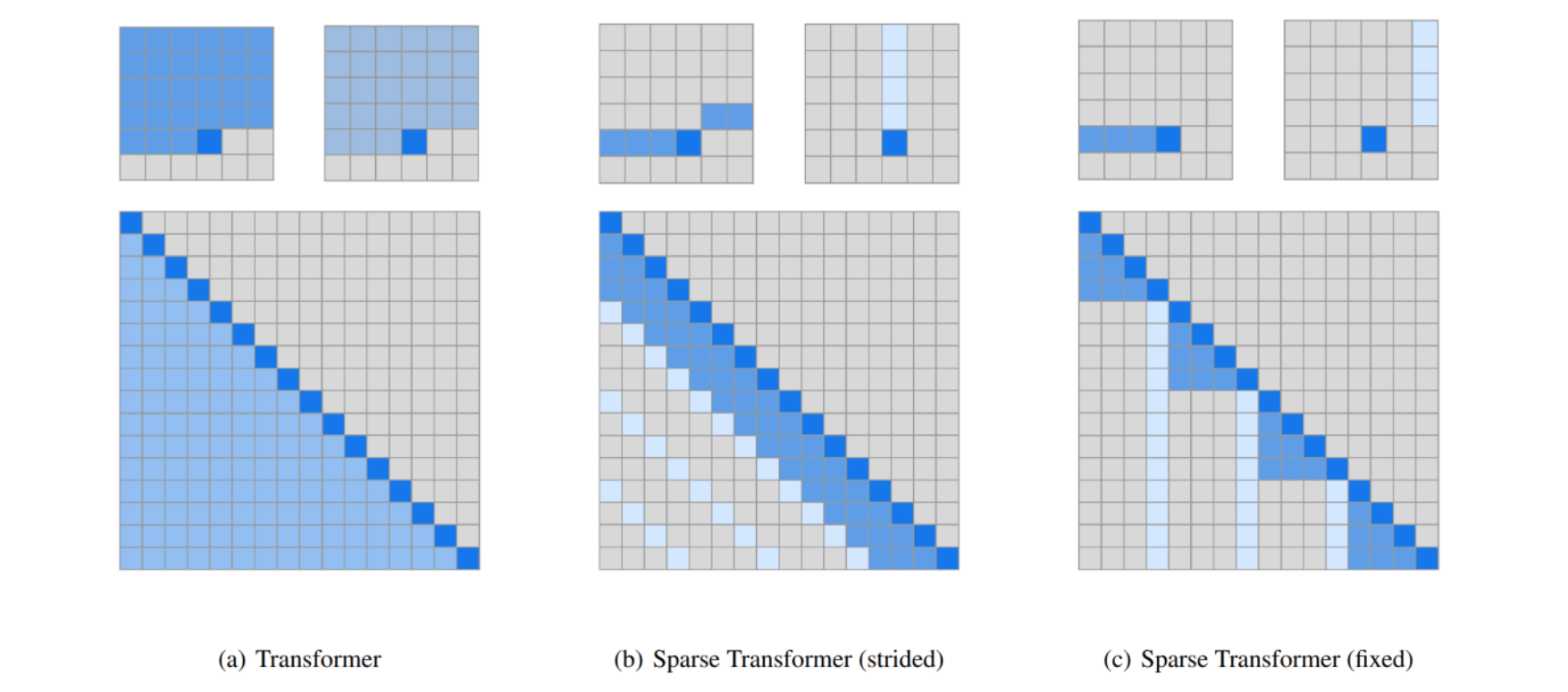
也可以通过滑动窗口注意力机制: