线性回归与单层神经网络

我们可以用神经网络来描述线性回归模型：

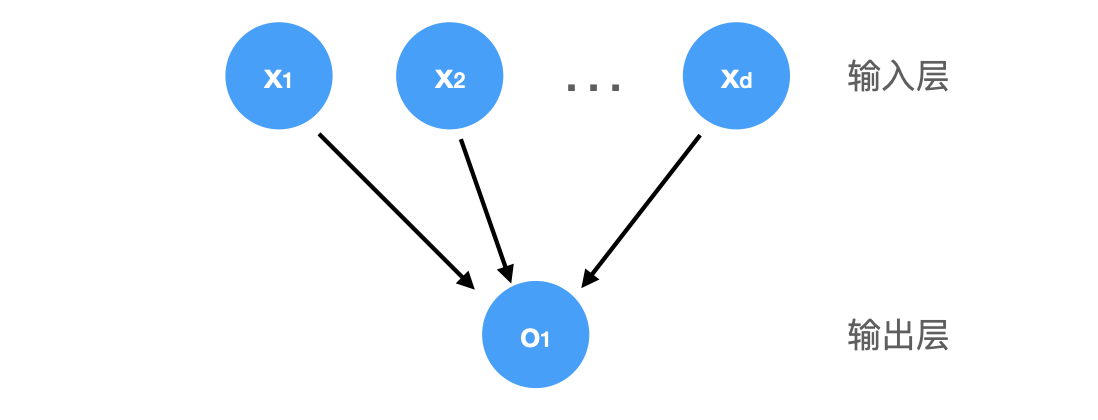
上图所示的神经网络中，输入为 $ x_1, \ldots, x_d $，因此输入层中的输入数（或称为特征维度 feature dimensionality）为 $d$。 网络的输出为 $o_1$，因此输出层中的输出数是 $1$。通常计算神经网络的层数时不考虑输入层，因此上图的神经网络层数为 $1$。线性回归模型可以视为一个单层神经网络：

对于线性回归，输出和输入的全部特征维度都相关联，通常将这种变换称为全连接层（fully-connected layer）或者稠密层（dense layer）。

使用 pytorch 或 tensorflow 可以很方便的创建一个全连接层，代码如下：

PyTorch 版本

1
2
3
4
# nn是神经网络的缩写
from torch import nn
# 2 为输入层的维度，1 为输出层的维度
net = nn.Sequential(nn.Linear(2, 1))

TensorFlow 版本

1
2
3
net = tf.keras.Sequential()
# Keras 无需指定输入层的维度
net.add(tf.keras.layers.Dense(1))

Softmax 回归

前面提到，线性回归一般解决的是单个或多个连续值的预测问题。如果想解决分类问题的预测，首先需要明确如何表示分类（即标签 label）。统计学中通常采用独热编码（one-hot encoding）来表示分类。 独热编码是一个向量，维数和类别一样多。 类别对应的分量设置为 $ 1 $，其他所有分量设置为 $ 0 $。

如果想用全连接层来解决分类问题，则需要输出单一值变成输出多个值：

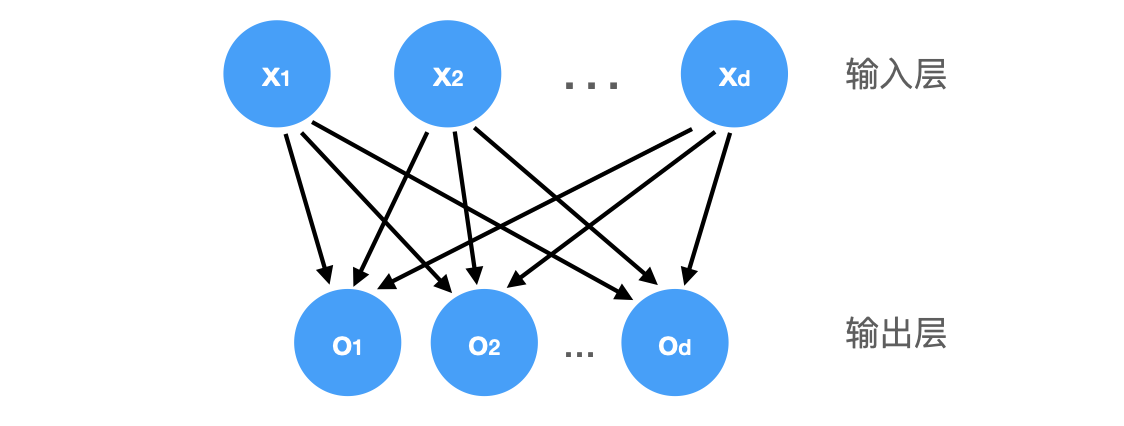
输出值的个数对应类别的个数。上图同样为单层神经网络，可以用 $\mathbf{o} = \mathbf{W} \mathbf{x} + \mathbf{b}$ 来表示。

我们需要将输出转换为类别的概率向量，则需要满足：每个输出的取值区间位于 $[0, 1]$，所有输出加起来和为 $1$。通常会采用 softmax 函数来对输出 $\mathbf{o}$ 进行转换：

求幂保证了输出非负，除以总和保证了输出之和为 $1$。同时 softmax 不会改变输出的大小顺序，因此预测时可以采用下式：

尽管 softmax 是一个非线性函数，但 softmax 回归的输出仍然由输入特征的仿射变换决定。 因此softmax 回归属于线性模型（linear model）。

Log Softmax

softmax 函数会有数值不稳定的风险，有可能造成数值上溢（overflow）或下溢（underflow）。

数值上溢

前面提到 softmax 公式 $\hat y_j = \frac{\exp(o_j)}{\sum_k \exp(o_k)}$，当 $o_k$ 数值很大时，$\exp(o_k)$ 可能会大于数据类型的上限，引发上溢。在 python 中这可能会导致分子或分母变成 inf，最后计算出 0、inf 或 nan 的 $\hat y_j$。

其中一个解决方法是，计算 softmax 前，先从所有 $o_k$ 中减去 $\max(o_k)$：

数值下溢

减去 $\max(o_k)$ 可以解决上溢问题，但有可能引起下溢。如果 $o_j - \max(o_k)$ 是一个比较大的负值，$\exp(o_j - \max(o_k))$ 将会接近于 $0$，四舍五入后可能会导致 $\hat y_j$ 为 $0$，$\log(\hat y_j)$ 为 -inf（交叉熵损失函数需要计算 $\log(\hat y_j)$，具体见 线性回归、损失函数以及梯度下降 ），导致反向传播出现 nan。

log softmax

上面提到，计算交叉熵损失函数时，我们实际计算的是 $ \log(\hat y_j) $：

通过将 softmax 和 log 组合在一起，我们无需计算 $\exp(o_j - \max(o_k))$ 而是直接计算 $o_j - \max(o_k)$ ，规避了数值溢出的问题，这个属于 LogSumExp Trick，可以参考最底下的文章。

多层感知机（MLP）

隐藏层

线性意味着单调，可以通过在网络中加入一个或多个隐藏层来克服线性模型的限制， 使其能处理更普遍的函数关系类型。 要做到这一点，最简单的方法是将许多全连接层堆叠在一起。 每一层都输出到上面的层，直到生成最后的输出。

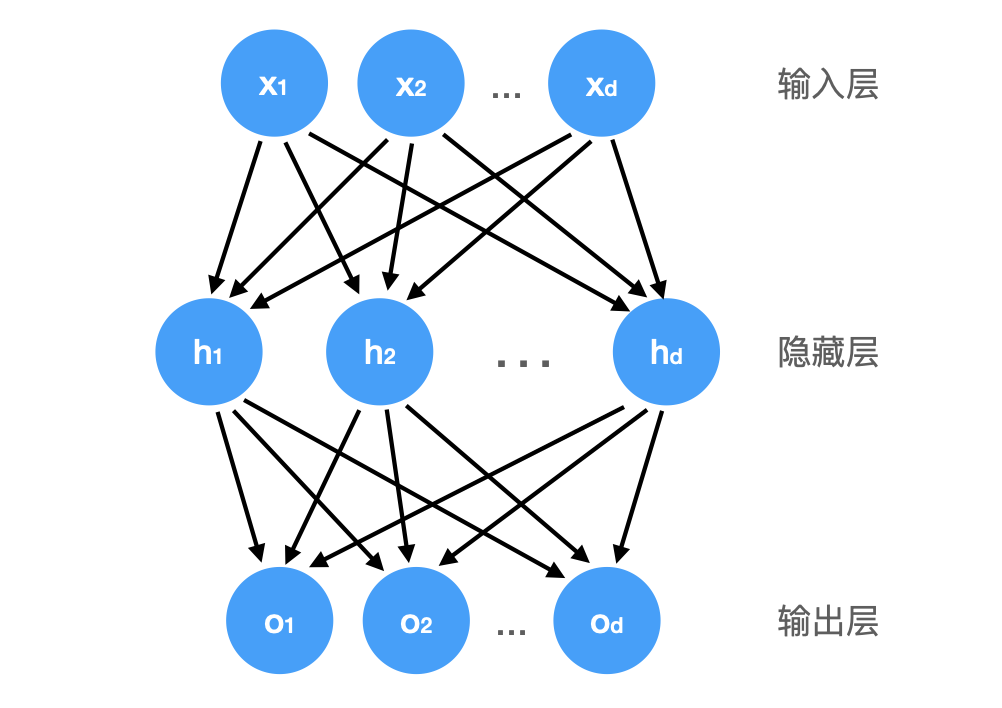
这种架构通常称为多层感知机（multilayer perceptron），通常缩写为 MLP。注意，MLP 中每一层都是全连接的。 每个输入都会影响隐藏层中的每个神经元， 而隐藏层中的每个神经元又会影响输出层中的每个神经元。

线性到非线性

用 $\mathbf{H} \in \mathbb{R}^{n \times h}$ 表示隐藏层的输出，$\mathbf{O} \in \mathbb{R}^{n \times q}$ 表示多层感知机的输出，可得：

可得：

其中：

可见添加隐藏层，得到的依然是线性模型，并没有带来额外的好处。我们还需要关键要素： 在仿射变换之后对每个隐藏单元应用非线性的激活函数（activation function）$\sigma$。从而使线性模型进化成非线性模型：

激活函数

Sigmoid

定义

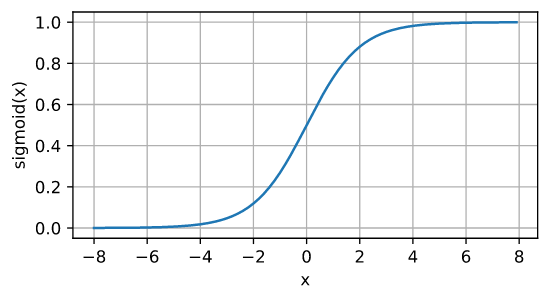
导数

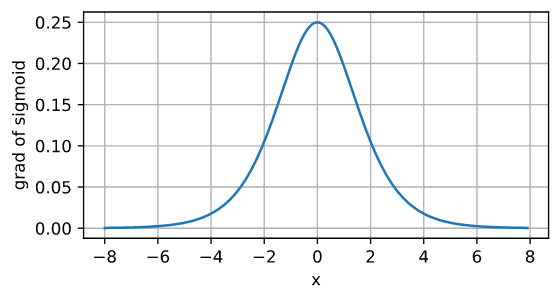
优点

• 对每个神经元的输出进行了归一化，输出范围是 0 到 1
• 函数可微

缺点

• 从图像可以看出，输入太大或太小都会使其梯度接近 0，在反向传播中梯度接近 0，参数就会难以更新，容易造成梯度消失。另外从图中可以看出，sigmoid 的导数取值阈值为 $[0, 0.25]$，即使取最大值 0.25，经过多层神经网络反向传播，0.25 连乘之后也会变得特别小，出现梯度消失。具体分析见下文“BP 算法”。

• sigmoid 输出不是 0 均值的，会影响模型收敛速度。分析如下：

  梯度下降是通过求偏导来更新参数的：

  \[w \gets w - \eta\cdot\frac{\partial L}{\partial w}\]

  对于某个神经元来说，输入输出公式为，$\sigma$ 为激活函数：

  \[\sigma(\vec x; \vec w, b) = \sigma(z) = \sigma\Bigl(\sum_iw_ix_i + b\Bigr)\]

  可得：

  \[\frac{\partial L}{\partial w_i} = \frac{\partial L}{\partial \sigma}\frac{\partial \sigma}{\partial z}\frac{\partial z}{\partial w_i} = x_i \cdot \frac{\partial L}{\partial \sigma}\frac{\partial \sigma}{\partial z}\]

  参数更新公式如下：

  \[w_i \gets w_i - \eta x_i\cdot \frac{\partial L}{\partial \sigma}\frac{\partial \sigma}{\partial z}\]

  $\frac{\partial L}{\partial \sigma}\frac{\partial \sigma}{\partial z}$ 对于 $w_i$ 来说是常数，因此 $w_i$ 更新方向是由输入值 $x_i$ 决定。如果 $x_i$ 和 $x_j$ 符号相同，则 $w_i$ 和 $w_j$ 更新方向就相同，反之则相反。

  在 sigmoid 函数中，输出值始终为正，这意味着如果上一层采用了 sigmoid 作为激活函数，那参数 $w_i, w_j, …$ 只能往相同的方向更新，导致模型收敛的时间变慢。

• 指数运算较慢

ReLU

定义

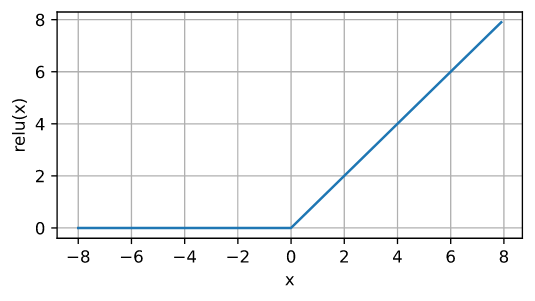
导数

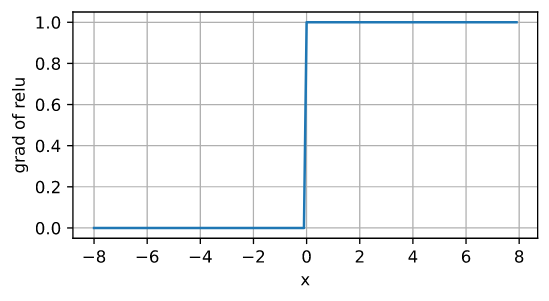
优点

• 在输入大于 0 的时候导数为 1，反向传播中导数连乘也不会出现梯度消失。
• 计算速度快

缺点

• 输出不是 0 的均值，和 sigmoid 一样的问题

• Dead ReLU 问题，部分神经元永远不会被激活。ReLU 在输入为负数时，梯度为 0，这就导致反向传播时各层的梯度都为 0，无法再更新参数。

  产生这种现象的两个原因：

  • 参数初始化问题
  • learning rate 太高导致在训练过程中参数更新太大

  解决方案：

  • 采用 Xavier 初始化方法
  • 避免将 learning rate 设置太大或使用 adagrad 等自动调节 learning rate 的算法
  • Leaky ReLU/PReLU/ELU

Tanh

定义

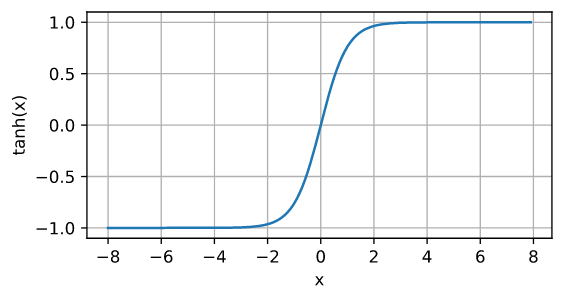
导数

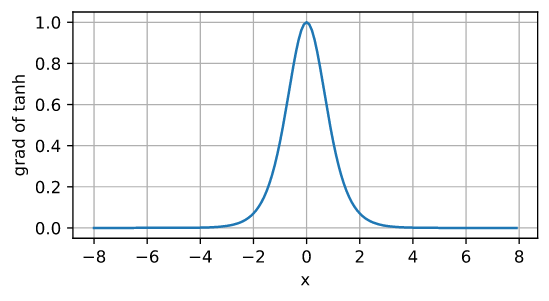
优缺点和 sigmoid 类似。

反向传播 BackPropagation

BackPropagation （BP），即“误差反向传播”的简称，是一种与最优化方法（如梯度下降法）结合使用的，用来训练神经网络的常见方法。上一篇文章我们介绍了梯度下降和误差函数，这里介绍下在 BP 算法中如何结合以优化神经网络参数。

符号定义

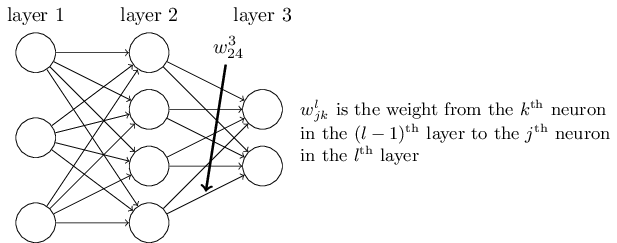
定义 $w^l_{jk}$ 表示第 $(l-1)^{\rm th}$ 层第 $k^{\rm th}$ 个神经元和第 $l^{\rm th}$ 层第 $j^{\rm th}$ 个神经元之间的 weight，注意这里 $k$ 是输入层，$j$ 是输出层：

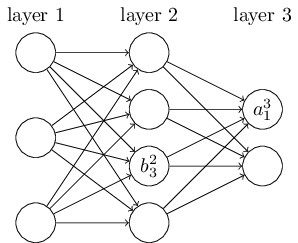
定义 $b^l_j$ 作为第 $l^{\rm th}$ 层第 $j^{\rm th}$ 个神经元的 bias，定义 $a^l_j$ 作为第 $l^{\rm th}$ 层第 $j^{\rm th}$ 个神经元的 activation（激活函数的输出）：

可得：

定义第 $l^{\rm th}$ 层的 weight matrix 为 $w^l$，其中第 $j^{\rm th}$ 行第 $k^{\rm th}$ 列的元素 $w^l_{jk}$ 表示第 $(l-1)^{\rm th}$ 层第 $k^{\rm th}$ 个神经元和第 $l^{\rm th}$ 层第 $j^{\rm th}$ 个神经元之间的 weight。类似的，定义第 $l^{\rm th}$ 层的 bias vector 为 $b^l$，activation vector 为 $a^l$。可以将上式重写为：

上一层的输出作为这一层的输入，乘以 weight matrix，加上 bias vector 得到 activations，然后再作为下一层的输入，以此推进直到最后一层。

为方便下面的推导，定义 $z^l \equiv w^l a^{l-1}+b^l$，$z^l$ 指第 $l^{\rm th}$ 层的 weighted input，也即第 $l^{\rm th}$ 层的激活函数的输入，可得 $a^l = \sigma(z^l)$。

误差函数

这里使用 MSE 作为误差函数：

单个样本的误差为：

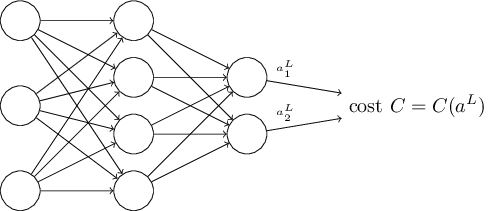
可以看出，误差函数是关于 activations $a^L$ 的函数。注意这里输入 $x$ 和对应的 $y$ 都是固定的，因此误差函数不是关于 $y$ 的函数。

四个公式

假设在第 $l^{\rm th}$ 层第 $j^{\rm th}$ 个神经元的 weighted input 加上一个极小的偏移值 $\Delta z^l_j$，则该神经元的输出为 $\sigma(z^l_j+\Delta z^l_j)$。这个偏差会一直传递到最后一层，带给误差 $\frac{\partial C}{\partial z^l_j} \Delta z^l_j$ 的偏移。

而我们的目标是减小误差，如果 $\frac{\partial C}{\partial z^l_j}$ 非常大（正数或者负数），则 $\Delta z^l_j$ 取和 $\frac{\partial C}{\partial z^l_j}$ 相反的符号即可以大大减小误差。如果 $\frac{\partial C}{\partial z^l_j}$ 非常小接近零，则 $\Delta z^l_j$ 取正负对误差都影响不大。因此可以认为 $\frac{\partial C}{\partial z^l_j}$ 是对神经元误差的评估。定义 $\delta^l_j$ 为第 $l^{\rm th}$ 层第 $j^{\rm th}$ 个神经元的误差，$\delta^l_j \equiv \frac{\partial C}{\partial z^l_j}$。定义 $\delta^l$ 为第 $l^{\rm th}$ 层的误差向量。BP 算法会计算每一层的 $\delta^l$，并关联到 $\partial C / \partial w^l_{jk}$ 和 $\partial C / \partial b^l_j$，即通过 BP 算法计算出神经网络参数 $w$ 和 $b$ 的梯度，得以更新 $w$ 和 $b$ 以减少误差。

公式 1

输出层的误差 error in the output layer $\delta^L_j$ 定义如下：

如果是 MSE 误差函数 $C = \frac{1}{2} \sum_j (y_j-a^L_j)^2$，可得 $\partial C / \partial a^L_j = (a_j^L-y_j)$。

定义 $\nabla_a C$ 为 $\partial C / \partial a^L_j$ 构成的向量，矩阵形式的公式如下：

代入 $\nabla_a C = (a^L-y)$ 可得：

$BP1$ 证明

根据链式法则：

$a^L_k$ 只取决于 $z^L_k$，因此当 $k≠j$ 时 $∂a^L_k/∂z^L_j$ 为 $0$，因此可得 $δ^L_j=\frac{∂C}{∂a^L_j}\frac{∂a^L_j}{∂z^L_j}=\frac{∂C}{∂a^L_j}σ′(z^L_j)$ 。

公式 2

由 $\delta^{l+1}$ 推导 $\delta^l$ 的公式如下：

这里体现了 backward 的过程，将误差从后一层往前一层回溯。通过 $BP1$ 计算最后一层输出层的误差，再通过 $BP2$ 计算前一层的误差，以此类推，就可以计算出每一层的误差。

$BP2$ 证明

根据链式法则：

公式 3

$BP3$ 证明

\(\frac{∂(∑\limits_jw^l_{kj}a^{l−1}_j+b^l_k)}{∂b^l_j}$项中 $∑\limits_jw^l_{kj}a^{l−1}_j$ 与 $b^l_j$ 无关，因此为 $0$。当 $k≠j$ 时，$\frac{∂(b^l_k)}{∂b^l_j}$为 $0$。只有当 $k=j$ 时，$\frac{∂(b^l_k)}{∂b^l_j}$ 才为 $1\)。

公式 4

上式可以重写为：

$BP4$ 证明

右边部分只有在 $a=j,b=k$ 时才不为0，此时就可以去掉求和符号得到：

BP 算法

1. Input $x$: 计算出输入层对应的 activation $a^1$
2. Feedforward: 对第 $l=2,3,…,L$ 层，依次计算每一层的 $z^l=w^la^{l−1}+b^l$ 和 $a^l=σ(z^l)$
3. Output error $δ^L$: 得到输出层的结果后，计算输出层的误差 $δ^L=∇_aC⊙σ′(z^L)$
4. Backpropagate the error: 对第 $l=L−1,L−2,…,2$ 层，从后往前依次计算每一层的误差 $δ^l=((w^{l+1})^Tδ^{l+1})⊙σ′(z^l)$
5. Output: 得到每一层的误差后，就可以计算出每一层参数 $w$ 和 $b$ 的梯度 $\frac{∂C}{∂w^l_jk}=a^{l−1}_kδ^l_j$ 和$\frac{∂C}{∂b^l_j}=δ^l_j$

梯度消失

当采用 sigmoid 做激活函数时，输出接近 $0$ 或 $1$ 时，曲线变得很平， $\sigma’(z^L_j) \approx 0$：

从 $BP1$ 公式可知，$\sigma’(z^L_j) \approx 0$ 会导致 $δ^L_j \approx 0$，从 $BP3$ 和 $BP4$ 可知 $δ^L_j \approx 0$ 会导致输出层的参数 $w$ 和 $b$ 的梯度接近于 $0$，参数更新缓慢。

从 $BP2$ 公式可知，不止最后一层，每一层如果 $\sigma’(z^l_j) \approx 0$，且 $w^{l+1}_{kj}$ 不够大时，都会造成梯度消失，导致参数更新缓慢。且从 $BP2$ 还可以看出，误差会从输出层逐层往回连乘的，sigmoid 导数的最大值为 0.25，在深度神经网络中连乘 N 次之后会变得非常小，这就是为什么 sigmoid 激活函数容易造成梯度消失。在深度神经网络中 relu 是更常用的激活函数。

参考文献

• 动手学深度学习
• 关于LogSumExp
• The Log-Sum-Exp Trick
• 常见激活函数优缺点与dead relu problem
• Neural Networks and Deep Learning
• Why are deep neural networks hard to train?

• Previous
  线性回归、损失函数以及梯度下降
• Next
  极大似然和损失函数