从全连接层到卷积
全连接层中,每个神经元彼此相连:
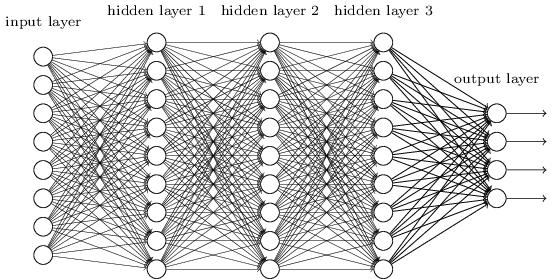
在做图像识别时,以 $28 \times 28$ 的图像为例,会将其展平为 $784$($= 28 \times 28$)个元素的向量作为神经网络的输入,但展平后会丢失了像素的空间信息。
而卷积神经网络是局部连接的,并且输入保留了空间信息,因此经常被用于图像识别。卷积神经网络的常见架构如下:
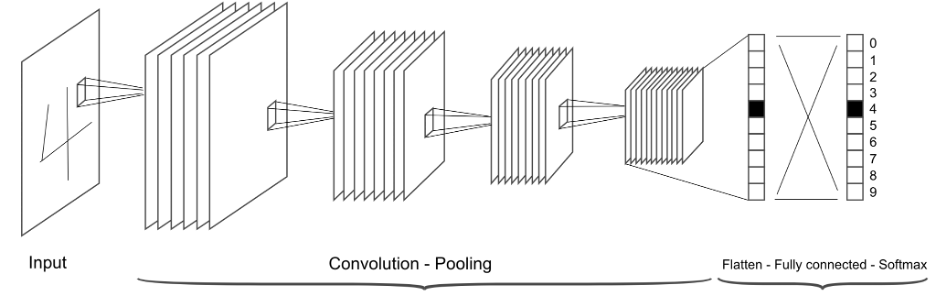
卷积神经网络的核心就是卷积层。在数学中“卷积”被定义为:
\[(f * g)(\mathbf{x}) = \int f(\mathbf{z}) g(\mathbf{x}-\mathbf{z}) d\mathbf{z}\]卷积是测量 $f$ 和 $g$ 之间的重叠。如果是离散对象,则积分变成求和:
\[(f * g)(i) = \sum_a f(a) g(i-a)\]对于二维张量,则为 $f$ 的索引 $(a,b)$ 和 $g$ 的索引 $(i-a, j-b)$ 上的对应和:
\[(f * g)(i, j) = \sum_a\sum_b f(a, b) g(i-a, j-b)\]但在卷积神经网络里,卷积更准确来说不是数学上定义的卷积运算,而是互相关运算(cross-correlation)。定义二维图像 $\mathbf{X}$ 为输入,每次只检查距离当前位置 $(a,b)$ 不超过$\Delta$ 的区域,则互相关运算输出 $\mathbf{H}$ 如下:
\[[\mathbf{H}]_{i, j} = u + \sum_{a = -\Delta}^{\Delta} \sum_{b = -\Delta}^{\Delta} [\mathbf{V}]_{a, b} [\mathbf{X}]_{i+a, j+b}\]上式中的 $\mathbf{V}$ 被称为卷积核(kernel),又称为滤波器(filter)。卷积核是卷积层中可学习的权重矩阵。下面以 $3 \times 3$ 的输入,$2 \times 2$ 的卷积核为例,执行互相关运算如下:
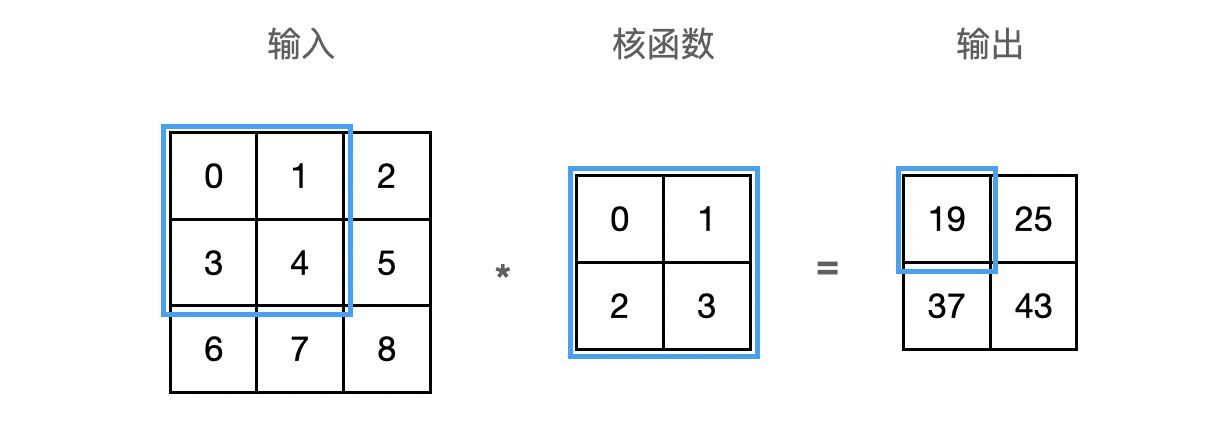
卷积核 $\mathbf{V}$ 从输入的左上角开始,从左到右、从上到下滑动。 当卷积核滑动到新一个位置时,对应位置的输入与卷积核进行按元素相乘,得到 $\mathbf{H}$ 再求和得到单个输出标量值。上图中运算如下:
\[0\times0+1\times1+3\times2+4\times3=19\]最终得到的输出有时称为特征映射(feature map)。
整体流程如下:
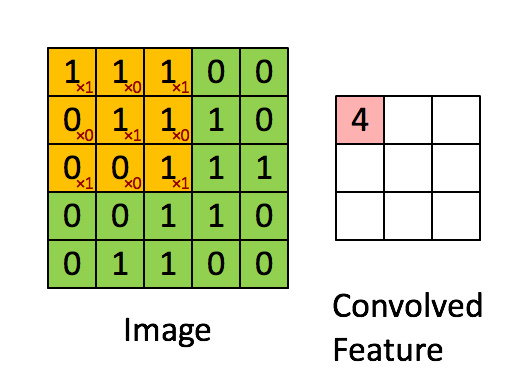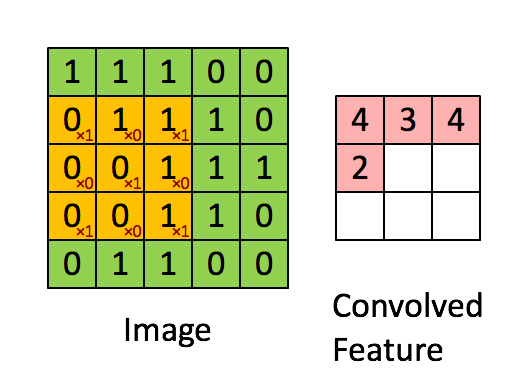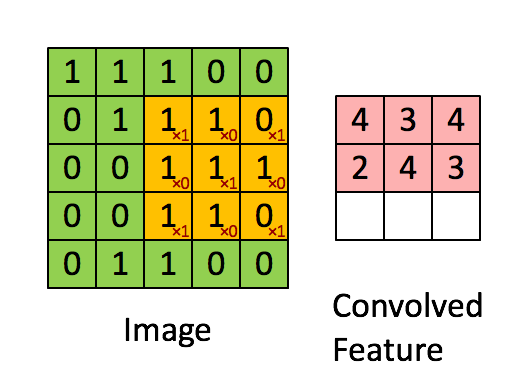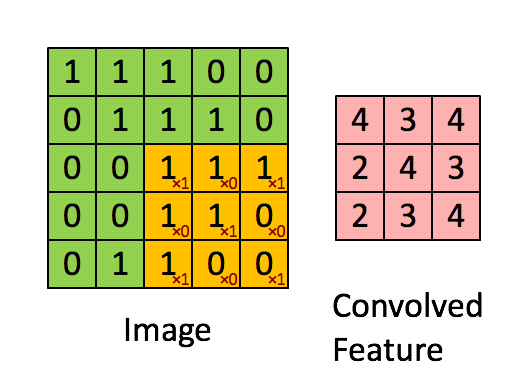
局部感知野 Local Receptive Field
感受野(Receptive Field)指的是神经网络中神经元“看到的”输入区域。卷积神经网络是局部连接的,特征映射中某个元素的计算只受输入图像上某部分区域的影响,这个区域即该元素的局部感受野。
在卷积神经网络中,越靠后的卷积层看到的输入区域越大,如下图:
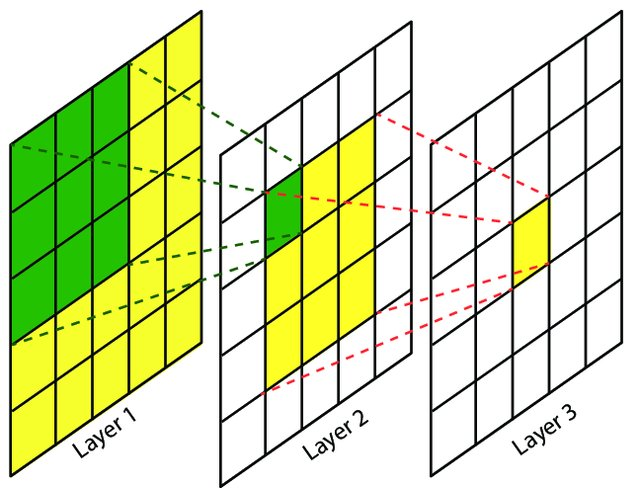
因此,卷积神经网络前面几层主要提取局部特征,后面几层主要提取整体特征。
权值共享
权值即卷积核(滤波器)中的权重矩阵。权值共享指多个卷积核共用一个权重矩阵。权值共享在卷积神经网络中起到显著减少网络参数数量的作用。为什么权值可以共享?因为模式和其在图像中出现的位置是无关的。如果相同的模式出现在输入图像中 $(x_1,y_1)$ 以及 $(x_2, y_2)$ 区域,如果卷积核(滤波器)可以在位置 $(x_1,y_1)$ 提取出特征,那它应该也可以在位置 $(x_2, y_2)$ 提取出特征。因此每一层隐藏层所有神经元可学习的权值是共享的,即参数 $w$ 和 $b$ 是共享的。

填充和步幅
在应用多层卷积时,我们常常丢失边缘像素。 由于我们通常使用小卷积核,因此对于任何单个卷积,我们可能只会丢失几个像素。 但随着我们应用许多连续卷积层,累积丢失的像素数就多了。 解决这个问题的简单方法即为填充(padding):在输入图像的边界填充元素(通常填充元素是 0)。下图将 $3×3$ 输入填充到 $5×5$,那么它的输出就增加为 $4×4$:
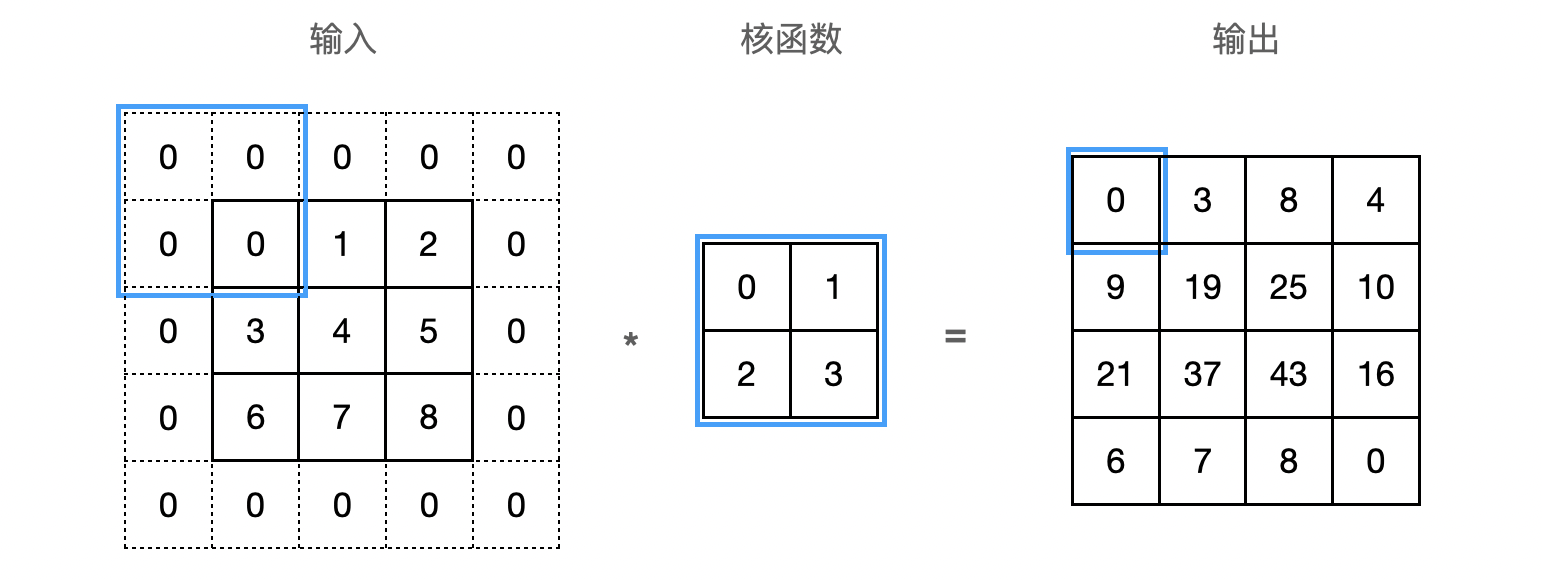
在计算互相关时,卷积窗口从输入张量的左上角开始,向下、向右滑动。 默认每次滑动一个元素。 但是,有时候为了高效计算或是缩减采样次数,卷积窗口可以跳过中间位置,每次滑动多个元素。每次滑动元素的数量称为步幅(stride)。下图是垂直步幅为 $3$,水平步幅为 $2$ 的二维互相关运算:
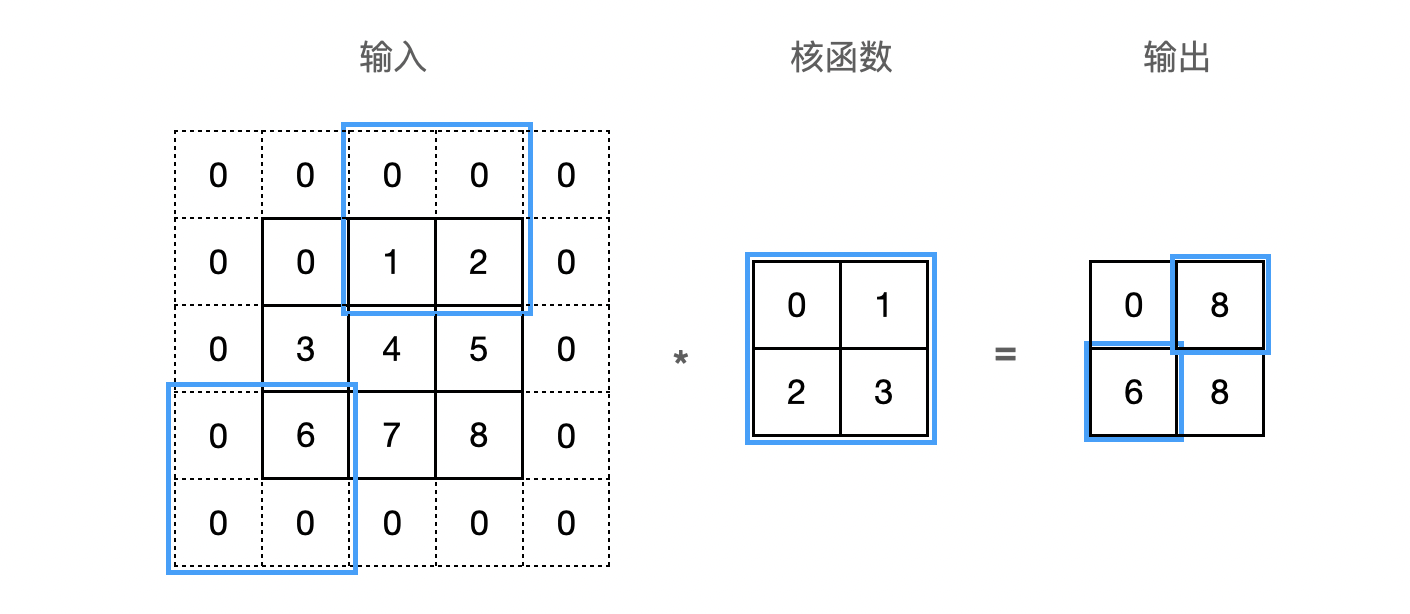
多输入多输出通道
多输入通道
当输入包含多个通道时,比如图像通常包括 RGB 三个通道,需要构造一个与输入数据具有相同输入通道数的卷积核,以便与输入数据进行互相关运算。假设输入的通道数为 $c_i$,那么卷积核的输入通道数也需要为 $c_i$:
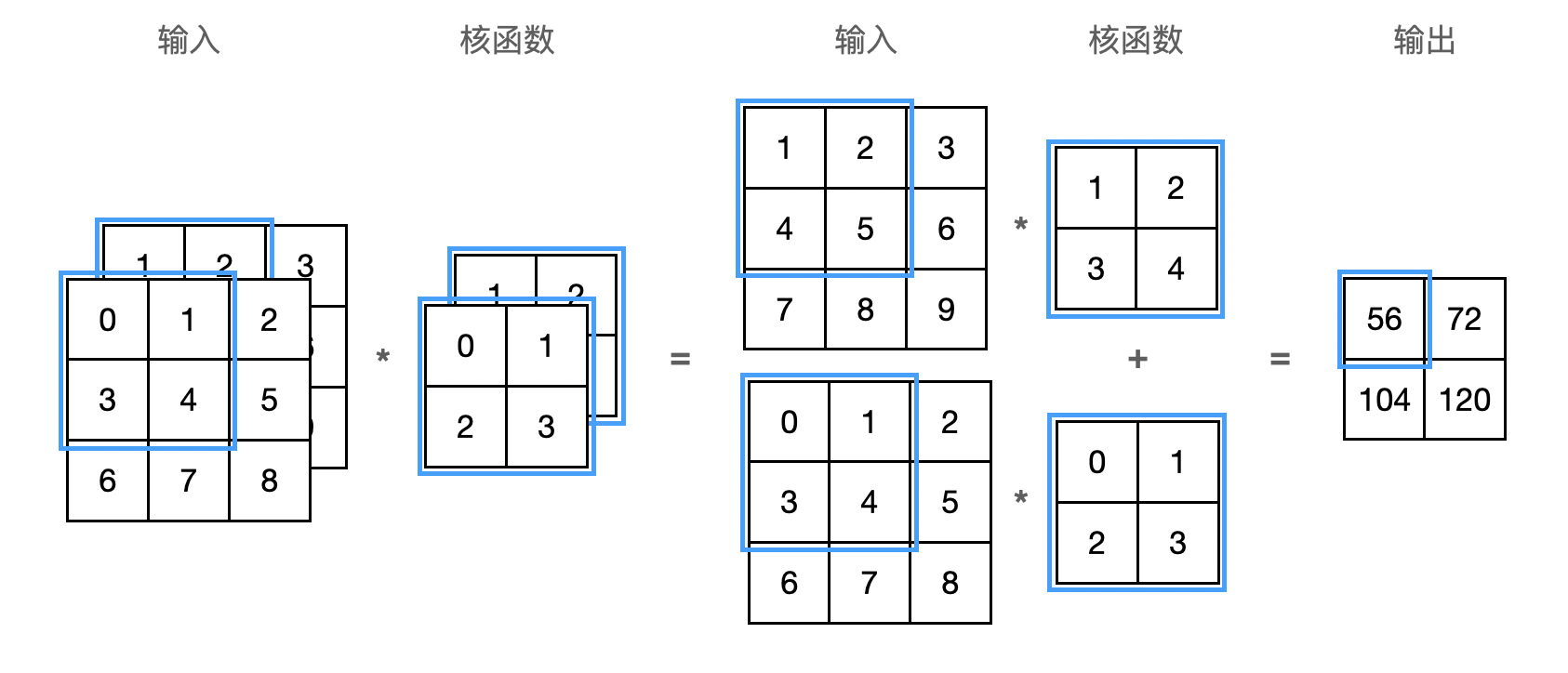
多输出通道
在最流行的神经网络架构中,随着神经网络层数的加深,通常会增加输出通道的维数,通过减少空间分辨率以获得更大的通道深度。直观地说,我们可以将每个通道看作是对不同特征的响应。
用 $c_i$ 和 $c_o$ 分别表示输入和输出通道的数目,并让 $k_h$ 和 $k_w$ 为卷积核的高度和宽度。为了获得多个通道的输出,每个输出通道创建一个形状为 $c_i\times k_h\times k_w$ 的卷积核,这样卷积核的形状是 $c_o\times c_i\times k_h\times k_w$。在互相关运算中,每个输出通道先获取所有输入通道,再以对应该输出通道的卷积核计算出结果。
$1 \times 1$ 卷积层
$1 \times 1$ 卷积,即 $k_h = k_w = 1$,看起来似乎没有多大意义,但十分流行,经常包含在复杂深层网络的设计中。使用 $1 \times 1$ 窗口,就失去了卷积层的特有能力——在高度和宽度维度上,识别相邻元素间相互作用的能力。 其实 $1 \times 1$ 卷积的唯一计算发生在通道上。我们可以将 $1 \times 1$ 卷积层看作是在每个像素位置应用的全连接层,以 $c_i$ 个输入值转换为 $c_o$ 个输出值:
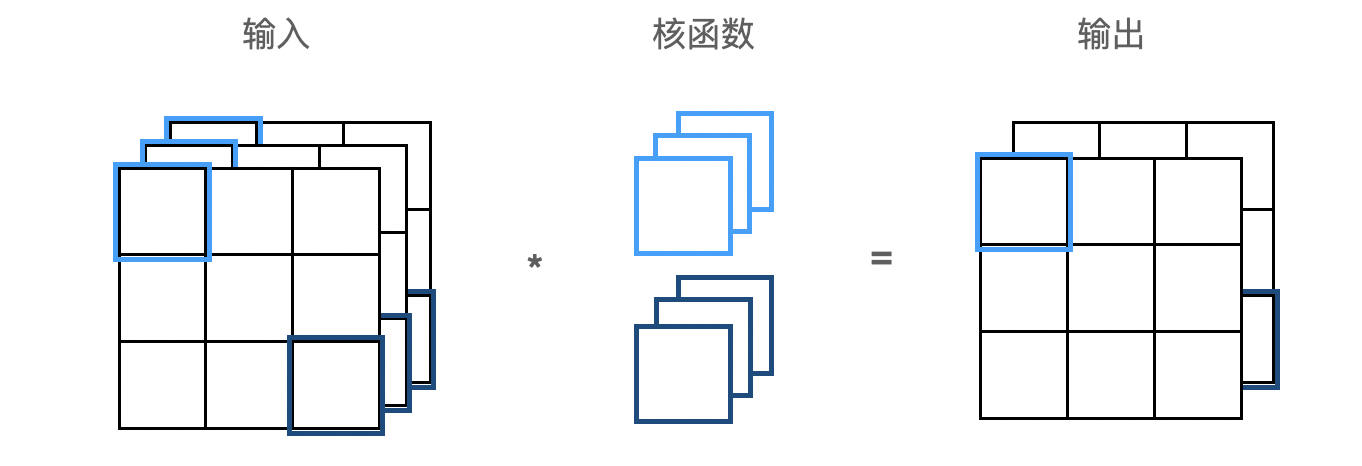
汇聚层
通常当处理图像时,我们希望逐渐降低隐藏表示的空间分辨率、聚集信息,这样随着在神经网络中层叠的上升,每个神经元对其敏感的感受野(输入)就越大。
而机器学习任务通常会跟全局图像有关(例如,“图像是否包含一只猫呢?”),最后一层的神经元应该对整个输入的全局敏感。通过逐渐聚合信息,生成越来越粗糙的映射,最终实现学习全局表示的目标。
在连续卷积层之后加上汇聚层,可以起到聚合数据的作用,能减少网络中参数的数量,使得计算资源耗费变少,有效控制过拟合,并提取重要特征。
与卷积层类似,汇聚层运算符由一个固定形状的窗口组成,该窗口根据其步幅大小在输入的所有区域上滑动,为固定形状窗口(有时称为汇聚窗口)遍历的每个位置计算一个输出。
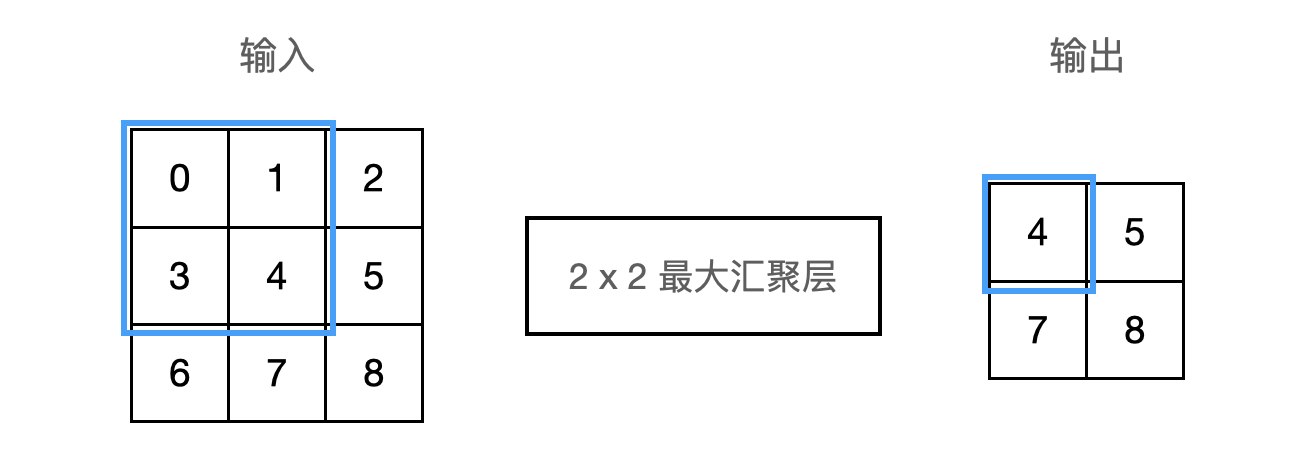
不同于卷积层中的输入与卷积核之间的互相关计算,汇聚层不包含参数。池运算是确定性的,我们通常计算汇聚窗口中所有元素的最大值或平均值。这些操作分别称为最大汇聚层(maximum pooling)和平均汇聚层(average pooling)。下图为 $2 \times 2$ 最大汇聚层的例子:
实践
https://zh.d2l.ai/chapter_computer-vision/neural-style.html 风格迁移