过拟合和欠拟合
过度拟合指着模型对训练集的模拟和学习过度贴合。训练时的检测率很高效果很好,但实际检验时效果很差,即泛化能力不足。用于对抗过拟合的技术称为正则化(regularization)。
欠拟合是指模型和数据集间的拟合程度不够,学习不足。可能是学习轮数不够、数据集特征不规则、模型选择有问题等。欠拟合时,模型的泛化能力同样会很差。

权重衰减 Weight Decay
从模型的复杂度上解释:更小的权值,从某种意义上说,表示网络复杂度更低,对数据的拟合更好。直观来说,权重越大,模型的曲线越“陡峭”,因而能够去拟合到那些位置较偏的点,这就会导致了过拟合。
权重衰减(weight decay)是最广泛使用的正则化的技术之一, 它通常也被称为 $L2$ 正则化。将权重向量的 $L2$ 范数作为惩罚项加到损失函数中,原来的训练目标最小化训练标签上的预测损失, 调整为最小化预测损失和惩罚项之和,以此使权重向量变小。新的损失函数 $C$ 如下:
\[C(\mathbf{w},b) = L(\mathbf{w}, b) + \frac{\lambda}{2} \|\mathbf{w}\|^2\]其中 $\lambda$ 为正则化常数。
使用随机梯度最小化损失函数,计算梯度得:
\[\frac{\partial C}{\partial w} = \frac{\partial C_0}{\partial w} + \frac{\lambda}{n} w\] \[\frac{\partial C}{\partial b} = \frac{\partial C_0}{\partial b}\]更新参数如下:
\[w \rightarrow w-\eta \frac{\partial C_0}{\partial w}-\frac{\eta \lambda}{n} w = \left(1-\frac{\eta \lambda}{n}\right) w -\eta \frac{\partial C_0}{\partial w}\]可看出 $w$ 每次都乘以小于 1 的系数 $(1-\frac{\eta \lambda}{n})$,逐渐衰减。
如果采用 $L1$ 范数,损失函数如下:
\[C(\mathbf{w},b) = L(\mathbf{w}, b) + \frac{\lambda}{n} \sum_w |w|\]求解梯度得:
\[\frac{\partial C}{\partial w} = \frac{\partial C_0}{\partial w} + \frac{\lambda}{n} \, {\rm sgn}(w)\]其中 ${\rm sgn}(w)$ 为 $w$ 的正负符号。
更新参数如下:
\[w \rightarrow w' = w-\frac{\eta \lambda}{n} {sgn}(w) - \eta\frac{\partial C_0}{\partial w}\]可以看出 $L1$ 正则使参数 $w$ 朝着 0 以常数逐渐衰减。
使用 $L2$ 范数的一个原因是权重向量的大分量惩罚更大。 这使得算法偏向于在大量特征上均匀分布权重的模型。 在实践中,这可能使它们对单个变量中的观测误差更为稳定。 相比之下,$L1$ 惩罚会导致模型将权重集中在一小部分特征上, 而将其他权重清除为零。 这称为特征选择(feature selection),这可能是其他场景下需要的。
Dropout
经典泛化理论认为,为了缩小训练和测试性能之间的差距,应该以简单的模型为目标。 参数的范数可以是模型简单性的一种度量。除此之外,简单性的另一个角度是平滑性,即函数不应该对其输入的微小变化敏感。 例如,当我们对图像进行分类时,我们预计向像素添加一些随机噪声应该是基本无影响的。
暂退法(dropout)在前向传播过程中同时注入噪声,这已经成为训练神经网络的常用技术。 之所以被称为暂退法,因为从表面上看是在训练过程中丢弃(drop out)一些神经元。 在整个训练过程的每一次迭代中,标准暂退法包括在计算下一层之前将当前层中的一些节点置零。
关键的挑战就是如何注入这种噪声。 一种想法是以一种无偏向(unbiased)的方式注入噪声。 这样在固定住其他层时,每一层的期望值等于没有噪音时的值。
在标准暂退法正则化中,通过按保留(未丢弃)的节点的分数进行规范化来消除每一层的偏差。 换言之,每个中间活性值 $h$ 以暂退概率 $p$ 由随机变量 $h’$ 替换,如下所示:
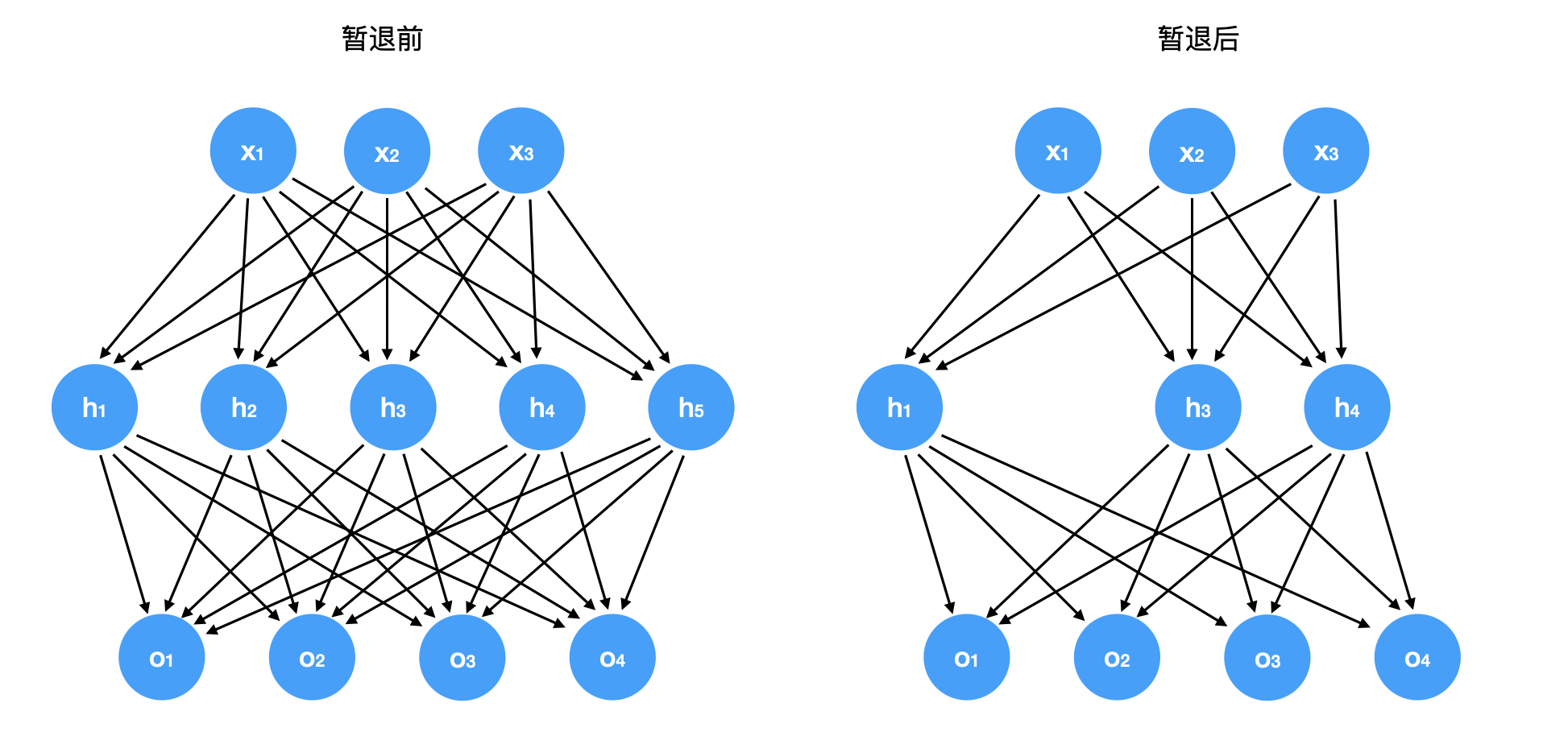
\[\begin{aligned} h' = \begin{cases} 0 & \text{ 概率为 } p \\ \frac{h}{1-p} & \text{ 其他情况} \end{cases} \end{aligned}\]当我们将暂退法应用到隐藏层,以 $p$ 的概率将隐藏单元置为零时, 结果可以看作是一个只包含原始神经元子集的网络。删除了 $h_2$ 和 $h_5$, 因此输出的计算不再依赖于 $h_2$ 或 $h_5$,并且它们各自的梯度在执行反向传播时也会消失。 这样输出层的计算不会过度依赖于 $h_1, \ldots, h_5$ 的任何一个元素。
通常在测试时不用暂退法。给定一个训练好的模型,不会丢弃任何节点。