多层神经网络基于梯度训练时容易出现训练不稳定。比如下图:
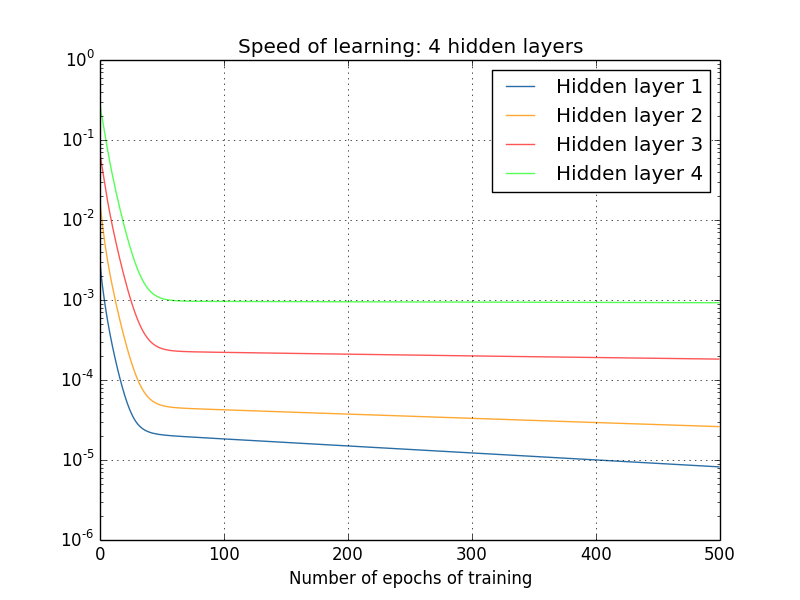
第一层参数的学习速度比最后一层慢了 100 倍以上,这意味着梯度回传过程中越来越小,靠前的神经网络训练比靠后的慢,这个现象称为梯度消失。由于我们网络参数是随机生成的,如果第一层训练不好,意味着很多信息在第一层就丢失了,即使后面几层训练得很好,模型也无法达到预期。
此外,也可能出现梯度在回传过程中越来越大,这种现象称为梯度爆炸。梯度在回传的过程中很不稳定,是多层神经网络难以训练的原因。
梯度分析
以下图的神经网络为例:

第 $j$ 个神经元的输出 $a_j$ 等于 $\sigma(z_j)$,其中 $z_j=w_ja_{j-1} + b_j)$。$C$ 为神经网络输出 $a_4$ 的函数。如果网络输出接近预期的输出,则 $C$ 很小,否则很大。
可得 $C$ 关于 $b_1$ 的偏导为:
\[\frac{\partial C}{\partial b_1}=\sigma'(z_1)\times w_2 \times \sigma'(z_2) \times w_3 \times \sigma'(z_3) \times w_4 \times \sigma'(z_4) \times \frac{\partial C}{\partial a_4}\]公式推导
如果 $b_1$ 微调了 $\Delta b_1$,相应的会导致第一层网络输出微调了 $\Delta a_1$,引起第二层神经网络的输入变化了 $\Delta z_2$,输出变化 $\Delta a_2$,以此类推 C 变化了 $\Delta C$。当 $\Delta b_1$ 足够小,可得:
\[\frac{\partial C}{\partial b_1}\approx \frac{\Delta C}{\Delta b_1}\]因此只需要计算出 $\frac{\Delta C}{\Delta b_1}$就能近似估算 $\frac{\partial C}{\partial b_1}$。
由 $a_1=\sigma(z_1)=\sigma(w_1 a_0 + b_1)$,可得:
\[\begin{aligned}\Delta a_1 & \approx \frac{\partial\sigma(w_1 a_0+b_1)}{\partial b_1}\Delta b_1 \\ & = \sigma'(z_1)\Delta b_1 \end{aligned}\]这一步推导出 $b_1$ 变化了 $\Delta b_1$ 引发 $a_1$ 变化了 $\Delta a_1$。
由 $z_2 = w_2 a_1 + b _2$ 可得:
\[\begin{aligned}\Delta z_2 & \approx \frac{\partial z_2}{\partial a_1}\Delta a_1 \\ &=w_2\Delta a_1\end{aligned}\]这一步推导出 $a_1$ 变化了 $\Delta a_1$ 引发 $z_2$ 变化了 $\Delta z_2$。
从上面两式可得:$\Delta z_2 \approx \sigma’(z_1)w_2\Delta b_1$。以此类推,可得
\[\Delta C \approx \sigma'(z_1)w_2\sigma'(z_2)...\sigma'(z_4)\frac{\partial C}{\partial a_4} \Delta b_1\]即
\[\frac{\partial C}{\partial b_1} = \sigma'(z_1)w_2\sigma'(z_2)...w_4\sigma'(z_4)\frac{\partial C}{\partial a_4}\]从上式可以看出,每多一层,梯度就会多乘一次 $\sigma’$。而如果采用的是 sigmod 激活函数,其导数最大值是 0.25。如果我们采用均值为 $0$ 标准差为 $1$ 的高斯分布随机初始化参数,则 $|w| < 1$。因此 $|w\sigma’|<1/4$,意味着每多一层,回传到第一层的梯度都会乘以小于 1/4 的值,导致梯度越来越小。
想规避梯度消失,需要满足 $|w\sigma’| \geq 1$。而使用 sigmoid 很难满足 $|w\sigma’| \geq 1$,因为如果 $w$ 取得很大,则 $\sigma’(z)=\sigma’(wa+b)$ 的值会变得很小(从 sigmoid 的导数图可以看出)。 这也是为什么现在更多使用 ReLu 作为激活函数。
随着训练进行,参数 $w$ 可能会越来越大,有可能不再满足 $|w\sigma’|<1/4$,甚至可能出现 $|w\sigma’| > 1$,则可能会引起梯度爆炸。
可以看出,无论是梯度消失还是梯度爆炸,本质原因都是因为梯度连乘导致无法保证每一层都以同样的速度进行参数更新。