优化挑战
深度学习优化存在许多挑战,例如局部最小值、鞍点和梯度消失。
局部最小值
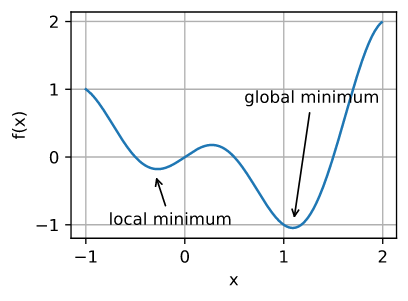
目标函数通常有许多局部最优解。当数值解接近局部最优值时,梯度接近或变为零,迭代得到的解可能是局部最优,而不是全局最优。
鞍点
鞍点(saddle point)是指函数的所有梯度都消失但既不是全局最小值也不是局部最小值。比如函数 $f(x)=x^3$:
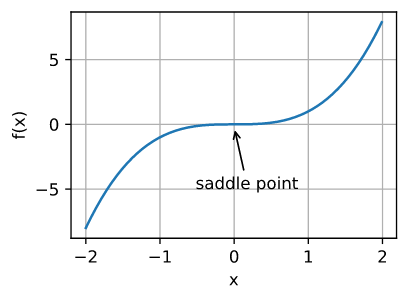
梯度消失
见上一篇文章《数值稳定性》。
优化算法
随机梯度下降 Stochastic Gradient Descent
标准梯度下降算法有两个缺点:
- 需要全量数据来计算参数更新,当数据集过大时无法放在内存中,影响效率
- 难以支持 online 模式更新,新数据无法很好的融合
Stochastic Gradient Descent(SGD)很好的解决了这两个问题。SGD 只需要少量甚至单个训练样本就可以更新参数。实践中通常采用小批量训练样本来更新参数,而不是单个样本。好处在于:
- 减少方差,更加稳定
- 能利用矩阵计算提高计算效率
使用 SGD 最好随机打乱训练样本:
One final but important point regarding SGD is the order in which we present the data to the algorithm. If the data is given in some meaningful order, this can bias the gradient and lead to poor convergence. Generally a good method to avoid this is to randomly shuffle the data prior to each epoch of training.
动量法
考虑函数 $f(\mathbf{x}) = 0.1x_1^2 + 2x_2^2$ ,执行梯度下降,可得:
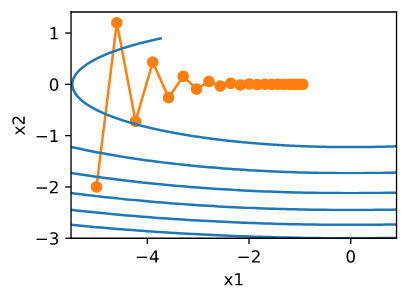
可以看出 $x_2$ 方向的梯度比水平 $x_1$ 方向的梯度大得多,变化也快得多。 如果选择较小的学习率,能确保不会在 $x_2$ 方向发散,但会导致 $x_1$ 方向缓慢收敛。如果学习率较高,在 $x_1$ 方向上可以很快收敛,但在 $x_2$ 方向将会发散。
动量法(momentum)能够解决上面描述的梯度下降问题。 观察上面的优化轨迹,如果梯度的计算考虑了历史的梯度值,效果会更好。 在 $x_1$ 方向上,梯度方向始终一致,梯度值会逐渐增大。在 $x_2$ 方向,梯度方向来回震荡,梯度值被相互抵消以致变小。
定义小批量随机梯度下降计算的梯度为 $\mathbf{g}$,则第 $t$ 次迭代梯度为:
\[\mathbf{g_t} = \partial_{\mathbf{w}} \frac{1}{|\mathcal{B_t}|} \sum_{i \in \mathcal{B}\_t} f(\mathbf{x_i}, \mathbf{w_{t-1}})\]动量法不采用 $\mathbf{g}_t$ 作为梯度值直接更新参数,而是采用动量 $\mathbf{v}_t$ 作为梯度值来更新参数。$\mathbf{v}_t$ 的计算公式为:
\[\mathbf{v}_t = \beta \mathbf{v}_{t-1} + \mathbf{g}_{t}\]其中 $\beta \in (0, 1)$。可以看出,动量法用多个过去梯度的加权平均值来替代瞬时梯度。相应的,参数更新的公式变成:
\[\mathbf{w}_t \leftarrow \mathbf{w}_{t-1} - \eta \mathbf{v}_t\]前面提到,梯度下降法可能会停滞到平原(梯度消失)、鞍点和局部最优点,因此带动量的梯度下降法能依靠之前的梯度值,冲过平原、鞍点和局部最优点,提高泛化性。
采用动量法,参数更新方向不仅由当前的梯度决定,也与此前累积的下降方向有关。这使得参数中那些梯度方向变化不大的维度可以加速更新,梯度方向变化较大的维度则减少更新幅度。由此起到加速收敛和减小震荡的效果。
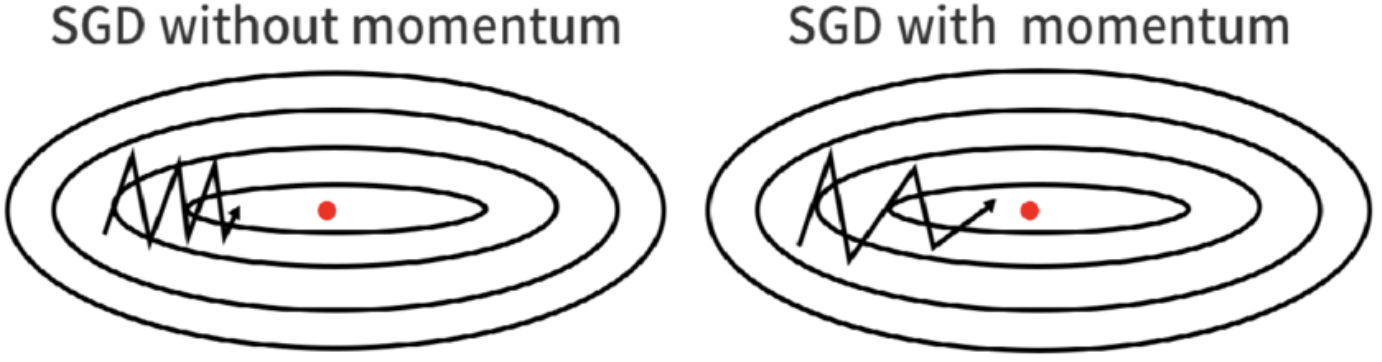
AdaGrad算法
在稀疏特征的模型训练时,固定的学习率会带来问题。常见的特征的参数一般都能快速收敛到最佳值,而对于不常见的特征,其相关参数训练的机会太少,收敛速度太慢。我们希望针对特征出现的频率来动态调整学习率。
解决此问题的一个方法是记录特定特征出现次数,然后将其用作调整学习率。
AdaGrad 算法通过采用先前观察所得梯度的平方之和作为特征计数器来解决这个问题。定义 $\mathbf{s}_t$ 来累加过去的梯度方差:
\[\begin{aligned}\mathbf{g}_t & = \partial_{\mathbf{w}} l(y_t, f(\mathbf{x_t},\mathbf{w})), \\ \mathbf{s}_t & = \mathbf{s}_{t-1} + \mathbf{g}_t^2, \\ \mathbf{w}_t & = \mathbf{w}_{t-1} - \frac{\eta}{\sqrt{\mathbf{s}_t + \epsilon}} \cdot \mathbf{g}_t \end{aligned}\]分母加上 $\epsilon$ 是为了避免除零异常。当训练前期梯度较小的时候,$\mathbf{s}_t$ 较小,能放大学习率。训练后期随着 $\mathbf{s}_t$ 增大,学习率逐渐下降。
RMSProp
Adagrad 算法将梯度 $\mathbf{g}_t$ 的平方累加成状态矢量 $\mathbf{s}_t = \mathbf{s}_{t-1} + \mathbf{g}_t^2$。 $\mathbf{s}_t$ 会持续增长,几乎上随着算法收敛线性递增。RMSProp 算法采用了类似动量法的做法,即 $\mathbf{s}_t \leftarrow \gamma \mathbf{s}_{t-1} + (1-\gamma) \mathbf{g}_t^2$。
Adam
Adam 算法是将动量法和 AdaGrad 融合而成。Adam 使用指数加权移动平均值来估算梯度的动量和二阶矩(second moment):
\[\begin{aligned} \mathbf{v}_t & \leftarrow \beta_1 \mathbf{v}_{t-1} + (1 - \beta_1) \mathbf{g}_t, \\ \mathbf{s}_t & \leftarrow \beta_2 \mathbf{s}_{t-1} + (1 - \beta_2) \mathbf{g}_t^2 \end{aligned}\]这里 $\beta_1$ 和 $\beta_2$ 是非负加权参数。 常将它们设置为 $\beta_1 = 0.9$ 和 $\beta_2 = 0.999$,梯度方差的更新远比动量慢。
如果初始化 $\mathbf{v}_0$ 和 $\mathbf{s}_0$ 为 $0$,则训练初期会带来很大的偏差,($\mathbf{v}_1 = 0.1 \mathbf{g}_1$,$\mathbf{s}_1 = 0.001 \mathbf{g}^2_1$)。因此需要对 $\mathbf{v}$ 和 $\mathbf{s}$ 做偏差纠正,定义 $\mathbf{\hat{v}}_t$ 和 $\mathbf{\hat{s}}_t$ 如下:
\[\hat{\mathbf{v}}_t = \frac{\mathbf{v}_t}{1 - \beta_1^t}\] \[\hat{\mathbf{s}}_t = \frac{\mathbf{s}_t}{1 - \beta_2^t}\]类似 RMSProp 算法,定义 $\mathbf{g’}$ 如下:
\[\mathbf{g}_t' = \frac{\eta \hat{\mathbf{v}}_t}{\sqrt{\hat{\mathbf{s}}_t} + \epsilon}\]通常取 $\epsilon = 10^{-6}$。最后,通过 $\mathbf{g’}$ 来更新参数:
\[\mathbf{w}_t \leftarrow \mathbf{w}_{t-1} - \mathbf{g}_t'\]